3.4.2 相似三角形的性质-2---同步课件 2021-2022学年湘教版数学九年级上册(共17张ppt)
文档属性
| 名称 | 3.4.2 相似三角形的性质-2---同步课件 2021-2022学年湘教版数学九年级上册(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 291.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 18:46:29 | ||
图片预览





文档简介
第三章 图形的相似
3.4.2 相似三角形的性质
第2课时 与相似三角形的周长、面积有关的性质
1、相似三角形对应角相等
2、相似三角形对应边成比例
3、相似三角形对应高的比等于相似比.
5、相似三角形对应中线的比等于相似比.
4、相似三角形对应角平分线的比等于相似比.
C′
C
A
B
A′
B′
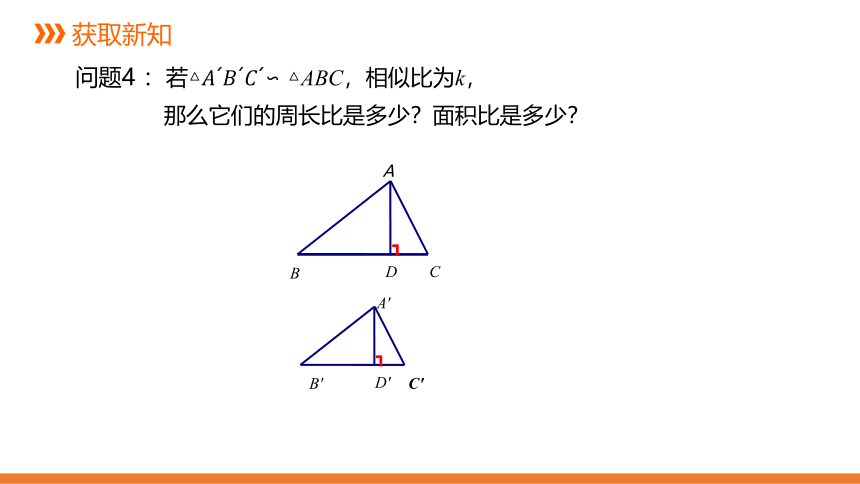
问题4 :若△ A’B’C’∽△ABC,相似比为k,
那么它们的周长比是多少?面积比是多少?
C′
C
A
B
A′
B′
因为 ,
所以
从而
的周长
的周长
C′
C
A
B
A′
B′
┓
┓
D′
D
问题4 :若△???????????????∽ △ABC,相似比为k,
那么它们的周长比是多少?面积比是多少?
?
C′
C
A
B
A′
B′
┓
┓
D′
D
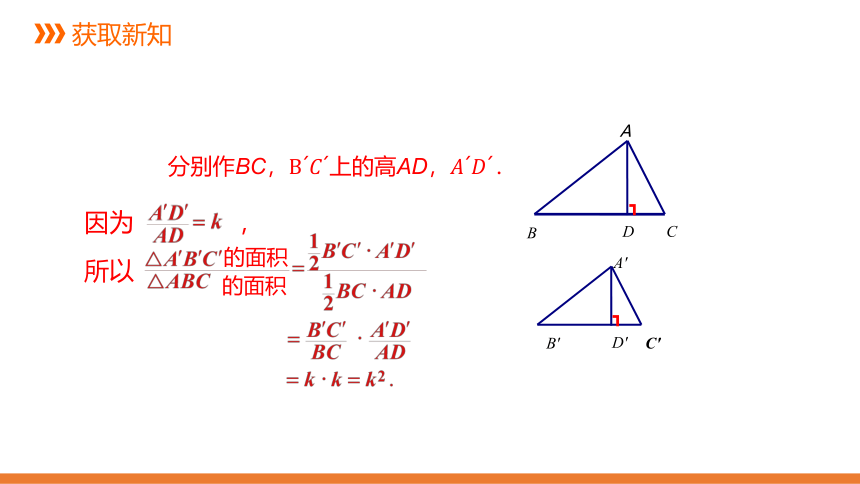
分别作BC,B??????上的高AD,??????????.
?
因为 ,
所以
的面积
的面积
相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方.
例2:在△ABC中,EF//BC,????????????????=12,????四边形????????????????=8.
?
A
C
B
E
F
求????△????????????.
?
A
C
B
E
F
又 S △ABC+ S △A ′ B ′ C ′ =91
∴ S △A ′ B ′ C ′ =63
1.相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______.
3∶5
3∶5
3∶5
9∶25
3∶5
2.已知两个相似多边形的相似比是4:5,周长的和是18cm,则两个多边形的周长分别是_________________.
8cm,10cm
1:4
3.如图:在△ABC中,M、N分别是AB、AC的中点,
(1)△AMN与△ABC的面积比是____;
A
B
C
N
M
(2)△AMN与四边形MNCB的面积
比是_________.
1:3
4.如图,DF∥EG∥BC,AD=DE=EB,则△ABC被分成的三部分的面积比S1:S2:S3为_______.
S3
B
E
D
F
G
C
S2
A
S1
5
3
:
1
:
全等三角形
相似三角形
对应边相等
对应边的比等于相似比
对应角相等
对应角相等
周长相等
周长的比等于相似比
面积相等
面积的比等于相似比的平方
对应高相等
对应高的比等于相似比
对应中线相等
对应中线的比等于相似比
对应角平分线相等
对应角平分线的比等于相似比
相似三角形的性质
3.4.2 相似三角形的性质
第2课时 与相似三角形的周长、面积有关的性质
1、相似三角形对应角相等
2、相似三角形对应边成比例
3、相似三角形对应高的比等于相似比.
5、相似三角形对应中线的比等于相似比.
4、相似三角形对应角平分线的比等于相似比.
C′
C
A
B
A′
B′
问题4 :若△ A’B’C’∽△ABC,相似比为k,
那么它们的周长比是多少?面积比是多少?
C′
C
A
B
A′
B′
因为 ,
所以
从而
的周长
的周长
C′
C
A
B
A′
B′
┓
┓
D′
D
问题4 :若△???????????????∽ △ABC,相似比为k,
那么它们的周长比是多少?面积比是多少?
?
C′
C
A
B
A′
B′
┓
┓
D′
D
分别作BC,B??????上的高AD,??????????.
?
因为 ,
所以
的面积
的面积
相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方.
例2:在△ABC中,EF//BC,????????????????=12,????四边形????????????????=8.
?
A
C
B
E
F
求????△????????????.
?
A
C
B
E
F
又 S △ABC+ S △A ′ B ′ C ′ =91
∴ S △A ′ B ′ C ′ =63
1.相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______.
3∶5
3∶5
3∶5
9∶25
3∶5
2.已知两个相似多边形的相似比是4:5,周长的和是18cm,则两个多边形的周长分别是_________________.
8cm,10cm
1:4
3.如图:在△ABC中,M、N分别是AB、AC的中点,
(1)△AMN与△ABC的面积比是____;
A
B
C
N
M
(2)△AMN与四边形MNCB的面积
比是_________.
1:3
4.如图,DF∥EG∥BC,AD=DE=EB,则△ABC被分成的三部分的面积比S1:S2:S3为_______.
S3
B
E
D
F
G
C
S2
A
S1
5
3
:
1
:
全等三角形
相似三角形
对应边相等
对应边的比等于相似比
对应角相等
对应角相等
周长相等
周长的比等于相似比
面积相等
面积的比等于相似比的平方
对应高相等
对应高的比等于相似比
对应中线相等
对应中线的比等于相似比
对应角平分线相等
对应角平分线的比等于相似比
相似三角形的性质
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
