人教版八年级数学上册:11.1.2 三角形的角平分线 11.1.3 三角形稳定性 课件(共17张ppt)
文档属性
| 名称 | 人教版八年级数学上册:11.1.2 三角形的角平分线 11.1.3 三角形稳定性 课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 18:50:17 | ||
图片预览




文档简介
O
A
B
C
D
E
F
C
A
B
D
A
B
C
D
E
F
O
回顾旧知
●
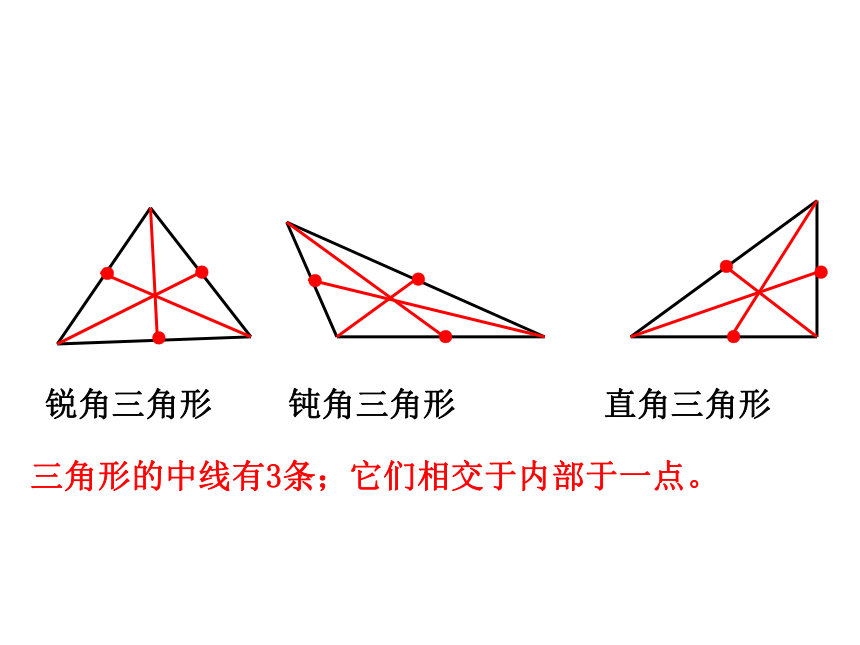
三角形的中线有3条;它们相交于内部于一点。
●
●
●
●
●
●
●
●
锐角三角形
钝角三角形
直角三角形
∠ABC
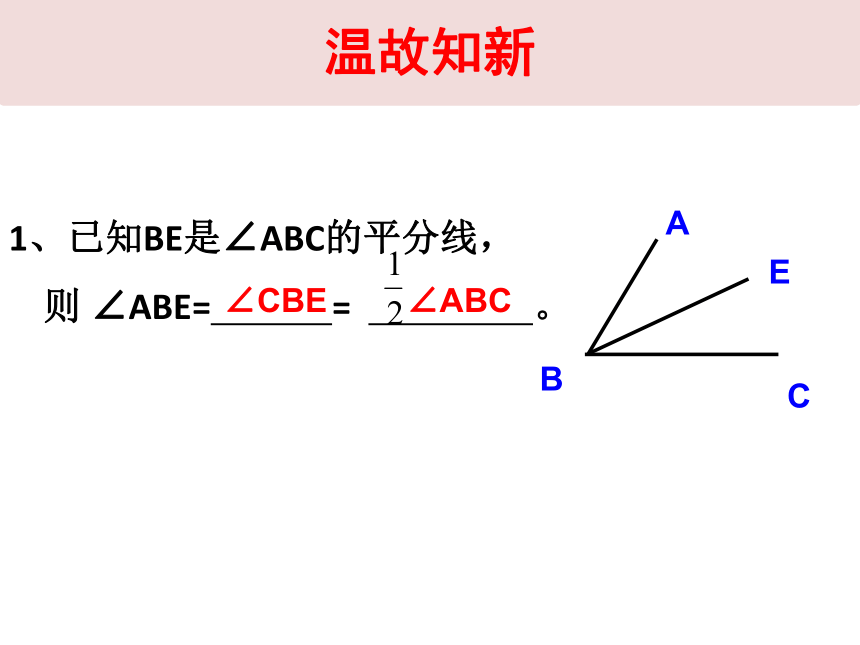
1、已知BE是∠ABC的平分线,
则 ∠ABE= = 。
A
C
B
E
∠CBE
温故知新
11.1.2三角形的角平分线
11.1.3三角形稳定性
学习目标(1分钟)
1、掌握三角形中角平分线的概念;
2、了解三角形的稳定性在日常生活中的应用.
自学指导一(5分钟)
认真阅读课本第5页,思考下列问题:
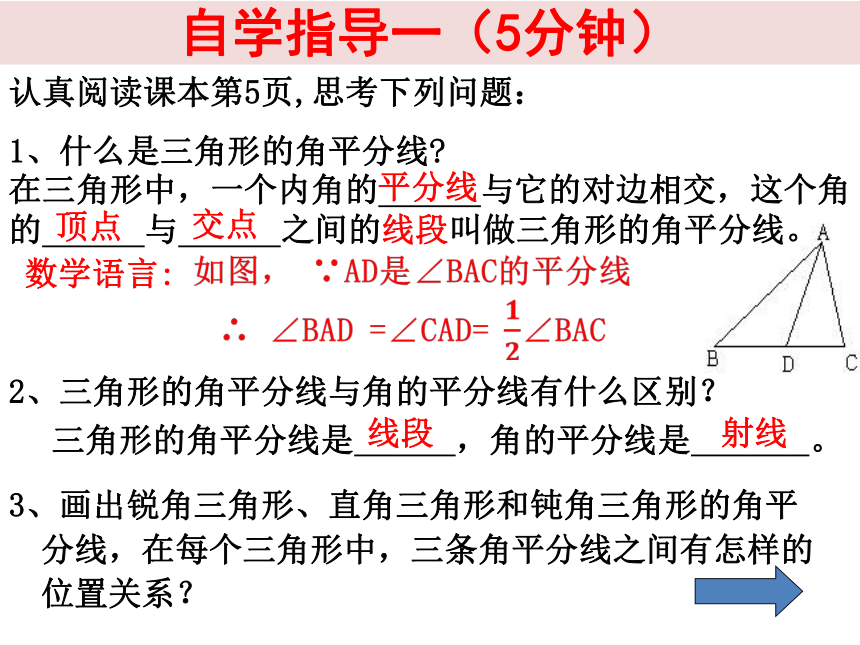
1、什么是三角形的角平分线?
2、三角形的角平分线与角的平分线有什么区别?
3、画出锐角三角形、直角三角形和钝角三角形的角平分线,在每个三角形中,三条角平分线之间有怎样的位置关系?
三角形的角平分线是 ,角的平分线是 。
?
数学语言:
线段
射线
在三角形中,一个内角的 与它的对边相交,这个角的 与 之间的线段叫做三角形的角平分线。
平分线
顶点
交点
∴∠ABE=_____ = _____
∵BE是△ABC的角平分线
∴∠ACB=2______=2______
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
自学检测一(5分钟)
1、填空(如图1)
2、三角形的三条角平分线的交点在三角形的( )
A.内部 B.外部 C.一条边上 D.都可能
3、如图2,AE是 △ABC的角平分线,
已知 ∠B=45°,∠C=60°,
求∠BAE和∠AEC的度数 .
C
A
B
E
图2
A
C
B
F
E
O
图1
A
解析:欲求∠BAE必须先求∠BAC,由三角形的内角和定理可求∠BAC,再由角平分线的性质就可求∠BAE;因为∠CAE=∠BAE,由三角形的内角和定理可求∠AEC
3、如图,AE是 △ABC的角平分线,已知 ∠B=45°
∠C=60°,求∠BAE和∠AEC的度数。
∵AE是△ABC的角平分线
解:∵∠BAC+∠B+∠C=1800
∴∠BAE=∠CAE= ∠BAC=
( )
∴∠BAC=1800-∠B-∠C=1800-450-600=750
三角形的内角和定理
C
A
B
E
∵∠AEC+∠CAE+∠C=1800
∴∠AEC=1800-∠C-∠CAE=1800-600-37.50=82.50
点拨运用(3分钟)
( )
三角形的内角和定理
盖房子时,在窗框未安装好之前,木工师傅常常现在窗框上斜钉一根木条.为什么要这样做?
三角形
具有稳定性,
四边形
不具有稳定性.
自学指导二(2分钟)
1、下列图形中具有稳定性的是( )
(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形
2、要使下列木架稳定各至少需要多少根木棍?
C
自学检测二(5分钟)
1.三角形的角平分线.
2.三角形的稳定性.
通过本课时的学习,你收获了什么呢?
课堂小结(2分钟)
1、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
B
2、下列图形中哪些具有稳定性?
√
√
√
×
×
×
当堂训练(15分钟)
3.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是△ABE的角平分线( )
②BE是△ ABD边AD上的中线( )
③BE是△ ABC边AC上的中线( )
④CH是△ ACD边AD上的高( )
×
×
×
√
(选做题)△ABC中∠BAC=500,∠ABC和∠ACB的 平分线交于O点,连接AO,则∠BOC的度数.
1
2
A
B
C
O
解:∵ ∠ABC+ ∠ACB+ ∠BAC=180°
∠BAC=50°
∴ ∠ABC+ ∠ACB=130°
∵OB,OC分别是∠ABC和∠ACB的 平分线
∴ ∠BOC=180°-( ∠1+ ∠2 )
=180°-65°
=115°
作业布置
1.课本P8复习巩固第8题(作业本)
2.继续试卷第2页
3.预习课本P11-14
板书设计
1、三角形的角平分线:
三角形的三条角平分线相交于一点,交点在三角形的内部.
2、三角形具有稳定性
根据下列完成课本第8页复习巩固第三题
(1) 你能分别画出这三个三角形的三条角平分线吗?
做一做
(2) 在每个三角形中,这三条角平分线之间有怎样的位置关系?将你的结果与同伴交流。
解:三角形的三条角平分线交于内部同一点.
A
B
C
D
E
F
C
A
B
D
A
B
C
D
E
F
O
回顾旧知
●
三角形的中线有3条;它们相交于内部于一点。
●
●
●
●
●
●
●
●
锐角三角形
钝角三角形
直角三角形
∠ABC
1、已知BE是∠ABC的平分线,
则 ∠ABE= = 。
A
C
B
E
∠CBE
温故知新
11.1.2三角形的角平分线
11.1.3三角形稳定性
学习目标(1分钟)
1、掌握三角形中角平分线的概念;
2、了解三角形的稳定性在日常生活中的应用.
自学指导一(5分钟)
认真阅读课本第5页,思考下列问题:
1、什么是三角形的角平分线?
2、三角形的角平分线与角的平分线有什么区别?
3、画出锐角三角形、直角三角形和钝角三角形的角平分线,在每个三角形中,三条角平分线之间有怎样的位置关系?
三角形的角平分线是 ,角的平分线是 。
?
数学语言:
线段
射线
在三角形中,一个内角的 与它的对边相交,这个角的 与 之间的线段叫做三角形的角平分线。
平分线
顶点
交点
∴∠ABE=_____ = _____
∵BE是△ABC的角平分线
∴∠ACB=2______=2______
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
自学检测一(5分钟)
1、填空(如图1)
2、三角形的三条角平分线的交点在三角形的( )
A.内部 B.外部 C.一条边上 D.都可能
3、如图2,AE是 △ABC的角平分线,
已知 ∠B=45°,∠C=60°,
求∠BAE和∠AEC的度数 .
C
A
B
E
图2
A
C
B
F
E
O
图1
A
解析:欲求∠BAE必须先求∠BAC,由三角形的内角和定理可求∠BAC,再由角平分线的性质就可求∠BAE;因为∠CAE=∠BAE,由三角形的内角和定理可求∠AEC
3、如图,AE是 △ABC的角平分线,已知 ∠B=45°
∠C=60°,求∠BAE和∠AEC的度数。
∵AE是△ABC的角平分线
解:∵∠BAC+∠B+∠C=1800
∴∠BAE=∠CAE= ∠BAC=
( )
∴∠BAC=1800-∠B-∠C=1800-450-600=750
三角形的内角和定理
C
A
B
E
∵∠AEC+∠CAE+∠C=1800
∴∠AEC=1800-∠C-∠CAE=1800-600-37.50=82.50
点拨运用(3分钟)
( )
三角形的内角和定理
盖房子时,在窗框未安装好之前,木工师傅常常现在窗框上斜钉一根木条.为什么要这样做?
三角形
具有稳定性,
四边形
不具有稳定性.
自学指导二(2分钟)
1、下列图形中具有稳定性的是( )
(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形
2、要使下列木架稳定各至少需要多少根木棍?
C
自学检测二(5分钟)
1.三角形的角平分线.
2.三角形的稳定性.
通过本课时的学习,你收获了什么呢?
课堂小结(2分钟)
1、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
B
2、下列图形中哪些具有稳定性?
√
√
√
×
×
×
当堂训练(15分钟)
3.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是△ABE的角平分线( )
②BE是△ ABD边AD上的中线( )
③BE是△ ABC边AC上的中线( )
④CH是△ ACD边AD上的高( )
×
×
×
√
(选做题)△ABC中∠BAC=500,∠ABC和∠ACB的 平分线交于O点,连接AO,则∠BOC的度数.
1
2
A
B
C
O
解:∵ ∠ABC+ ∠ACB+ ∠BAC=180°
∠BAC=50°
∴ ∠ABC+ ∠ACB=130°
∵OB,OC分别是∠ABC和∠ACB的 平分线
∴ ∠BOC=180°-( ∠1+ ∠2 )
=180°-65°
=115°
作业布置
1.课本P8复习巩固第8题(作业本)
2.继续试卷第2页
3.预习课本P11-14
板书设计
1、三角形的角平分线:
三角形的三条角平分线相交于一点,交点在三角形的内部.
2、三角形具有稳定性
根据下列完成课本第8页复习巩固第三题
(1) 你能分别画出这三个三角形的三条角平分线吗?
做一做
(2) 在每个三角形中,这三条角平分线之间有怎样的位置关系?将你的结果与同伴交流。
解:三角形的三条角平分线交于内部同一点.
