2021-2022学年湘教版数学八年级上册4.5 一元一次不等式组---同步课件(22张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级上册4.5 一元一次不等式组---同步课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 18:46:18 | ||
图片预览








文档简介
4.5 一元一次不等式组
第四章 一元一次不等式(组)
情景引入
一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛.(注:用于国际比赛的足球场的长在100至110m之间,宽在64至75m之间.)
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像这样 这样,把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
特征:
1、同一个未知数
2、包含2个或2个以上的不等式
3、书写时不能漏掉边上的大括号
④
例题讲解
怎样确定不等式组中x的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
获取新知
2. 将第1题中各不等式的解集在同一条数轴上表示出来.
1. 分别解不等式
4. 与同学交流,怎样解一元一次不等式组.
3. 说出不等式组 的解集.
某数加上4就大于3,且这个数的一半与2的差是正数,你能列出有关这个数的不等式组吗?
解一元一次不等式组过程:
1、先解不等式组中的各个不等式,
2、然后求各个不等式解集的公共部分(常利用数轴),
3、用不等式表示公共部分,即求出了这个不等式组的解集.
在数轴上表示不等式的解集时应注意:
1、大于向右画,小于向左画;
2、有等号的画实心圆点,无等号的画空心圆圈.
注:如果没有公共部分,就说这个不等式组无解.
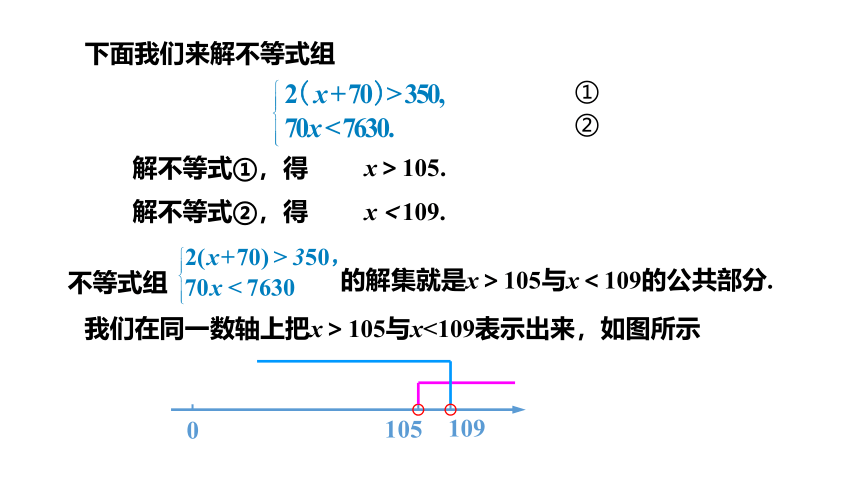
下面我们来解不等式组
解不等式①,得
解不等式②,得
①
②
x>105.
x<109.
的解集就是x>105与x<109的公共部分.
不等式组
我们在同一数轴上把x>105与x<109表示出来,如图所示
0
105
109
由图容易发现它们的公共部分是105<x <109,这就是由不等式①、②组成
的不等式组 的解集.
由此可知,这个足球场的长度在105至109m之间,从场地的大小方面来说,可以进行国际足球比赛.
例1 解不等式组:
解不等式①,得
解
x ≤ 3.
解不等式②,得
x <-3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是x<-3,所以这个不等式组的解集是x<-3.
例题讲解
例2 解不等式组:
解不等式①,得
解
x >-2.
解不等式②,得
x >6.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3 解不等式组:
解不等式①,得
解
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
3
由图可以看出这两个不等式的解集没有公共部分.这时,我们说这个不等式组无解.
利用数轴,求下列不等式组的解集口诀
∴这个不等式组的解集是x>1.
∴这个不等式组的解集是x<-2.
∴这个不等式组的解集是-2∴这个不等式组无解。
① x>1
x>-2
② x<1
x<-2
③ x>-2
x<1
④ x>1
x<-2
1
同大取大
同小取小
大小小大中间找
大大小小无解了
1. 填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
随堂演练
2. 解下列不等式方程组:
(1)答: 1<x<5.
(2)答: -4<x≤1
(3)答: x<
(4)答: 无解
3.关于x的不等式组 的整数解共有5个,求a的取值范围。
解析
∴不等式组的解集为a≤x<2.
由题意,此不等式组的整数解有五个,只能是-3,-2,-1,0,1.
∴a的取值范围为-4<a≤-3.
4. 若不等式组 有解,那么a必须满足 .
解析
由②得 ,因不等式组有解,
所以 ,故a>-2.
a>-2
5.不等式 的解集是 ,
解析
由①得x>-6,由②得x≤1,
所以不等式组的解集为-6-6 < x ≤ 1
6.不等式组 的解集是( ).
A.x>-1 B.x<3 C.-1C
解不等式x+1>0,得x>-1,
解不等式x-2<1,得x<3,
∴不等式组的解集为-1解析
7.k满足______时,方程组 中的x大于1,y小于1?
解析
由方程组加减消元得:
由题意得:
解得 -1<k<3
1. 不等式的基本性质有哪些?
2. 解一元一次不等式与解一元一次方程,有哪些相同之处和不同之处?
3. 应用一元一次不等式解决实际问题的一般步骤是什么?
4. 如何确定一元一次不等式组的解集?
课堂小结
第四章 一元一次不等式(组)
情景引入
一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛.(注:用于国际比赛的足球场的长在100至110m之间,宽在64至75m之间.)
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像这样 这样,把含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
特征:
1、同一个未知数
2、包含2个或2个以上的不等式
3、书写时不能漏掉边上的大括号
④
例题讲解
怎样确定不等式组中x的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
获取新知
2. 将第1题中各不等式的解集在同一条数轴上表示出来.
1. 分别解不等式
4. 与同学交流,怎样解一元一次不等式组.
3. 说出不等式组 的解集.
某数加上4就大于3,且这个数的一半与2的差是正数,你能列出有关这个数的不等式组吗?
解一元一次不等式组过程:
1、先解不等式组中的各个不等式,
2、然后求各个不等式解集的公共部分(常利用数轴),
3、用不等式表示公共部分,即求出了这个不等式组的解集.
在数轴上表示不等式的解集时应注意:
1、大于向右画,小于向左画;
2、有等号的画实心圆点,无等号的画空心圆圈.
注:如果没有公共部分,就说这个不等式组无解.
下面我们来解不等式组
解不等式①,得
解不等式②,得
①
②
x>105.
x<109.
的解集就是x>105与x<109的公共部分.
不等式组
我们在同一数轴上把x>105与x<109表示出来,如图所示
0
105
109
由图容易发现它们的公共部分是105<x <109,这就是由不等式①、②组成
的不等式组 的解集.
由此可知,这个足球场的长度在105至109m之间,从场地的大小方面来说,可以进行国际足球比赛.
例1 解不等式组:
解不等式①,得
解
x ≤ 3.
解不等式②,得
x <-3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是x<-3,所以这个不等式组的解集是x<-3.
例题讲解
例2 解不等式组:
解不等式①,得
解
x >-2.
解不等式②,得
x >6.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3 解不等式组:
解不等式①,得
解
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
3
由图可以看出这两个不等式的解集没有公共部分.这时,我们说这个不等式组无解.
利用数轴,求下列不等式组的解集口诀
∴这个不等式组的解集是x>1.
∴这个不等式组的解集是x<-2.
∴这个不等式组的解集是-2
① x>1
x>-2
② x<1
x<-2
③ x>-2
x<1
④ x>1
x<-2
1
同大取大
同小取小
大小小大中间找
大大小小无解了
1. 填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
随堂演练
2. 解下列不等式方程组:
(1)答: 1<x<5.
(2)答: -4<x≤1
(3)答: x<
(4)答: 无解
3.关于x的不等式组 的整数解共有5个,求a的取值范围。
解析
∴不等式组的解集为a≤x<2.
由题意,此不等式组的整数解有五个,只能是-3,-2,-1,0,1.
∴a的取值范围为-4<a≤-3.
4. 若不等式组 有解,那么a必须满足 .
解析
由②得 ,因不等式组有解,
所以 ,故a>-2.
a>-2
5.不等式 的解集是 ,
解析
由①得x>-6,由②得x≤1,
所以不等式组的解集为-6
6.不等式组 的解集是( ).
A.x>-1 B.x<3 C.-1
解不等式x+1>0,得x>-1,
解不等式x-2<1,得x<3,
∴不等式组的解集为-1
7.k满足______时,方程组 中的x大于1,y小于1?
解析
由方程组加减消元得:
由题意得:
解得 -1<k<3
1. 不等式的基本性质有哪些?
2. 解一元一次不等式与解一元一次方程,有哪些相同之处和不同之处?
3. 应用一元一次不等式解决实际问题的一般步骤是什么?
4. 如何确定一元一次不等式组的解集?
课堂小结
同课章节目录
