2021-2022学年湘教版数学八年级上册3.1第1课时平方根和算术平方根---同步课件(21张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级上册3.1第1课时平方根和算术平方根---同步课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览




文档简介
第三章 实数
3.1 第1课时 平方根和算术平方根
情景引入
某家庭在装修儿童房时需铺地垫10.8平方米,刚好用去正方形的地垫30块.你能算出每块地垫的边长是多少吗?
每块正方形地垫的面积是
10.8÷30=0.36(平方米)
即边长×边长= 0.36.
由于 ,
因此面积为0.36平方米的正方形地垫的边长是0.6米.
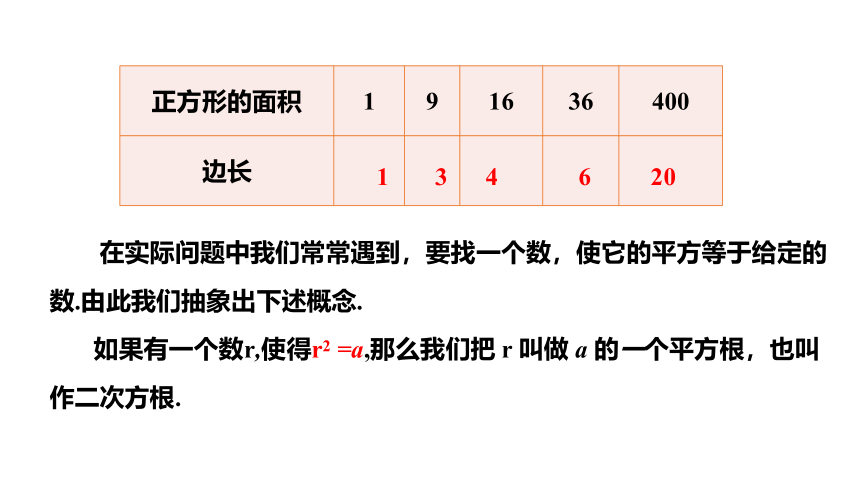
{8A107856-5554-42FB-B03E-39F5DBC370BA}正方形的面积
1
9
16
36
400
边长
在实际问题中我们常常遇到,要找一个数,使它的平方等于给定的数.由此我们抽象出下述概念.
如果有一个数r,使得r2 =a,那么我们把 r 叫做 a 的一个平方根,也叫作二次方根.
1
3
4
6
20
如果有一个数r,使得r2=a,那么我们把r叫作a的一个平方根,也叫作二次方根.
例如,22=4,则2是4的一个平方根
若 r2= a,则 r 是 a 的一个平方根.
获取新知
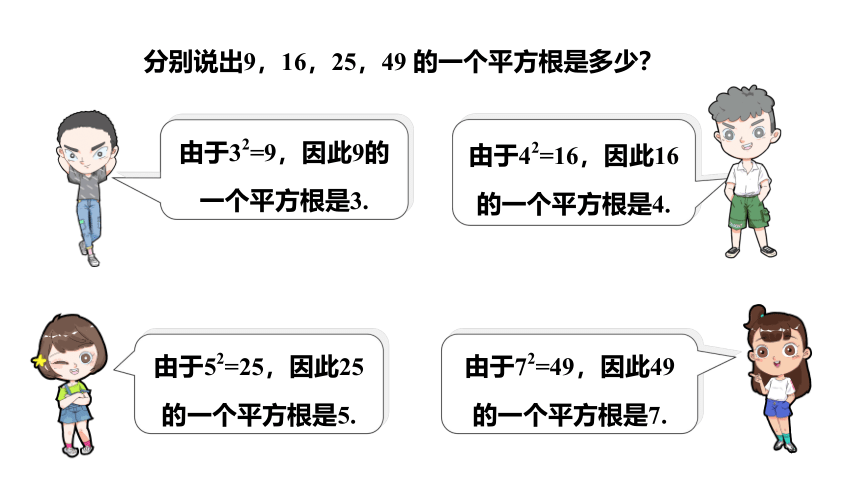
分别说出9,16,25,49 的一个平方根是多少?
由于32=9,因此9的一个平方根是3.
由于42=16,因此16的一个平方根是4.
由于52=25,因此25的一个平方根是5.
由于72=49,因此49的一个平方根是7.
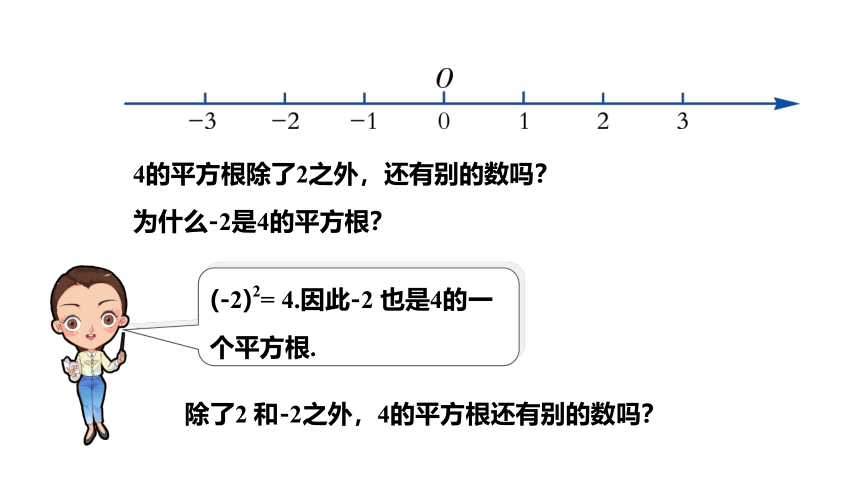
4的平方根除了2之外,还有别的数吗?
为什么-2是4的平方根?
(-2)2= 4.因此-2 也是4的一个平方根.
除了2 和-2之外,4的平方根还有别的数吗?
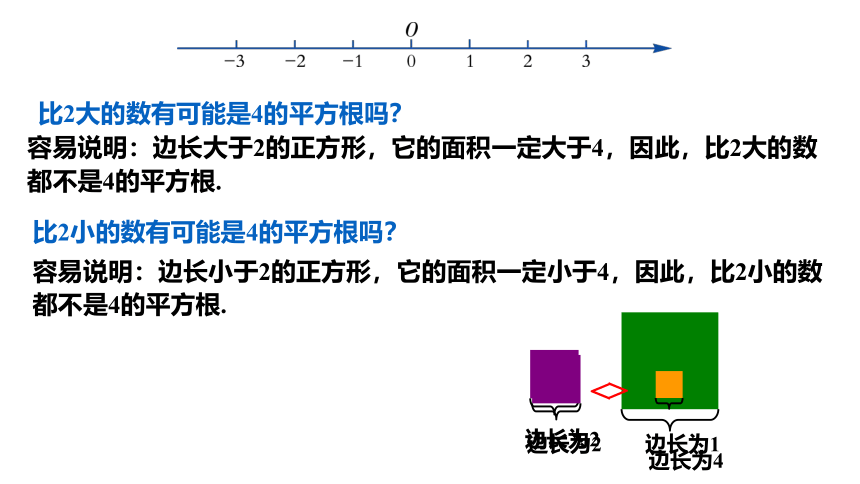
比2大的数有可能是4的平方根吗?
容易说明:边长大于2的正方形,它的面积一定大于4,因此,比2大的数都不是4的平方根.
边长为2
边长为4
<
比2小的数有可能是4的平方根吗?
边长为1
>
容易说明:边长小于2的正方形,它的面积一定小于4,因此,比2小的数都不是4的平方根.
边长为2
由于(-b)2=b2,因此由上述可知,-2以外的负数都不是4的平方根.
显然0不是4的平方根.
因此,4的平方根有且只有两个:2与-2.
如果r是正数a的一个平方根,那么a的平方根有且只有两个:r与-r.
我们把a的正平方根叫作a的算术平方根,记作 ,读作“根号a” (其中a ≥0);
这样正数a的平方根可以用符号“ ”来表示. 读作“正、负根号a” .
把a的负平方根记作 ,读作“负根号a” (其中a ≥ 0).
零的平方根是多少?负数有平方根吗?
由于同号两数相乘得正数,且02=0,因此负数没有平方根.
由于02=0,因此零的平方根就是0本身.我们把0的平方根也叫作0的算术平方根,记作 ,即 .
求一个非负数的平方根,叫作开平方.
开平方与平方互为逆运算,根据这种关系,可以求一个数的平方根.
+1
-1
+2
-2
+3
-3
1
4
9
开平方
平方
例1 分别求下列各数的平方根:
36, , 1.21.
由于62=36,
因此36的平方根是6与-6.
(1)36
即
36是正数
有两个平方根
例题讲解
(3)1.21
解
(2)
由于 2= ,
有两个平方根
因此 的平方根是 与 .
解
由于1.12=1.21,
有两个平方根
因此1.21的平方根是1.1与-1.1.
即
即
例2 分别求下列各数的算术平方根:
100, , 0.49.
解
由于102=100,
(1)100
算术平方根就是正平方根
因此 ;
解
(2)
由于 2= ,
算术平方根就是正平方根.
解
由于0.72=0.49,
(3)0.49
因此 ;
因此 .
1. 分别求 64, , 6.25 的平方根.
解:
由于82=64
所以64的平方根是8与-8.
由于
所以 的平方根是 与 .
由于2.52=6.25
所以6.25的平方根是2.5与-2.5.
随堂演练
2. 分别求 81, , 0.16 算术平方根.
解:
由于92=81
因此 .
由于0.42=0.16
因此 .
由于
因此 .
3. 判断下列说法是否正确.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
(4) 的平方根是-4 .
正确.
正确.
不正确,是4.
不正确,是±4.
4. 9的算术平方根是( ).
A.-3 B.3 C. ±3 D.81
B
解
因为32=9,所以9的算术平方根是3.
即 .
故,应选择B.
5. 4的平方根是 .
±2
解
因为(±2)2= 4,所以4的平方根是2.
即 .
故,答案是±2.
6.若2m-4与3m-1是同一个数的平方根,则m为( ).
A.-3 B.1 C.-3或1 D.-1
C
解
依题意,得(2m-4)+(3m-1)=0,解之,得m=1. 或2m-4=3m-1. 解之,得m=-3. 故应选择C.
根据平方根的性质,一个正数有两个平方根,且它们互为相反数,即(2m-4)+(3m-1)=0;而本题隐含一个条件,也就是说,2m-4与3m-1也可能是其中的一个平方根,即2m-4=3m-1.
分析
课堂小结
3.1 第1课时 平方根和算术平方根
情景引入
某家庭在装修儿童房时需铺地垫10.8平方米,刚好用去正方形的地垫30块.你能算出每块地垫的边长是多少吗?
每块正方形地垫的面积是
10.8÷30=0.36(平方米)
即边长×边长= 0.36.
由于 ,
因此面积为0.36平方米的正方形地垫的边长是0.6米.
{8A107856-5554-42FB-B03E-39F5DBC370BA}正方形的面积
1
9
16
36
400
边长
在实际问题中我们常常遇到,要找一个数,使它的平方等于给定的数.由此我们抽象出下述概念.
如果有一个数r,使得r2 =a,那么我们把 r 叫做 a 的一个平方根,也叫作二次方根.
1
3
4
6
20
如果有一个数r,使得r2=a,那么我们把r叫作a的一个平方根,也叫作二次方根.
例如,22=4,则2是4的一个平方根
若 r2= a,则 r 是 a 的一个平方根.
获取新知
分别说出9,16,25,49 的一个平方根是多少?
由于32=9,因此9的一个平方根是3.
由于42=16,因此16的一个平方根是4.
由于52=25,因此25的一个平方根是5.
由于72=49,因此49的一个平方根是7.
4的平方根除了2之外,还有别的数吗?
为什么-2是4的平方根?
(-2)2= 4.因此-2 也是4的一个平方根.
除了2 和-2之外,4的平方根还有别的数吗?
比2大的数有可能是4的平方根吗?
容易说明:边长大于2的正方形,它的面积一定大于4,因此,比2大的数都不是4的平方根.
边长为2
边长为4
<
比2小的数有可能是4的平方根吗?
边长为1
>
容易说明:边长小于2的正方形,它的面积一定小于4,因此,比2小的数都不是4的平方根.
边长为2
由于(-b)2=b2,因此由上述可知,-2以外的负数都不是4的平方根.
显然0不是4的平方根.
因此,4的平方根有且只有两个:2与-2.
如果r是正数a的一个平方根,那么a的平方根有且只有两个:r与-r.
我们把a的正平方根叫作a的算术平方根,记作 ,读作“根号a” (其中a ≥0);
这样正数a的平方根可以用符号“ ”来表示. 读作“正、负根号a” .
把a的负平方根记作 ,读作“负根号a” (其中a ≥ 0).
零的平方根是多少?负数有平方根吗?
由于同号两数相乘得正数,且02=0,因此负数没有平方根.
由于02=0,因此零的平方根就是0本身.我们把0的平方根也叫作0的算术平方根,记作 ,即 .
求一个非负数的平方根,叫作开平方.
开平方与平方互为逆运算,根据这种关系,可以求一个数的平方根.
+1
-1
+2
-2
+3
-3
1
4
9
开平方
平方
例1 分别求下列各数的平方根:
36, , 1.21.
由于62=36,
因此36的平方根是6与-6.
(1)36
即
36是正数
有两个平方根
例题讲解
(3)1.21
解
(2)
由于 2= ,
有两个平方根
因此 的平方根是 与 .
解
由于1.12=1.21,
有两个平方根
因此1.21的平方根是1.1与-1.1.
即
即
例2 分别求下列各数的算术平方根:
100, , 0.49.
解
由于102=100,
(1)100
算术平方根就是正平方根
因此 ;
解
(2)
由于 2= ,
算术平方根就是正平方根.
解
由于0.72=0.49,
(3)0.49
因此 ;
因此 .
1. 分别求 64, , 6.25 的平方根.
解:
由于82=64
所以64的平方根是8与-8.
由于
所以 的平方根是 与 .
由于2.52=6.25
所以6.25的平方根是2.5与-2.5.
随堂演练
2. 分别求 81, , 0.16 算术平方根.
解:
由于92=81
因此 .
由于0.42=0.16
因此 .
由于
因此 .
3. 判断下列说法是否正确.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
(4) 的平方根是-4 .
正确.
正确.
不正确,是4.
不正确,是±4.
4. 9的算术平方根是( ).
A.-3 B.3 C. ±3 D.81
B
解
因为32=9,所以9的算术平方根是3.
即 .
故,应选择B.
5. 4的平方根是 .
±2
解
因为(±2)2= 4,所以4的平方根是2.
即 .
故,答案是±2.
6.若2m-4与3m-1是同一个数的平方根,则m为( ).
A.-3 B.1 C.-3或1 D.-1
C
解
依题意,得(2m-4)+(3m-1)=0,解之,得m=1. 或2m-4=3m-1. 解之,得m=-3. 故应选择C.
根据平方根的性质,一个正数有两个平方根,且它们互为相反数,即(2m-4)+(3m-1)=0;而本题隐含一个条件,也就是说,2m-4与3m-1也可能是其中的一个平方根,即2m-4=3m-1.
分析
课堂小结
同课章节目录
