2.4 第2课时 线段垂直平分线、垂线的作法---同步课件 2021-2022学年湘教版数学八年级上册(共15张ppt)
文档属性
| 名称 | 2.4 第2课时 线段垂直平分线、垂线的作法---同步课件 2021-2022学年湘教版数学八年级上册(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 393.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览






文档简介
第二章 三角形
2.4 第2课时 线段垂直平分线、垂线的作法
知识回顾
二、逆定理(判定定理):
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线
一、性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
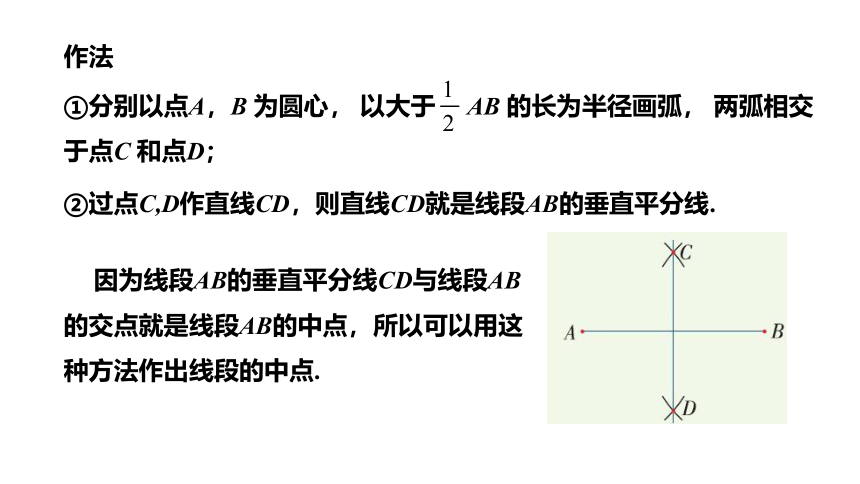
如图,已知线段AB,作线段AB 的垂直平分线.
根据“到线段两端距离相等的点在线段的垂直平分线上”,要作线段AB的垂直平分线,关键是找出到线段AB两端距离相等的两点.
获取新知
作法
①分别以点A,B 为圆心, 以大于 AB 的长为半径画弧, 两弧相交于点C 和点D;
②过点C,D作直线CD,则直线CD就是线段AB的垂直平分线.
因为线段AB的垂直平分线CD与线段AB的交点就是线段AB的中点,所以可以用这种方法作出线段的中点.
如何过一点P作已知直线l的垂线呢?
由于两点确定一条直线, 因此我们可以通过在已知直线上作线段的垂直平分线来找出垂线上的另一点,从而确定已知直线的垂线.
(1)当点P在直线l上.
(2)当点P在直线l外.
点P与已知直线l的位置关系有两种:
①在直线l 上点P 的两旁分别截取线段PA, PB,使PA= PB;
(1)当点P在直线l上.
②分别以A,B 为圆心 以大于 AB 的长为半径画弧, 两弧相交于点C;
③过点C, P作直线CP, 则直线CP为所求作的直线.
(2) 当点P在直线l外.
①以点P 为圆心, 以大于点P 到直线l的距离的线段长为半径画弧, 交直线l于点A,B;
②分别以A,B 为圆心 以大于 AB 的长为半径画弧, 两弧相交于点C;
③过点C,P作直线CP,则直线CP为所求作的直线.
例题讲解
线段的垂直平分线
一、性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
课堂小结
二、逆定理(判定定理):
到线段两个端点距离相等的点,在这条线段的垂直平分线上。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
课堂小结
用尺规完成下列作图(只保留作图痕迹,不要求写出作法).
1. 如图,在直线l上求作一点P,使PA= PB.
随堂演练
2. 如图,作出△ABC的BC边上的高.
2.4 第2课时 线段垂直平分线、垂线的作法
知识回顾
二、逆定理(判定定理):
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线
一、性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
如图,已知线段AB,作线段AB 的垂直平分线.
根据“到线段两端距离相等的点在线段的垂直平分线上”,要作线段AB的垂直平分线,关键是找出到线段AB两端距离相等的两点.
获取新知
作法
①分别以点A,B 为圆心, 以大于 AB 的长为半径画弧, 两弧相交于点C 和点D;
②过点C,D作直线CD,则直线CD就是线段AB的垂直平分线.
因为线段AB的垂直平分线CD与线段AB的交点就是线段AB的中点,所以可以用这种方法作出线段的中点.
如何过一点P作已知直线l的垂线呢?
由于两点确定一条直线, 因此我们可以通过在已知直线上作线段的垂直平分线来找出垂线上的另一点,从而确定已知直线的垂线.
(1)当点P在直线l上.
(2)当点P在直线l外.
点P与已知直线l的位置关系有两种:
①在直线l 上点P 的两旁分别截取线段PA, PB,使PA= PB;
(1)当点P在直线l上.
②分别以A,B 为圆心 以大于 AB 的长为半径画弧, 两弧相交于点C;
③过点C, P作直线CP, 则直线CP为所求作的直线.
(2) 当点P在直线l外.
①以点P 为圆心, 以大于点P 到直线l的距离的线段长为半径画弧, 交直线l于点A,B;
②分别以A,B 为圆心 以大于 AB 的长为半径画弧, 两弧相交于点C;
③过点C,P作直线CP,则直线CP为所求作的直线.
例题讲解
线段的垂直平分线
一、性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
课堂小结
二、逆定理(判定定理):
到线段两个端点距离相等的点,在这条线段的垂直平分线上。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
课堂小结
用尺规完成下列作图(只保留作图痕迹,不要求写出作法).
1. 如图,在直线l上求作一点P,使PA= PB.
随堂演练
2. 如图,作出△ABC的BC边上的高.
同课章节目录
