2021-2022学年湘教版数学八年级上册 1.3.2 零次幂和负整数指数幂---同步课件 (共18张ppt)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级上册 1.3.2 零次幂和负整数指数幂---同步课件 (共18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 525.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览




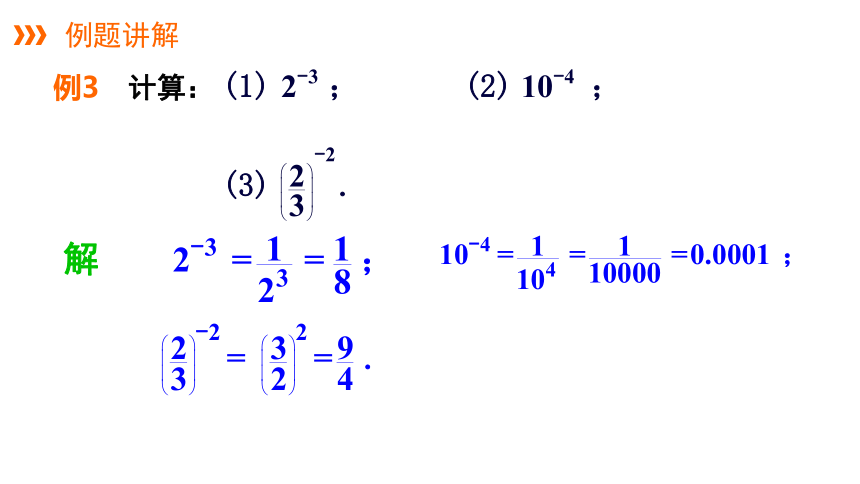

文档简介
(共18张PPT)
第1章
分式
1.3.2 零次幂和负整数指数幂
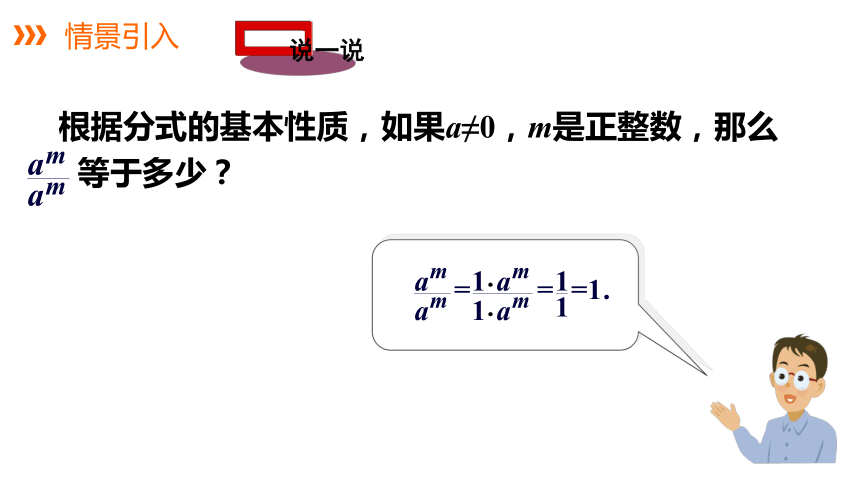
情景引入
说一说
根据分式的基本性质,如果a≠0,m是正整数,那么
等于多少?
获取新知
这启发我们规定
例如,
20=1,100=1,
,x0=1(x≠0)
.
a0=1(a≠0).
如果把公式
(a≠0,m,n都是正整数,且m>n)推广到
m=n
的情形,那么就会有
即
任何不等于零的数的零次幂都等于1.
情景引入
设a≠0,n是正整数,试问:a-n等于什么?
动脑筋
获取新知
因为a0-n
=
a-n,这启发我们规定
由于
因此
特别地,
(a≠0,n是正整数).
(a≠0,n是正整数).
任何一个不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数
例题讲解
例3
计算:
例题讲解
例4
把下列各式写成分式的形式:
(1)x
-2;
(2)2xy
-3.
例题讲解
例5
用小数表示3.6×10-3.
解
3.6×10-3
=
3.6×0.001
=
0.0036.
=
3.6×
获取新知
在七年级上册中,我们学过用科学记数法把一些绝对值较大的数表示成a×10n的形式,其中n是正整数,1≤|a|<
10.
类似地,利用10的负整数次幂,我们可以用科学记数法表示一些绝对值较小的数;
即将它们表示成
a×10-n
的形式,其中n是正整数,1≤|a|<
10.
获取新知
这里用科学记数法表示时,关键是掌握公式:
0.00
…
01
=
10-n.
n个0
n为从左至右数,在第一个非零整数位前零的个数。
用科学计数法表示数的符号跟原数的符号一致,即原数是负数,用科学计数法时不能漏掉负号。
例题讲解
例6
2010年,国外科学家成功制造出世界上最小的晶体管,它的长度只有0.00000004m,请用科学记数法表示它的长度,并在计算器上把它表示出来.
解
0.00000004
=
4×0.00000001
=
4
×
10-8.
例题讲解
在计算器上依次按键输入0.00000004,
最后按“=”键,屏幕显示如下,表示4×10-8.
随堂演练
练习
1.
计算:
0.50,(-1)0,10-5,
,
.
解
0.50
=
1,
(-1)0
=
1,
10-5
=
0.00001,
随堂演练
2.
把下列各式写成分式的形式:
(1)x-3;
(2)-5x-2y3.
随堂演练
3.
用小数表示5.6×10-4.
解
5.6
×
10-4
=0.00056
.
解
0.00000005
=
5
×
10-8.
4.
2011年3月,英国和新加坡研究人员制造出观测极限为0.00000005m的光学显微镜,这是迄今为止观测能力最强的光学显微镜,请用科学记数法表示这个数.
课堂小结
a-n应用时的“两变”“三注意”:
(1)“两变”:
①底数由a变成了1/a;
②指数由-n变成了n.
课堂小结
(2)“三注意”:
①注意条件a≠0;
②负整数指数幂的负号是指数的性质符号,不是幂值的符号,不能移到幂的结果前;
③负整数指数幂一定要先化为正整数指数幂.
课堂小结
第1章
分式
1.3.2 零次幂和负整数指数幂
情景引入
说一说
根据分式的基本性质,如果a≠0,m是正整数,那么
等于多少?
获取新知
这启发我们规定
例如,
20=1,100=1,
,x0=1(x≠0)
.
a0=1(a≠0).
如果把公式
(a≠0,m,n都是正整数,且m>n)推广到
m=n
的情形,那么就会有
即
任何不等于零的数的零次幂都等于1.
情景引入
设a≠0,n是正整数,试问:a-n等于什么?
动脑筋
获取新知
因为a0-n
=
a-n,这启发我们规定
由于
因此
特别地,
(a≠0,n是正整数).
(a≠0,n是正整数).
任何一个不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数
例题讲解
例3
计算:
例题讲解
例4
把下列各式写成分式的形式:
(1)x
-2;
(2)2xy
-3.
例题讲解
例5
用小数表示3.6×10-3.
解
3.6×10-3
=
3.6×0.001
=
0.0036.
=
3.6×
获取新知
在七年级上册中,我们学过用科学记数法把一些绝对值较大的数表示成a×10n的形式,其中n是正整数,1≤|a|<
10.
类似地,利用10的负整数次幂,我们可以用科学记数法表示一些绝对值较小的数;
即将它们表示成
a×10-n
的形式,其中n是正整数,1≤|a|<
10.
获取新知
这里用科学记数法表示时,关键是掌握公式:
0.00
…
01
=
10-n.
n个0
n为从左至右数,在第一个非零整数位前零的个数。
用科学计数法表示数的符号跟原数的符号一致,即原数是负数,用科学计数法时不能漏掉负号。
例题讲解
例6
2010年,国外科学家成功制造出世界上最小的晶体管,它的长度只有0.00000004m,请用科学记数法表示它的长度,并在计算器上把它表示出来.
解
0.00000004
=
4×0.00000001
=
4
×
10-8.
例题讲解
在计算器上依次按键输入0.00000004,
最后按“=”键,屏幕显示如下,表示4×10-8.
随堂演练
练习
1.
计算:
0.50,(-1)0,10-5,
,
.
解
0.50
=
1,
(-1)0
=
1,
10-5
=
0.00001,
随堂演练
2.
把下列各式写成分式的形式:
(1)x-3;
(2)-5x-2y3.
随堂演练
3.
用小数表示5.6×10-4.
解
5.6
×
10-4
=0.00056
.
解
0.00000005
=
5
×
10-8.
4.
2011年3月,英国和新加坡研究人员制造出观测极限为0.00000005m的光学显微镜,这是迄今为止观测能力最强的光学显微镜,请用科学记数法表示这个数.
课堂小结
a-n应用时的“两变”“三注意”:
(1)“两变”:
①底数由a变成了1/a;
②指数由-n变成了n.
课堂小结
(2)“三注意”:
①注意条件a≠0;
②负整数指数幂的负号是指数的性质符号,不是幂值的符号,不能移到幂的结果前;
③负整数指数幂一定要先化为正整数指数幂.
课堂小结
同课章节目录
