三年级下册数学教案-7.5 整理与提高 数学广场(谁围出的面积更大) 沪教版
文档属性
| 名称 | 三年级下册数学教案-7.5 整理与提高 数学广场(谁围出的面积更大) 沪教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 62.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览

文档简介
谁围出的面积大
教学目标:
通过复习正方形填表,找到规律:周长相等的正方形,面积一定相等。
通过复习长方形填表,找到规律:周长相等的长方形,面积不一定相等。长与宽的和等于周长的一半。
在围图形的过程中,学习如何有序地列举出长和宽。
在数据中发现:周长相等时,围成的正方形面积最大;周长相等但不能围成正方形时,长与宽最接近,面积最大。
教学重点:
让学生感悟:周长相等的长方形,面积不一定相等;周长相等的正方形,面积一定相等
在数据中发现规律:周长相等时,围成的正方形面积最大;周长相等但不能围成正方形时,长与宽最接近,面积最大。
教学难点:
1、周长相等的长方形如何有序列举出长和宽
2、在数据中发现规律:周长相等时,围成的正方形面积最大;周长相等但不能围成正方形时,长与宽最接近,面积最大。
教学过程:
复习
长方形、正方形的周长、面积公式
新知探索
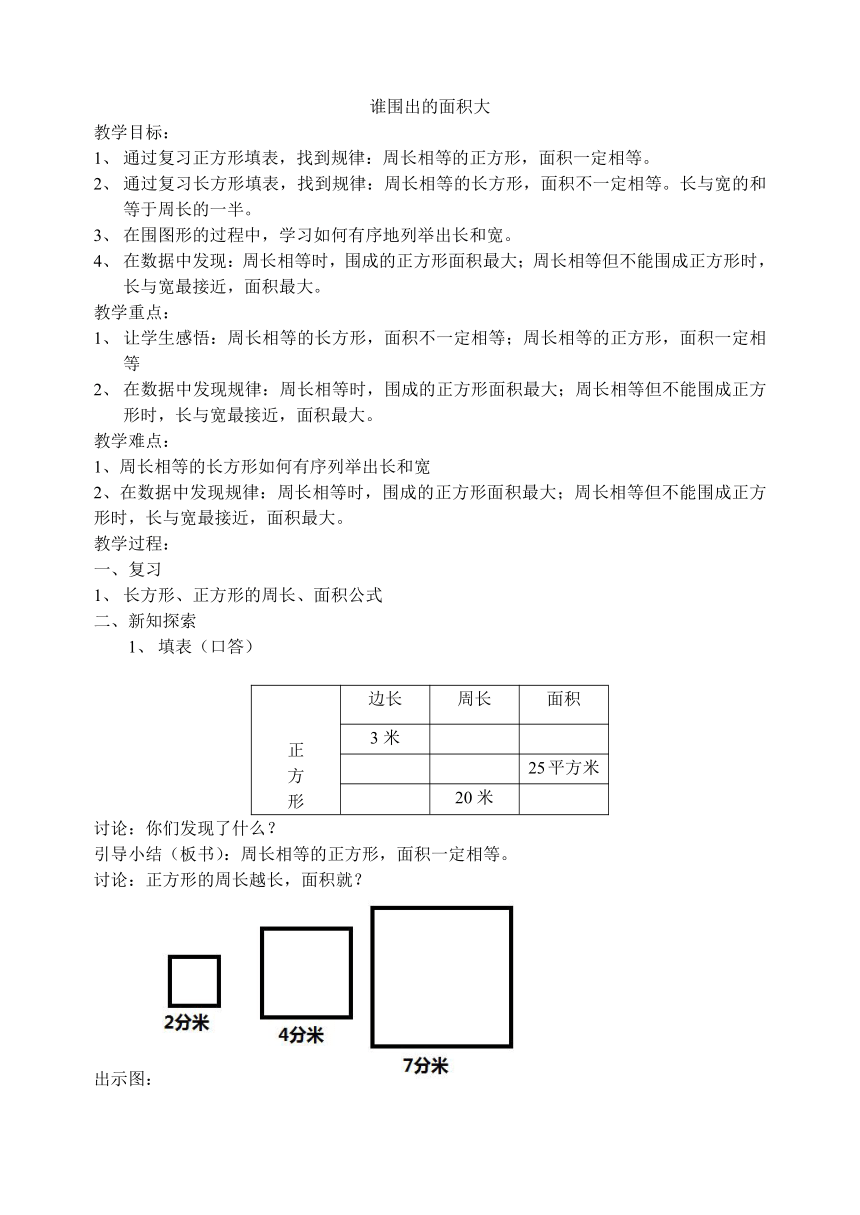
填表(口答)
正
方
形 边长 周长 面积
3米
25平方米
20米
讨论:你们发现了什么?
引导小结(板书):周长相等的正方形,面积一定相等。
讨论:正方形的周长越长,面积就?
出示图:
口答验证,小结:正方形的周长越长,面积就越大;正方形的周长越短,面积就越小。
2、填表(口答)
长
方
形 长 宽 周长 面积
5米 1米
4米 2米
3米 3米
讨论,你们发现了什么?
引导小结:周长相等的长方形,面积不相等。
讨论:还有什么发现?(提醒:观察长+宽的和与周长之间的关系)
引导小结:长+宽的和是周长的一半。
讨论:再仔细观察一下长和宽,你们认为这组数据怎么样?
渗透:有序(板书)
3、周长相等的长方形,面积不一样。那什么时候面积最大呢?(揭示课题:谁围成的面积最大))
学生操作:用20根小棒围成长方形。
学生先试着猜想,能围成几种图形?之后操作:你能围成几种就记录几种
周长 长+宽 长 宽 面积
20
10 9 1 9
8 2 16
7 3 21
6 4 24
5 5 25
学生边汇报,师有序地将数据填入表格。
引导小结(板书):周长相等的长方形的正方形面积最大。长与宽越接近,面积就最大。
师:那如果不借助小棒,你能通过计算算出围成的正方形面积吗?
板书:边长:20÷4=5
面积:5×5=25
学生动手算一算:当周长是16cm和周长是40cm时,围成的最大图形的面积。
如果周长是22,能围成正方形吗?不操作列举出长和宽,算算什么时候面积最大?
周长 长+宽 长 宽 面积
22
11 10 1 10
9 2 18
8 3 24
7 4 28
6 5 30
观察:什么时候面积最大?
引导小结(板书):周长相等的长方形,长与宽相差越小(即越接近),围成的面积越大。
钉子板上操作加以理解。
学生动手写一写,周长是14时,长和宽分别是几?面积最大是几?
练习
学生练习纸:周长是32厘米时,围成的什么图形面积最大?该图形的面积是多少?
周长是18时,围成的长方形长和宽可以是几(一一列举出来),面积最大是几?(投影核对)
判断:(1)周长是28的正方形面积比周长是32的正方形面积一定小吗?
(学生可以算一算)
(2)长方形周长越长,面积也越大吗?
利用课上的两张表格(周长是20,周长是22),让学生在两张表格的对比中得出结论。
(教师出示
即使周长很长,但是面积却很小)
我们的易错题:24×5 25×4,答案一样吗?谁的积大?
结论:两个因数的和相等时,差小,积就大。
想一想:下列算式中,和都是30,哪个算式的积最大?
A、12X18 B、19X11 C、15X15 D、16X14
板书:
谁围成的面积最大
周长相等的正方形,面积一定相等。
周长相等的长方形,面积不一定相等。
周长相等的长方形,围成的正方形面积最大。
长与宽的差最小,面积最大。
教学目标:
通过复习正方形填表,找到规律:周长相等的正方形,面积一定相等。
通过复习长方形填表,找到规律:周长相等的长方形,面积不一定相等。长与宽的和等于周长的一半。
在围图形的过程中,学习如何有序地列举出长和宽。
在数据中发现:周长相等时,围成的正方形面积最大;周长相等但不能围成正方形时,长与宽最接近,面积最大。
教学重点:
让学生感悟:周长相等的长方形,面积不一定相等;周长相等的正方形,面积一定相等
在数据中发现规律:周长相等时,围成的正方形面积最大;周长相等但不能围成正方形时,长与宽最接近,面积最大。
教学难点:
1、周长相等的长方形如何有序列举出长和宽
2、在数据中发现规律:周长相等时,围成的正方形面积最大;周长相等但不能围成正方形时,长与宽最接近,面积最大。
教学过程:
复习
长方形、正方形的周长、面积公式
新知探索
填表(口答)
正
方
形 边长 周长 面积
3米
25平方米
20米
讨论:你们发现了什么?
引导小结(板书):周长相等的正方形,面积一定相等。
讨论:正方形的周长越长,面积就?
出示图:
口答验证,小结:正方形的周长越长,面积就越大;正方形的周长越短,面积就越小。
2、填表(口答)
长
方
形 长 宽 周长 面积
5米 1米
4米 2米
3米 3米
讨论,你们发现了什么?
引导小结:周长相等的长方形,面积不相等。
讨论:还有什么发现?(提醒:观察长+宽的和与周长之间的关系)
引导小结:长+宽的和是周长的一半。
讨论:再仔细观察一下长和宽,你们认为这组数据怎么样?
渗透:有序(板书)
3、周长相等的长方形,面积不一样。那什么时候面积最大呢?(揭示课题:谁围成的面积最大))
学生操作:用20根小棒围成长方形。
学生先试着猜想,能围成几种图形?之后操作:你能围成几种就记录几种
周长 长+宽 长 宽 面积
20
10 9 1 9
8 2 16
7 3 21
6 4 24
5 5 25
学生边汇报,师有序地将数据填入表格。
引导小结(板书):周长相等的长方形的正方形面积最大。长与宽越接近,面积就最大。
师:那如果不借助小棒,你能通过计算算出围成的正方形面积吗?
板书:边长:20÷4=5
面积:5×5=25
学生动手算一算:当周长是16cm和周长是40cm时,围成的最大图形的面积。
如果周长是22,能围成正方形吗?不操作列举出长和宽,算算什么时候面积最大?
周长 长+宽 长 宽 面积
22
11 10 1 10
9 2 18
8 3 24
7 4 28
6 5 30
观察:什么时候面积最大?
引导小结(板书):周长相等的长方形,长与宽相差越小(即越接近),围成的面积越大。
钉子板上操作加以理解。
学生动手写一写,周长是14时,长和宽分别是几?面积最大是几?
练习
学生练习纸:周长是32厘米时,围成的什么图形面积最大?该图形的面积是多少?
周长是18时,围成的长方形长和宽可以是几(一一列举出来),面积最大是几?(投影核对)
判断:(1)周长是28的正方形面积比周长是32的正方形面积一定小吗?
(学生可以算一算)
(2)长方形周长越长,面积也越大吗?
利用课上的两张表格(周长是20,周长是22),让学生在两张表格的对比中得出结论。
(教师出示
即使周长很长,但是面积却很小)
我们的易错题:24×5 25×4,答案一样吗?谁的积大?
结论:两个因数的和相等时,差小,积就大。
想一想:下列算式中,和都是30,哪个算式的积最大?
A、12X18 B、19X11 C、15X15 D、16X14
板书:
谁围成的面积最大
周长相等的正方形,面积一定相等。
周长相等的长方形,面积不一定相等。
周长相等的长方形,围成的正方形面积最大。
长与宽的差最小,面积最大。
