2021年暑假九年级数学苏科版上册《2.3确定圆的条件》自主学习能力提升训练(word版附答案)
文档属性
| 名称 | 2021年暑假九年级数学苏科版上册《2.3确定圆的条件》自主学习能力提升训练(word版附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 298.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览




文档简介
2021年苏科版九年级数学上册《2.3确定圆的条件》暑假自主学习能力提升训练(附答案)
一.选择题
1.经过不在同一直线上的三个点可以作圆的个数是( )
A.1 B.2 C.3 D.无数
2.下列说法正确的是( )
A.长度相等的两条弧是等弧 B.三点确定一个圆
C.同一条弦所对的两条弧一定是等弧 D.半圆是弧
3.若⊙O的半径为r,点P到圆心O的距离d不大于r,则点P( )
A.在⊙O内 B.在⊙O外 C.不在⊙O内 D.不在⊙O外
4.下列语句中,正确的个数是( )
①相等的圆心角所对的弦相等;②三点确定一个圆;③平分弦的直径垂直于弦;④圆的每一条直径所在的直线都是它的对称轴.
A.1个 B.2个 C.3个 D.4个
5.在△ABC中,∠C=90°,以点B为圆心,以BC长为半径作圆,点A与该圆的位置关系为( )
A.点A在圆外 B.点A在圆内 C.点A在圆上 D.无法确定
6.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.均不可能
7.如图,⊙O是△ABC的外接圆,已知∠ACB=50°,则∠ABO的大小为( )
A.30° B.40° C.45° D.50°
二.填空题
8.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是 .
9.当点A(1,2),B(3,﹣3),C(m,n)三点可以确定一个圆时,m,n需要满足的条件 .
10.如图,AD是△ABC的外接圆⊙O的直径,若∠BCA=50°,则∠ADB= °.
11.如图,△ABC内接于⊙O,∠BAC=30°,BC=2,则⊙O的直径等于 .
12.△ABC内接于圆O,且AB=AC,圆O的半径等于6cm,O点到BC距离等于2cm,则AB长为 cm.
13.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .
14.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为 .
15.在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为(,0)、(3,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
16.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
17.如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为2,则CD的长为 .
三.解答题
18.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
19.如图,在直角坐标系中,已知点A(0,4),B(﹣4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求DO+DA的最小值.
20.如图,AB是圆O的直径,点C、D为圆O上的点,满足:=,AD交OC于点E.已知OE=3,EC=2.
(1)求弦AD的长;
(2)请过点C作AB的平行线交弦AD于点F,求线段EF的长.
21.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
22.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
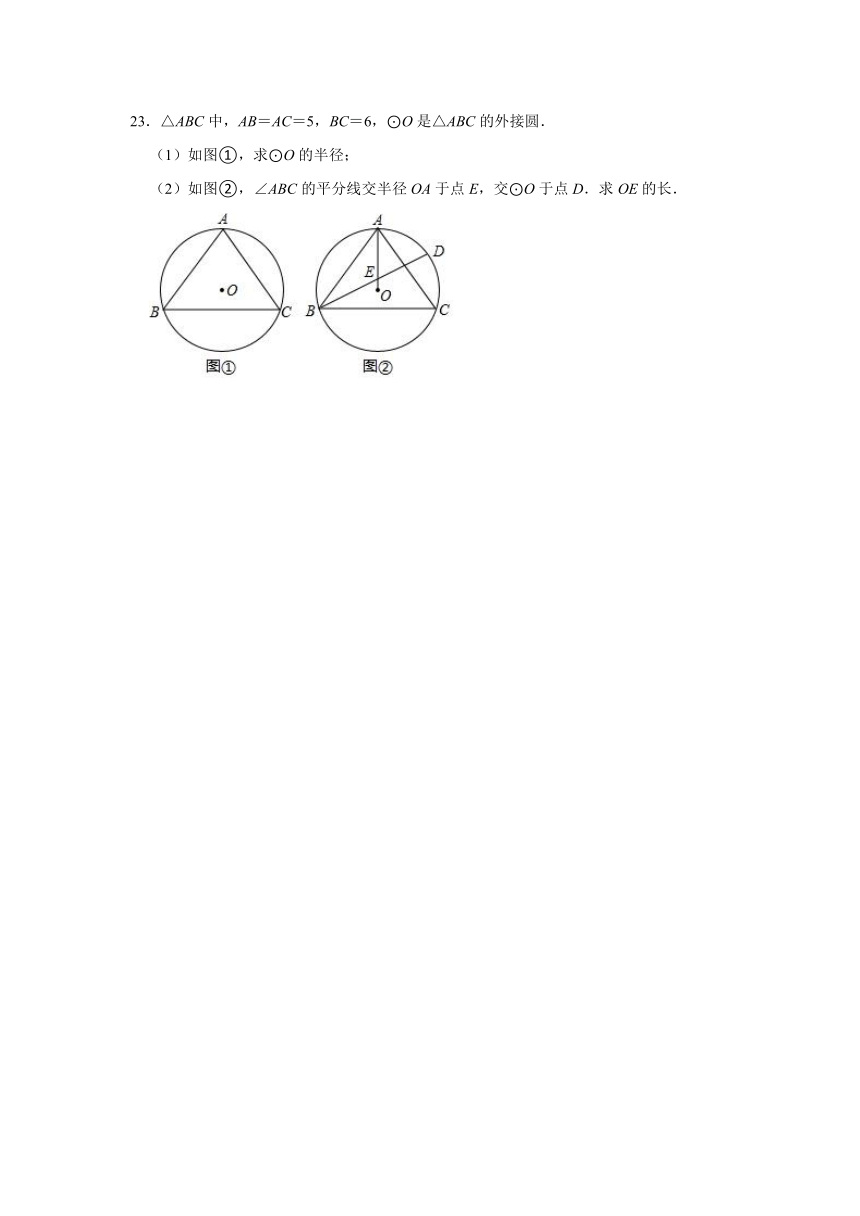
23.△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
参考答案
一.选择题
1.解:经过不在同一直线上的三点确定一个圆.
故选:A.
2.解:A、长度相等的两条弧不一定是等弧,所以A选项错误;
B、不共线的三点确定一个圆,所以B选项错误;
C、同一条弦所对的两条弧不一定是等弧,所以C选项错误;
D、半圆是弧,所以D选项正确.
故选:D.
3.解:已知点P到圆心O的距离d不大于r,当大于r时点P在圆外,因而则点P不在⊙O外.
故选:D.
4.解:同圆或等圆中,相等的圆心角所对的弦相等,故①错误;
不在同一直线上的三点确定一个圆,故②错误;
平分弦(不是直径)的直径垂直于弦,故③错误;
圆的每一条直径所在的直线都是它的对称轴,故④正确;
故选:A.
5.解:∵在△ABC中,∠C=90°,
∴AB>BC,
∴点A在圆外.
故选:A.
6.解:第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
7.解:∵∠ACB=50°,
∴∠AOB=100°,
∵AO=BO,
∴∠ABO=(180°﹣100°)÷2=40°,
故选:B.
二.填空题
8.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=8,BC=6,
∴AC=10,
∵AN=NC,
∴BN=AC=5,
∵AN=NC,DM=MC,
∴MN==2,
∴BM≤BN+NM,
∴BM≤5+2=7,
即BM的最大值是7.
故答案为7.
9.解:设直线AB的解析式为y=kx+b,
∵A(1,2),B(3,﹣3),
∴
解得:k=﹣,b=,
∴直线AB的解析式为y=﹣+,
∵点A(1,2),B(3,﹣3),C(m,n)三点可以确定一个圆时,
∴点C不在直线AB上,
∴5m+2n≠9,
故答案为:5m+2n≠9.
10.解:∵AD是△ABC的外接圆⊙O的直径,
∴点A,B,C,D在⊙O上,
∵∠BCA=50°,
∴∠ADB=∠BCA=50°,
故答案为:50.
11.解:作直径BD,连接CD,
由圆周角定理得,∠D=∠BAC=30°,∠BCD=90°,
∴BD=2BC=4,
故答案为:4.
12.解:①当圆心在三角形内部时(如图1),
连接AO并延长交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2﹣AD2=BO2﹣OD2=BD2,
AB2﹣(6+2)2=62﹣22,解得AB=4;
②当圆心在三角形外部时(如图2),
连接AO交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2﹣AD2=BO2﹣OD2=BD2,
AB2﹣(6﹣2)2=62﹣22,解得AB=4.
∴AB=4或4cm.
故本题答案为:4或4.
13.解:如图,
∵AE⊥BE,
∴点E在以AB为直径的半⊙O上,
连接CO交⊙O于点E′,
∴当点E位于点E′位置时,线段CE取得最小值,
∵AB=4,
∴OA=OB=OE′=2,
∵BC=6,
∴OC===2,
则CE′=OC﹣OE′=2﹣2,
故答案为:2﹣2.
14.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
15.解:作圆,使∠ADB=60°,设圆心为P,连接PA、PB、PC,PE⊥AB于E,如图所示:
∵A(,0)、B(3,0),
∴E(2,0)
又∠ADB=60°,
∴∠APB=120°,
∴PE=1,PA=2PE=2,
∴P(2,1),
∵C(0,5),
∴PC==2,
又∵PD=PA=2,
∴只有点D在线段PC上时,CD最短(点D在别的位置时构成△CDP)
∴CD最小值为:2﹣2.
故答案为:2﹣2.
16.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
17.解:连接CO,OB,
则∠O=2∠A=60°,
∵OC=OB,
∴△BOC是等边三角形,
∵⊙O的半径为2,
∴BC=2,
∵CD⊥AB,∠CBA=45°,
∴CD=BC=,
故答案为:.
三.解答题
18.解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF?BD=AB?AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
19.解:如图,设△ABC的外接圆的圆心为E连接EO并且延长交AC的延长线于F,连接DF.则E(﹣1,1).
∵A(0,4),B(﹣4,0),C(2,0),E(﹣1,1)
∴直线OE的解析式为y=﹣x,直线AC的解析式为y=﹣2x+4,
由解得,
∴F(4,﹣4),
∴DE=,EO=,EF=5,
∴DF=DO,
∴DO+DA=DF+DA,由两边之和大于第三边得,DF+DA≥AF,
∴当点D和点C重合时,DF+DA最小,即DO+DA最小,
∴DO+DA最小值=AF==4.
20.解:(1)由=,得CO⊥AD,AE=DE,
在△AOE中,∠AEO=90°,OE=3,OA=OC=OE+CE=5,
得AE=,
所以AD=AE+DE=8;
(2)由CF∥AB,
则.
21.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
22.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
答:圆的半径为13cm.
23.解:(1)过A点作AH⊥BC于H,如图①,
∵AB=AC,
∴BH=CH=BC=3,
即AH垂直平分BC,
∴点O在AH上,
在Rt△ABH中,AH==4,
连接OB,设⊙O的半径为r,则OB=r,OH=AH﹣OA=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,解得r=,
即⊙O的半径为;
(2)作EF⊥AB于F,如图,
∵BD平分∠ABC,
∴EH=EF,
∵S△ABE=BH?AE=AB?EF,
∴EH=AH=×4=,
由(1)得OH=AH﹣OA=4﹣=,
∴OE=﹣=.
一.选择题
1.经过不在同一直线上的三个点可以作圆的个数是( )
A.1 B.2 C.3 D.无数
2.下列说法正确的是( )
A.长度相等的两条弧是等弧 B.三点确定一个圆
C.同一条弦所对的两条弧一定是等弧 D.半圆是弧
3.若⊙O的半径为r,点P到圆心O的距离d不大于r,则点P( )
A.在⊙O内 B.在⊙O外 C.不在⊙O内 D.不在⊙O外
4.下列语句中,正确的个数是( )
①相等的圆心角所对的弦相等;②三点确定一个圆;③平分弦的直径垂直于弦;④圆的每一条直径所在的直线都是它的对称轴.
A.1个 B.2个 C.3个 D.4个
5.在△ABC中,∠C=90°,以点B为圆心,以BC长为半径作圆,点A与该圆的位置关系为( )
A.点A在圆外 B.点A在圆内 C.点A在圆上 D.无法确定
6.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.均不可能
7.如图,⊙O是△ABC的外接圆,已知∠ACB=50°,则∠ABO的大小为( )
A.30° B.40° C.45° D.50°
二.填空题
8.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是 .
9.当点A(1,2),B(3,﹣3),C(m,n)三点可以确定一个圆时,m,n需要满足的条件 .
10.如图,AD是△ABC的外接圆⊙O的直径,若∠BCA=50°,则∠ADB= °.
11.如图,△ABC内接于⊙O,∠BAC=30°,BC=2,则⊙O的直径等于 .
12.△ABC内接于圆O,且AB=AC,圆O的半径等于6cm,O点到BC距离等于2cm,则AB长为 cm.
13.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .
14.在平面直角坐标系中有A,B,C三点,A(1,3),B(3,3),C(5,1).现在要画一个圆同时经过这三点,则圆心坐标为 .
15.在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为(,0)、(3,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
16.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
17.如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为2,则CD的长为 .
三.解答题
18.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
19.如图,在直角坐标系中,已知点A(0,4),B(﹣4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求DO+DA的最小值.
20.如图,AB是圆O的直径,点C、D为圆O上的点,满足:=,AD交OC于点E.已知OE=3,EC=2.
(1)求弦AD的长;
(2)请过点C作AB的平行线交弦AD于点F,求线段EF的长.
21.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
22.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
23.△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
参考答案
一.选择题
1.解:经过不在同一直线上的三点确定一个圆.
故选:A.
2.解:A、长度相等的两条弧不一定是等弧,所以A选项错误;
B、不共线的三点确定一个圆,所以B选项错误;
C、同一条弦所对的两条弧不一定是等弧,所以C选项错误;
D、半圆是弧,所以D选项正确.
故选:D.
3.解:已知点P到圆心O的距离d不大于r,当大于r时点P在圆外,因而则点P不在⊙O外.
故选:D.
4.解:同圆或等圆中,相等的圆心角所对的弦相等,故①错误;
不在同一直线上的三点确定一个圆,故②错误;
平分弦(不是直径)的直径垂直于弦,故③错误;
圆的每一条直径所在的直线都是它的对称轴,故④正确;
故选:A.
5.解:∵在△ABC中,∠C=90°,
∴AB>BC,
∴点A在圆外.
故选:A.
6.解:第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
7.解:∵∠ACB=50°,
∴∠AOB=100°,
∵AO=BO,
∴∠ABO=(180°﹣100°)÷2=40°,
故选:B.
二.填空题
8.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=8,BC=6,
∴AC=10,
∵AN=NC,
∴BN=AC=5,
∵AN=NC,DM=MC,
∴MN==2,
∴BM≤BN+NM,
∴BM≤5+2=7,
即BM的最大值是7.
故答案为7.
9.解:设直线AB的解析式为y=kx+b,
∵A(1,2),B(3,﹣3),
∴
解得:k=﹣,b=,
∴直线AB的解析式为y=﹣+,
∵点A(1,2),B(3,﹣3),C(m,n)三点可以确定一个圆时,
∴点C不在直线AB上,
∴5m+2n≠9,
故答案为:5m+2n≠9.
10.解:∵AD是△ABC的外接圆⊙O的直径,
∴点A,B,C,D在⊙O上,
∵∠BCA=50°,
∴∠ADB=∠BCA=50°,
故答案为:50.
11.解:作直径BD,连接CD,
由圆周角定理得,∠D=∠BAC=30°,∠BCD=90°,
∴BD=2BC=4,
故答案为:4.
12.解:①当圆心在三角形内部时(如图1),
连接AO并延长交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2﹣AD2=BO2﹣OD2=BD2,
AB2﹣(6+2)2=62﹣22,解得AB=4;
②当圆心在三角形外部时(如图2),
连接AO交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2﹣AD2=BO2﹣OD2=BD2,
AB2﹣(6﹣2)2=62﹣22,解得AB=4.
∴AB=4或4cm.
故本题答案为:4或4.
13.解:如图,
∵AE⊥BE,
∴点E在以AB为直径的半⊙O上,
连接CO交⊙O于点E′,
∴当点E位于点E′位置时,线段CE取得最小值,
∵AB=4,
∴OA=OB=OE′=2,
∵BC=6,
∴OC===2,
则CE′=OC﹣OE′=2﹣2,
故答案为:2﹣2.
14.解:∵A(1,3),B(3,3),C(5,1)不在同一直线上
∴经过点A,B,C可以确定一个圆
∴该圆圆心必在线段AB的垂直平分线上
∴设圆心坐标为M(2,m)
则点M在线段BC的垂直平分线上
∴MB=MC
由勾股定理得:=
∴1+m2﹣6m+9=9+m2﹣2m+1
∴m=0
∴圆心坐标为M(2,0)
故答案为:(2,0).
15.解:作圆,使∠ADB=60°,设圆心为P,连接PA、PB、PC,PE⊥AB于E,如图所示:
∵A(,0)、B(3,0),
∴E(2,0)
又∠ADB=60°,
∴∠APB=120°,
∴PE=1,PA=2PE=2,
∴P(2,1),
∵C(0,5),
∴PC==2,
又∵PD=PA=2,
∴只有点D在线段PC上时,CD最短(点D在别的位置时构成△CDP)
∴CD最小值为:2﹣2.
故答案为:2﹣2.
16.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
17.解:连接CO,OB,
则∠O=2∠A=60°,
∵OC=OB,
∴△BOC是等边三角形,
∵⊙O的半径为2,
∴BC=2,
∵CD⊥AB,∠CBA=45°,
∴CD=BC=,
故答案为:.
三.解答题
18.解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF?BD=AB?AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
19.解:如图,设△ABC的外接圆的圆心为E连接EO并且延长交AC的延长线于F,连接DF.则E(﹣1,1).
∵A(0,4),B(﹣4,0),C(2,0),E(﹣1,1)
∴直线OE的解析式为y=﹣x,直线AC的解析式为y=﹣2x+4,
由解得,
∴F(4,﹣4),
∴DE=,EO=,EF=5,
∴DF=DO,
∴DO+DA=DF+DA,由两边之和大于第三边得,DF+DA≥AF,
∴当点D和点C重合时,DF+DA最小,即DO+DA最小,
∴DO+DA最小值=AF==4.
20.解:(1)由=,得CO⊥AD,AE=DE,
在△AOE中,∠AEO=90°,OE=3,OA=OC=OE+CE=5,
得AE=,
所以AD=AE+DE=8;
(2)由CF∥AB,
则.
21.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
22.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
答:圆的半径为13cm.
23.解:(1)过A点作AH⊥BC于H,如图①,
∵AB=AC,
∴BH=CH=BC=3,
即AH垂直平分BC,
∴点O在AH上,
在Rt△ABH中,AH==4,
连接OB,设⊙O的半径为r,则OB=r,OH=AH﹣OA=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,解得r=,
即⊙O的半径为;
(2)作EF⊥AB于F,如图,
∵BD平分∠ABC,
∴EH=EF,
∵S△ABE=BH?AE=AB?EF,
∴EH=AH=×4=,
由(1)得OH=AH﹣OA=4﹣=,
∴OE=﹣=.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
