2.5 等腰三角形的轴对称性同步练习 2021-2022学年苏科版八年级数学上册(word版含答案)
文档属性
| 名称 | 2.5 等腰三角形的轴对称性同步练习 2021-2022学年苏科版八年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 183.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 06:20:57 | ||
图片预览




文档简介
2.5 等腰三角形的轴对称性
一、选择题
1. 在△ABC中,∠B=50°,∠A=80°,若AB=6,则AC的长为 ( )
A.6 B.8
C.5 D.13
2.如图2,直线l分别与直线AB,CD相交于点E,F,EG平分 ∠BEF交直线CD于点G,若∠1=∠BEF,EF=3,则FG的长为 ( )
图2
A.4 B.3
C.5 D.1.5
3.如图3,在△ABC中,AB=AC,点D在CA的延长线上,DE⊥BC于点E,∠BAC=100°,则∠D的度数为 ( )
图3
A.40° B.50°
C.60° D.80°
4.如图4,AC,BD相交于点O,∠A=∠D,如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是 ( )
图4
A.OA=OD B.AB=CD
C.∠ABO=∠DCO D.∠ABC=∠DCB
5.如图5,在等边三角形ABC中,D为AC边的中点,E为BC边的延长线上一点,CE=CD,DM⊥BC于点M.下列结论错误的是 ( )
图5
A.BM=3CM B.BM=EM
C.CM=12CE D.DM=2CM
二、填空题
6.已知一个等腰三角形的一个内角为40°,则它的顶角等于 .?
7.房梁的一部分如图6所示,其中BC⊥AC,∠A=30°,AB=8 m, D是AB的中点,且DE⊥AC,垂足为E,则DE的长为 m.?
图6
8.如图7,在△ABC中,BE平分∠ABC,CE平分∠ACB,BE和CE交于点E,过点E作MN∥BC交AB于点M,交AC于点N.若MN=8,则BM+CN的长为 .?
图7
9.如图8,在△ABC中,AB=AC,D为BC上一点,且AD=DE,∠BAD=20°,∠EDC=10°,则∠ADE= °.?
图8
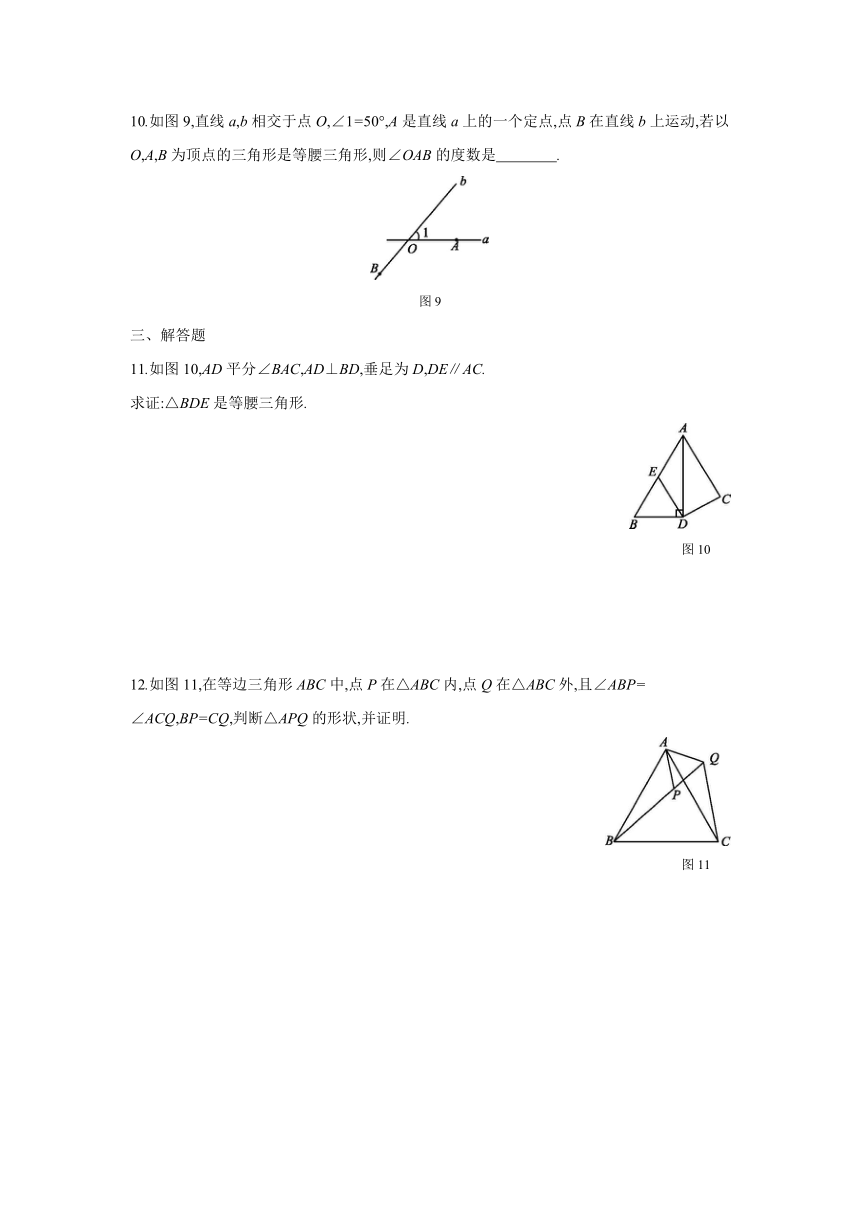
10.如图9,直线a,b相交于点O,∠1=50°,A是直线a上的一个定点,点B在直线b上运动,若以O,A,B为顶点的三角形是等腰三角形,则∠OAB的度数是 .?
图9
三、解答题
11.如图10,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.
求证:△BDE是等腰三角形.
图10
12.如图11,在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=
∠ACQ,BP=CQ,判断△APQ的形状,并证明.
图11
13.如图12,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,连接MC,NC,DM与EN相交于点F.
(1)若AB=21 cm,则△CMN的周长= cm;?
(2)若∠MFN=80°,求∠MCN的度数.
图12
14.如图13,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过点D作DE∥AC,交AB于点E.若AB=5,求线段DE的长.
图13
15.[2020·阜新太平区期末] 已知:如图14,C为线段AB上一点,△ACM,△CBN都是等边三角形,连接AN交MC于点E,连接BM交CN于点F,连接EF.
(1)求证:AN=BM;
(2)求证:△CEF为等边三角形.
图14
16.在△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图15,若E,F分别是AB,AC上的点,且BE=AF.求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,则△DEF是否仍为等腰直角三角形?证明你的结论.
图15
答案
1.A [解析] ∵在△ABC中,∠B=50°,∠A=80°,∴∠C=180°-∠A-∠B=180°-80°-50°=50°,
∴∠C=∠B,∴AC=AB=6.故选A.
2.B [解析] ∵EG平分∠BEF,∴∠GEB=∠GEF.∵∠1=∠BEF,∴CD∥AB,
∴∠EGF=∠GEB,∴∠GEF=∠EGF,则FG=EF=3.故选B.
3.B [解析] ∵AB=AC,∠BAC=100°,∴∠C=∠B=40°.∵DE⊥BC于点E,
∴∠D=90°-∠C=50°.故选B.
4.C [解析] A项,补充OA=OD,可利用ASA证明△AOB≌△DOC,根据全等三角形的性质可得BO=CO,进而证明△BOC是等腰三角形;
B项,补充AB=CD,可利用AAS证明△AOB≌△DOC,根据全等三角形的性质可得BO=CO,进而证明△BOC是等腰三角形;
C项,补充∠ABO=∠DCO,不能证明△AOB≌△DOC,进而不能证明△BOC是等腰三角形;
D项,补充∠ABC=∠DCB,可利用AAS证明△ABC≌△DCB,根据全等三角形的性质可得 ∠OCB=∠OBC,进而证明△BOC是等腰三角形.故选C.
5.D [解析] ∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°.
∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E=12∠ACB=30°.
连接BD,如图.
∵在等边三角形ABC中,D是AC的中点,
∴∠DBC=12∠ABC=12×60°=30°.
∴∠DBC=∠E.
∴DB=DE.
又∵DM⊥BC,
∴BM=EM,故选项B正确.
在Rt△CDM中,
∵∠DMC=90°,∠ACB=60°,
∴∠CDM=30°.
∴CM=12CD=12CE,
故选项C正确,选项D错误.
∴ME=3CM.
∴BM=3CM,故选项A正确.故选D.
6.40°或100° [解析] 当40°的内角为顶角时,这个等腰三角形的顶角为40°;当40°的内角为底角时,则该等腰三角形的另一底角为40°,∴顶角为180°-40°-40°=100°.故答案为40°或100°.
7.2 [解析] ∵D为AB的中点,AB=8 m,∴AD=4 m.∵DE⊥AC于点E,∠A=30°,
∴DE=12AD=2 m.
8.8 [解析] ∵MN∥BC,
∴∠MEB=∠EBC.
∵BE平分∠ABC,
∴∠MBE=∠EBC.
∴∠MBE=∠MEB.
∴ME=MB.
同理可得NE=NC,
∴BM+CN=ME+NE=MN=8.
9.60 [解析] ∵AD=DE,
∴∠DAE=∠DEA.
∵AB=AC,∴∠B=∠C.
设∠B=∠C=x,
则∠DAE=∠DEA=∠C+∠EDC=x+10°.
∵∠BAC+∠B+∠C=180°,
∴20°+10°+x+2x=180°,
∴x=50°,∴∠DAE=∠DEA=60°,
故∠ADE=60°.
10.50°或65°或80°或25° [解析] 要使△OAB为等腰三角形,需分四种情况讨论(如图):
①若OB1=AB1,则∠OAB=∠1=50°;
②若OA=AB2,则∠OAB=180°-2×50°=80°;
③若OA=OB3,则∠OAB=∠OBA=12(180°-50°)=65°;
若OA=OB4,则∠OAB=∠OBA=12∠1=25°.
综上所述,∠OAB的度数是50°或65°或80°或25°.
11.证明:如图,∵DE∥AC,
∴∠1=∠3.
∵AD平分∠BAC,
∴∠1=∠2.
∴∠2=∠3.
∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°.
∴∠B=∠BDE.
∴BE=DE.
故△BDE是等腰三角形.
12.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
在△ABP与△ACQ中,
AB=AC,∠ABP=∠ACQ,BP=CQ,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAP+∠PAC=∠BAC=60°,
∴∠CAQ+∠PAC=∠PAQ=60°.
又∵AP=AQ,∴△APQ是等边三角形.
13.解:(1)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=21 cm.
故答案为21.
(2)∵∠MFN=80°,
∴∠MNF+∠NMF=180°-80°=100°.
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠NMF+∠MNF=100°,
∴∠A+∠B=90°-∠AMD+90°-∠BNE=180°-100°=80°.
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°-2(∠A+∠B)=180°-2×80°=20°.
14.解:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DE∥AC,
∴∠CAD=∠ADE.
∴∠BAD=∠ADE.
∴AE=DE.
∵AD⊥DB,
∴∠ADB=90°.
∴∠BAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°.
则∠ABD=∠BDE.
∴DE=BE.
∵AB=5,
∴DE=BE=AE=12AB=2.5.
15.证明:(1)∵△ACM,△CBN都是等边三角形,
∴AC=MC,BC=NC,∠ACM=∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,
即∠ACN=∠MCB.
在△ACN和△MCB中,AC=MC,∠ACN=∠MCB,CN=CB,
∴△ACN≌△MCB(SAS),
∴AN=BM.
(2)∵△ACN≌△MCB,
∴∠CAN=∠CMB.
∵∠MCF=180°-∠ACM-∠NCB=180°-60°-60°=60°,
∴∠MCF=∠ACE.
在△CAE和△CMF中,
∠CAE=∠CMF,CA=CM,∠ACE=∠MCF,
∴△CAE≌△CMF(ASA),
∴CE=CF,
∴△CEF为等腰三角形.
又∵∠ECF=60°,
∴△CEF为等边三角形.
16.解:(1)证明:连接AD.
∵AB=AC,∠A=90°,D为BC的中点,
∴AD⊥BC,AD=12BC=BD=CD,∠B=∠C=45°,且AD平分∠BAC,
∴∠BAD=∠CAD=45°.
在△BDE和△ADF中,
BD=AD,∠B=∠DAF=45°,BE=AF,
∴△BDE≌△ADF(SAS),
∴DE=DF,∠BDE=∠ADF.
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,
即∠EDF=90°,
∴△DEF为等腰直角三角形.
(2)△DEF仍为等腰直角三角形.
证明:同(1),易证△BDE≌△ADF,
∴DF=DE,∠ADF=∠BDE.
∵∠ADF+∠FDB=90°,
∴∠BDE+∠FDB=90°,
即∠EDF=90°,
∴△DEF仍为等腰直角三角形.
一、选择题
1. 在△ABC中,∠B=50°,∠A=80°,若AB=6,则AC的长为 ( )
A.6 B.8
C.5 D.13
2.如图2,直线l分别与直线AB,CD相交于点E,F,EG平分 ∠BEF交直线CD于点G,若∠1=∠BEF,EF=3,则FG的长为 ( )
图2
A.4 B.3
C.5 D.1.5
3.如图3,在△ABC中,AB=AC,点D在CA的延长线上,DE⊥BC于点E,∠BAC=100°,则∠D的度数为 ( )
图3
A.40° B.50°
C.60° D.80°
4.如图4,AC,BD相交于点O,∠A=∠D,如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是 ( )
图4
A.OA=OD B.AB=CD
C.∠ABO=∠DCO D.∠ABC=∠DCB
5.如图5,在等边三角形ABC中,D为AC边的中点,E为BC边的延长线上一点,CE=CD,DM⊥BC于点M.下列结论错误的是 ( )
图5
A.BM=3CM B.BM=EM
C.CM=12CE D.DM=2CM
二、填空题
6.已知一个等腰三角形的一个内角为40°,则它的顶角等于 .?
7.房梁的一部分如图6所示,其中BC⊥AC,∠A=30°,AB=8 m, D是AB的中点,且DE⊥AC,垂足为E,则DE的长为 m.?
图6
8.如图7,在△ABC中,BE平分∠ABC,CE平分∠ACB,BE和CE交于点E,过点E作MN∥BC交AB于点M,交AC于点N.若MN=8,则BM+CN的长为 .?
图7
9.如图8,在△ABC中,AB=AC,D为BC上一点,且AD=DE,∠BAD=20°,∠EDC=10°,则∠ADE= °.?
图8
10.如图9,直线a,b相交于点O,∠1=50°,A是直线a上的一个定点,点B在直线b上运动,若以O,A,B为顶点的三角形是等腰三角形,则∠OAB的度数是 .?
图9
三、解答题
11.如图10,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.
求证:△BDE是等腰三角形.
图10
12.如图11,在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=
∠ACQ,BP=CQ,判断△APQ的形状,并证明.
图11
13.如图12,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,连接MC,NC,DM与EN相交于点F.
(1)若AB=21 cm,则△CMN的周长= cm;?
(2)若∠MFN=80°,求∠MCN的度数.
图12
14.如图13,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过点D作DE∥AC,交AB于点E.若AB=5,求线段DE的长.
图13
15.[2020·阜新太平区期末] 已知:如图14,C为线段AB上一点,△ACM,△CBN都是等边三角形,连接AN交MC于点E,连接BM交CN于点F,连接EF.
(1)求证:AN=BM;
(2)求证:△CEF为等边三角形.
图14
16.在△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图15,若E,F分别是AB,AC上的点,且BE=AF.求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,则△DEF是否仍为等腰直角三角形?证明你的结论.
图15
答案
1.A [解析] ∵在△ABC中,∠B=50°,∠A=80°,∴∠C=180°-∠A-∠B=180°-80°-50°=50°,
∴∠C=∠B,∴AC=AB=6.故选A.
2.B [解析] ∵EG平分∠BEF,∴∠GEB=∠GEF.∵∠1=∠BEF,∴CD∥AB,
∴∠EGF=∠GEB,∴∠GEF=∠EGF,则FG=EF=3.故选B.
3.B [解析] ∵AB=AC,∠BAC=100°,∴∠C=∠B=40°.∵DE⊥BC于点E,
∴∠D=90°-∠C=50°.故选B.
4.C [解析] A项,补充OA=OD,可利用ASA证明△AOB≌△DOC,根据全等三角形的性质可得BO=CO,进而证明△BOC是等腰三角形;
B项,补充AB=CD,可利用AAS证明△AOB≌△DOC,根据全等三角形的性质可得BO=CO,进而证明△BOC是等腰三角形;
C项,补充∠ABO=∠DCO,不能证明△AOB≌△DOC,进而不能证明△BOC是等腰三角形;
D项,补充∠ABC=∠DCB,可利用AAS证明△ABC≌△DCB,根据全等三角形的性质可得 ∠OCB=∠OBC,进而证明△BOC是等腰三角形.故选C.
5.D [解析] ∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°.
∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E=12∠ACB=30°.
连接BD,如图.
∵在等边三角形ABC中,D是AC的中点,
∴∠DBC=12∠ABC=12×60°=30°.
∴∠DBC=∠E.
∴DB=DE.
又∵DM⊥BC,
∴BM=EM,故选项B正确.
在Rt△CDM中,
∵∠DMC=90°,∠ACB=60°,
∴∠CDM=30°.
∴CM=12CD=12CE,
故选项C正确,选项D错误.
∴ME=3CM.
∴BM=3CM,故选项A正确.故选D.
6.40°或100° [解析] 当40°的内角为顶角时,这个等腰三角形的顶角为40°;当40°的内角为底角时,则该等腰三角形的另一底角为40°,∴顶角为180°-40°-40°=100°.故答案为40°或100°.
7.2 [解析] ∵D为AB的中点,AB=8 m,∴AD=4 m.∵DE⊥AC于点E,∠A=30°,
∴DE=12AD=2 m.
8.8 [解析] ∵MN∥BC,
∴∠MEB=∠EBC.
∵BE平分∠ABC,
∴∠MBE=∠EBC.
∴∠MBE=∠MEB.
∴ME=MB.
同理可得NE=NC,
∴BM+CN=ME+NE=MN=8.
9.60 [解析] ∵AD=DE,
∴∠DAE=∠DEA.
∵AB=AC,∴∠B=∠C.
设∠B=∠C=x,
则∠DAE=∠DEA=∠C+∠EDC=x+10°.
∵∠BAC+∠B+∠C=180°,
∴20°+10°+x+2x=180°,
∴x=50°,∴∠DAE=∠DEA=60°,
故∠ADE=60°.
10.50°或65°或80°或25° [解析] 要使△OAB为等腰三角形,需分四种情况讨论(如图):
①若OB1=AB1,则∠OAB=∠1=50°;
②若OA=AB2,则∠OAB=180°-2×50°=80°;
③若OA=OB3,则∠OAB=∠OBA=12(180°-50°)=65°;
若OA=OB4,则∠OAB=∠OBA=12∠1=25°.
综上所述,∠OAB的度数是50°或65°或80°或25°.
11.证明:如图,∵DE∥AC,
∴∠1=∠3.
∵AD平分∠BAC,
∴∠1=∠2.
∴∠2=∠3.
∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°.
∴∠B=∠BDE.
∴BE=DE.
故△BDE是等腰三角形.
12.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
在△ABP与△ACQ中,
AB=AC,∠ABP=∠ACQ,BP=CQ,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAP+∠PAC=∠BAC=60°,
∴∠CAQ+∠PAC=∠PAQ=60°.
又∵AP=AQ,∴△APQ是等边三角形.
13.解:(1)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=21 cm.
故答案为21.
(2)∵∠MFN=80°,
∴∠MNF+∠NMF=180°-80°=100°.
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠NMF+∠MNF=100°,
∴∠A+∠B=90°-∠AMD+90°-∠BNE=180°-100°=80°.
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°-2(∠A+∠B)=180°-2×80°=20°.
14.解:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DE∥AC,
∴∠CAD=∠ADE.
∴∠BAD=∠ADE.
∴AE=DE.
∵AD⊥DB,
∴∠ADB=90°.
∴∠BAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°.
则∠ABD=∠BDE.
∴DE=BE.
∵AB=5,
∴DE=BE=AE=12AB=2.5.
15.证明:(1)∵△ACM,△CBN都是等边三角形,
∴AC=MC,BC=NC,∠ACM=∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,
即∠ACN=∠MCB.
在△ACN和△MCB中,AC=MC,∠ACN=∠MCB,CN=CB,
∴△ACN≌△MCB(SAS),
∴AN=BM.
(2)∵△ACN≌△MCB,
∴∠CAN=∠CMB.
∵∠MCF=180°-∠ACM-∠NCB=180°-60°-60°=60°,
∴∠MCF=∠ACE.
在△CAE和△CMF中,
∠CAE=∠CMF,CA=CM,∠ACE=∠MCF,
∴△CAE≌△CMF(ASA),
∴CE=CF,
∴△CEF为等腰三角形.
又∵∠ECF=60°,
∴△CEF为等边三角形.
16.解:(1)证明:连接AD.
∵AB=AC,∠A=90°,D为BC的中点,
∴AD⊥BC,AD=12BC=BD=CD,∠B=∠C=45°,且AD平分∠BAC,
∴∠BAD=∠CAD=45°.
在△BDE和△ADF中,
BD=AD,∠B=∠DAF=45°,BE=AF,
∴△BDE≌△ADF(SAS),
∴DE=DF,∠BDE=∠ADF.
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,
即∠EDF=90°,
∴△DEF为等腰直角三角形.
(2)△DEF仍为等腰直角三角形.
证明:同(1),易证△BDE≌△ADF,
∴DF=DE,∠ADF=∠BDE.
∵∠ADF+∠FDB=90°,
∴∠BDE+∠FDB=90°,
即∠EDF=90°,
∴△DEF仍为等腰直角三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
