6.6 一次函数、一元一次方程和一元一次不等式同步练习 2021— 2022学年苏科版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 6.6 一次函数、一元一次方程和一元一次不等式同步练习 2021— 2022学年苏科版八年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 244.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 09:06:35 | ||
图片预览



文档简介
6.6 一次函数、一元一次方程和一元一次不等式
一、选择题
1.[2020·淮北濉溪县期中] 若关于x的方程4x-b=0的解为x=2,则直线y=4x-b一定经过点 ( )
A.(2,0) B.(0,3)
C.(0,4) D.(2,5)
2.[2020·济宁] 数形结合是解决数学问题常用的思想方法.如图1,直线y=x+5和直线y=ax+b相交于点P,根据图像可知,方程x+5=ax+b的解是 ( )
图1
A.x=20 B.x=5
C.x=25 D.x=15
3.[2020·乐山] 直线y=kx+b在平面直角坐标系中的位置如图2所示,则不等式kx+b≤2的解集是 ( )
图2
A.x≤-2 B.x≤-4
C.x≥-2 D.x≥-4
4.[2019·遵义] 如图3所示,直线l1:y=32x+6与直线l2:y=-52x-2交于点P(-2,3),则不等式32x+6>-52x-2的解集是 ( )
图3
A.x>-2 B.x≥-2
C.x<-2 D.x≤-2
5.[2020·成都成华区期末] 如图4,直线y=x+b和y=kx+2与x轴分别交于点A(-2,0),点B(3,0),则不等式组x+b>0,kx+2>0的解集为 ( )
图4
A.x<-2 B.x>3
C.-23
二、填空题
6.如图5,已知一次函数y=kx+b的图像,则关于x的方程kx+b=9的解为 .?
图5
7.如图6所示是一次函数y1=-2x-4和y2=x+2的图像,观察图像,回答下列问题:
图6
(1)两函数图像的交点坐标是 ;?
(2)当x 时,y1=y2;?
(3)当x 时,y1>y2;?
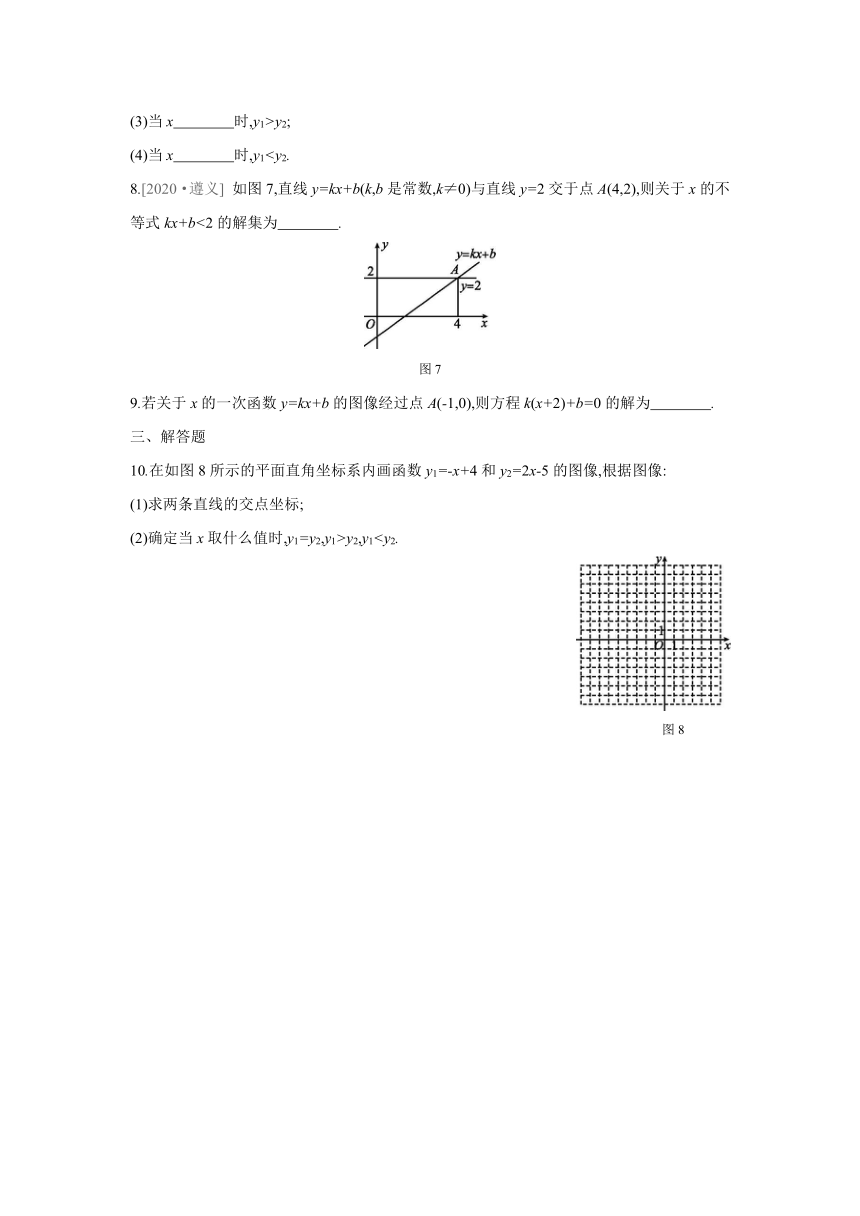
(4)当x 时,y18.[2020·遵义] 如图7,直线y=kx+b(k,b是常数,k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为 .
图7
9.若关于x的一次函数y=kx+b的图像经过点A(-1,0),则方程k(x+2)+b=0的解为 .?
三、解答题
10.在如图8所示的平面直角坐标系内画函数y1=-x+4和y2=2x-5的图像,根据图像:
(1)求两条直线的交点坐标;
(2)确定当x取什么值时,y1=y2,y1>y2,y1图8
11.[2020·百色西林县期中] 如图9,已知一次函数y1=k1x+b1的图像与一次函数y2=k2x+b2的图像交于点A,根据图像回答下列问题.
(1)求关于x的方程k1x+b1=k2x+b2的解;
(2)求出关于x的不等式k1x+b1>k2x+b2的解集;
(3)当满足什么条件时,直线y1=k1x+b1与直线y2=k2x+b2没有公共点?
图9
12.某中学八年级甲、乙两班商定举行一次远足活动,A,B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.两班同时出发,相向而行.设步行时间为x小时,甲、乙两班离A地的距离分别为y1,y2千米,y1,y2与x的函数关系图像如图10所示.根据图像解答下列问题:
(1)直接写出y1,y2与x之间的函数表达式;
(2)甲、乙两班学生出发后几小时相遇?相遇时乙班离A地多少千米?
(3)甲、乙两班首次相距4千米时,步行时间是多少小时?
图10
13.画出函数y=|x|-2的图像,利用图像回答下列问题:
(1)写出函数图像上最低点的坐标,并求出函数y的最小值;
(2)利用图像直接写出不等式|x|-2>0的解集;
(3)若函数y=kx+b(k,b为常数,且k≠0)与y=|x|-2的图像有两个交点A(m,1),B12,-32,直接写出关于x的方程|x|-2=kx+b的解.
答案
1.A [解析] 由方程可知:当x=2时,4x-b=0,即当x=2,y=0,∴直线y=4x-b一定经过点(2,0).故选A.
2.A [解析] ∵直线y=x+5和直线y=ax+b相交于点P(20,25),∴方程x+5=ax+b的解为x=20.故选A.
3.C [解析] ∵直线y=kx+b与x轴交于点(2,0),与y轴交于点(0,1),
∴2k+b=0,b=1,解得k=-12,b=1,
∴直线为y=-12x+1.
当y=2时,2=-12x+1,解得x=-2.
由图像可知,不等式kx+b≤2的解集是x≥-2.故选C.
4.A
5.C
6.x=-6 [解析] ∵一次函数y=kx+b的图像经过点(-6,9)∴当y=9时,x=-6,即方程kx+b=9的解是x=-6.
7.(1)(-2,0) (2)=-2 (3)<-2 (4)>-2
[解析] 观察图像,得交点坐标为(-2,0),即当x=-2时,y1=y2;当x<-2时,y1>y2;当x>-2时,y18.x<4 [解析] ∵直线y=kx+b与直线y=2交于点A(4,2),
∴x<4时,y<2,
∴关于x的不等式kx+b<2的解集为x<4.
9.x=-3 [解析] ∵关于x的一次函数y=kx+b的图像经过点A(-1,0),∴-k+b=0,∴b=k,
∴方程k(x+2)+b=0可化为k(x+2)+k=0,∴k(x+3)=0,∴x=-3.
10.解:如图:
(1)两条直线的交点的坐标为(3,1).
(2)由图像知,当x=3时,y1=y2;当x<3时,y1>y2;当x>3时,y111.解:(1)∵一次函数y1=k1x+b1和y2=k2x+b2的图像交于点A(3,5),
∴关于x的方程k1x+b1=k2x+b2的解为x=3.
(2)一次函数y1=k1x+b1与一次函数y2=k2x+b2的图像相交于点A(3,5),结合函数图像可知,
不等式k1x+b1>k2x+b2的解集是x<3.
(3)∵当两直线平行时,这两条直线没有公共点,∴k1=k2,b1≠b2,
∴当k1=k2,b1≠b2时,直线y1=k1x+b1与直线y2=k2x+b2没有公共点.
12.解:(1)根据图像可得,甲班2.5小时共走了10千米,则每小时走4千米,
则y1与x之间的函数表达式是y1=4x(0≤x≤2.5).
乙班从B地出发匀速步行到A地,2小时共走了10千米,则每小时走5千米,
则y2与x之间的函数表达式是y2=-5x+10(0≤x≤2).
(2)由(1)知,甲班的速度为4千米/时,乙班的速度为5千米/时.
设甲、乙两班学生出发后x小时相遇,则4x+5x=10,
解得x=109.
当x=109时,y2=-5×109+10=409,
所以甲、乙两班学生出发后109小时相遇,相遇时乙班离A地409千米.
(3)设甲、乙两班首次相距4千米时,步行时间为t小时,则5t+4t+4=10,
解得t=23.
所以甲、乙两班首次相距4千米时,步行时间是23小时.
13.解:函数y=|x|-2的图像如图所示.
(1)函数图像上最低点的坐标是(0,-2),函数y的最小值是-2.
(2)x>2或x<-2.
(3)当y=1时,|x|-2=1,
解得x=-3或x=3(舍去),
所以交点A的坐标为(-3,1),
而交点B的坐标为12,-32,
所以关于x的方程|x|-2=kx+b的解为x=-3或x=12.
一、选择题
1.[2020·淮北濉溪县期中] 若关于x的方程4x-b=0的解为x=2,则直线y=4x-b一定经过点 ( )
A.(2,0) B.(0,3)
C.(0,4) D.(2,5)
2.[2020·济宁] 数形结合是解决数学问题常用的思想方法.如图1,直线y=x+5和直线y=ax+b相交于点P,根据图像可知,方程x+5=ax+b的解是 ( )
图1
A.x=20 B.x=5
C.x=25 D.x=15
3.[2020·乐山] 直线y=kx+b在平面直角坐标系中的位置如图2所示,则不等式kx+b≤2的解集是 ( )
图2
A.x≤-2 B.x≤-4
C.x≥-2 D.x≥-4
4.[2019·遵义] 如图3所示,直线l1:y=32x+6与直线l2:y=-52x-2交于点P(-2,3),则不等式32x+6>-52x-2的解集是 ( )
图3
A.x>-2 B.x≥-2
C.x<-2 D.x≤-2
5.[2020·成都成华区期末] 如图4,直线y=x+b和y=kx+2与x轴分别交于点A(-2,0),点B(3,0),则不等式组x+b>0,kx+2>0的解集为 ( )
图4
A.x<-2 B.x>3
C.-2
二、填空题
6.如图5,已知一次函数y=kx+b的图像,则关于x的方程kx+b=9的解为 .?
图5
7.如图6所示是一次函数y1=-2x-4和y2=x+2的图像,观察图像,回答下列问题:
图6
(1)两函数图像的交点坐标是 ;?
(2)当x 时,y1=y2;?
(3)当x 时,y1>y2;?
(4)当x 时,y1
图7
9.若关于x的一次函数y=kx+b的图像经过点A(-1,0),则方程k(x+2)+b=0的解为 .?
三、解答题
10.在如图8所示的平面直角坐标系内画函数y1=-x+4和y2=2x-5的图像,根据图像:
(1)求两条直线的交点坐标;
(2)确定当x取什么值时,y1=y2,y1>y2,y1
11.[2020·百色西林县期中] 如图9,已知一次函数y1=k1x+b1的图像与一次函数y2=k2x+b2的图像交于点A,根据图像回答下列问题.
(1)求关于x的方程k1x+b1=k2x+b2的解;
(2)求出关于x的不等式k1x+b1>k2x+b2的解集;
(3)当满足什么条件时,直线y1=k1x+b1与直线y2=k2x+b2没有公共点?
图9
12.某中学八年级甲、乙两班商定举行一次远足活动,A,B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.两班同时出发,相向而行.设步行时间为x小时,甲、乙两班离A地的距离分别为y1,y2千米,y1,y2与x的函数关系图像如图10所示.根据图像解答下列问题:
(1)直接写出y1,y2与x之间的函数表达式;
(2)甲、乙两班学生出发后几小时相遇?相遇时乙班离A地多少千米?
(3)甲、乙两班首次相距4千米时,步行时间是多少小时?
图10
13.画出函数y=|x|-2的图像,利用图像回答下列问题:
(1)写出函数图像上最低点的坐标,并求出函数y的最小值;
(2)利用图像直接写出不等式|x|-2>0的解集;
(3)若函数y=kx+b(k,b为常数,且k≠0)与y=|x|-2的图像有两个交点A(m,1),B12,-32,直接写出关于x的方程|x|-2=kx+b的解.
答案
1.A [解析] 由方程可知:当x=2时,4x-b=0,即当x=2,y=0,∴直线y=4x-b一定经过点(2,0).故选A.
2.A [解析] ∵直线y=x+5和直线y=ax+b相交于点P(20,25),∴方程x+5=ax+b的解为x=20.故选A.
3.C [解析] ∵直线y=kx+b与x轴交于点(2,0),与y轴交于点(0,1),
∴2k+b=0,b=1,解得k=-12,b=1,
∴直线为y=-12x+1.
当y=2时,2=-12x+1,解得x=-2.
由图像可知,不等式kx+b≤2的解集是x≥-2.故选C.
4.A
5.C
6.x=-6 [解析] ∵一次函数y=kx+b的图像经过点(-6,9)∴当y=9时,x=-6,即方程kx+b=9的解是x=-6.
7.(1)(-2,0) (2)=-2 (3)<-2 (4)>-2
[解析] 观察图像,得交点坐标为(-2,0),即当x=-2时,y1=y2;当x<-2时,y1>y2;当x>-2时,y1
∴x<4时,y<2,
∴关于x的不等式kx+b<2的解集为x<4.
9.x=-3 [解析] ∵关于x的一次函数y=kx+b的图像经过点A(-1,0),∴-k+b=0,∴b=k,
∴方程k(x+2)+b=0可化为k(x+2)+k=0,∴k(x+3)=0,∴x=-3.
10.解:如图:
(1)两条直线的交点的坐标为(3,1).
(2)由图像知,当x=3时,y1=y2;当x<3时,y1>y2;当x>3时,y1
∴关于x的方程k1x+b1=k2x+b2的解为x=3.
(2)一次函数y1=k1x+b1与一次函数y2=k2x+b2的图像相交于点A(3,5),结合函数图像可知,
不等式k1x+b1>k2x+b2的解集是x<3.
(3)∵当两直线平行时,这两条直线没有公共点,∴k1=k2,b1≠b2,
∴当k1=k2,b1≠b2时,直线y1=k1x+b1与直线y2=k2x+b2没有公共点.
12.解:(1)根据图像可得,甲班2.5小时共走了10千米,则每小时走4千米,
则y1与x之间的函数表达式是y1=4x(0≤x≤2.5).
乙班从B地出发匀速步行到A地,2小时共走了10千米,则每小时走5千米,
则y2与x之间的函数表达式是y2=-5x+10(0≤x≤2).
(2)由(1)知,甲班的速度为4千米/时,乙班的速度为5千米/时.
设甲、乙两班学生出发后x小时相遇,则4x+5x=10,
解得x=109.
当x=109时,y2=-5×109+10=409,
所以甲、乙两班学生出发后109小时相遇,相遇时乙班离A地409千米.
(3)设甲、乙两班首次相距4千米时,步行时间为t小时,则5t+4t+4=10,
解得t=23.
所以甲、乙两班首次相距4千米时,步行时间是23小时.
13.解:函数y=|x|-2的图像如图所示.
(1)函数图像上最低点的坐标是(0,-2),函数y的最小值是-2.
(2)x>2或x<-2.
(3)当y=1时,|x|-2=1,
解得x=-3或x=3(舍去),
所以交点A的坐标为(-3,1),
而交点B的坐标为12,-32,
所以关于x的方程|x|-2=kx+b的解为x=-3或x=12.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
