第5章平面直角坐标系单元测试题 2021—2022学年苏科版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 第5章平面直角坐标系单元测试题 2021—2022学年苏科版数学八年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 221.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 09:07:27 | ||
图片预览


文档简介
第5章 平面直角坐标系
一、选择题(每小题4分,共32分)
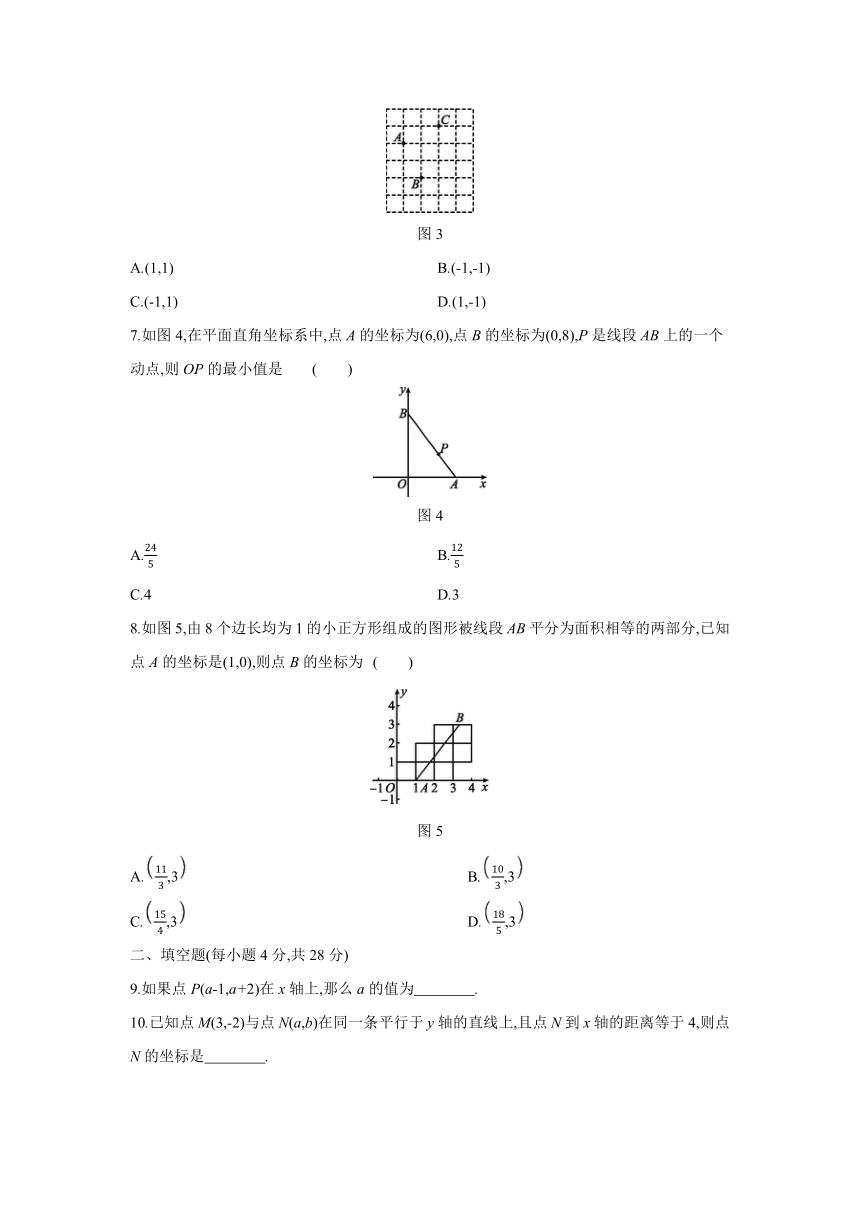
1.下列各点在第二象限的是 ( )
A.(3,2) B.(-3,-2)
C.(-3,2) D.(3,-2)
2.点M(3,1)关于x轴对称的点的坐标为 ( )
A.(-3,1) B.(3,-1)
C.(1,-3) D.(-3,-1)
3.点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度得到点A',则点A'的坐标是 ( )
A.(3,3) B.(-1,3)
C.(-1,-1) D.(3,1)
4.如图1,等边三角形OAB的边长为2,则点B的坐标为 ( )
图1
A.(1,1) B.(3,1)
C.(3,3) D.(1,3)
5.如图2,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为 ( )
图2
A.(3,1) B.(-1,1)
C.(3,5) D.(-1,5)
6.如图3所示,在正方形网格中,点A的坐标为(-1,0),点B的坐标为(0,-2),则点C的坐标为 ( )
图3
A.(1,1) B.(-1,-1)
C.(-1,1) D.(1,-1)
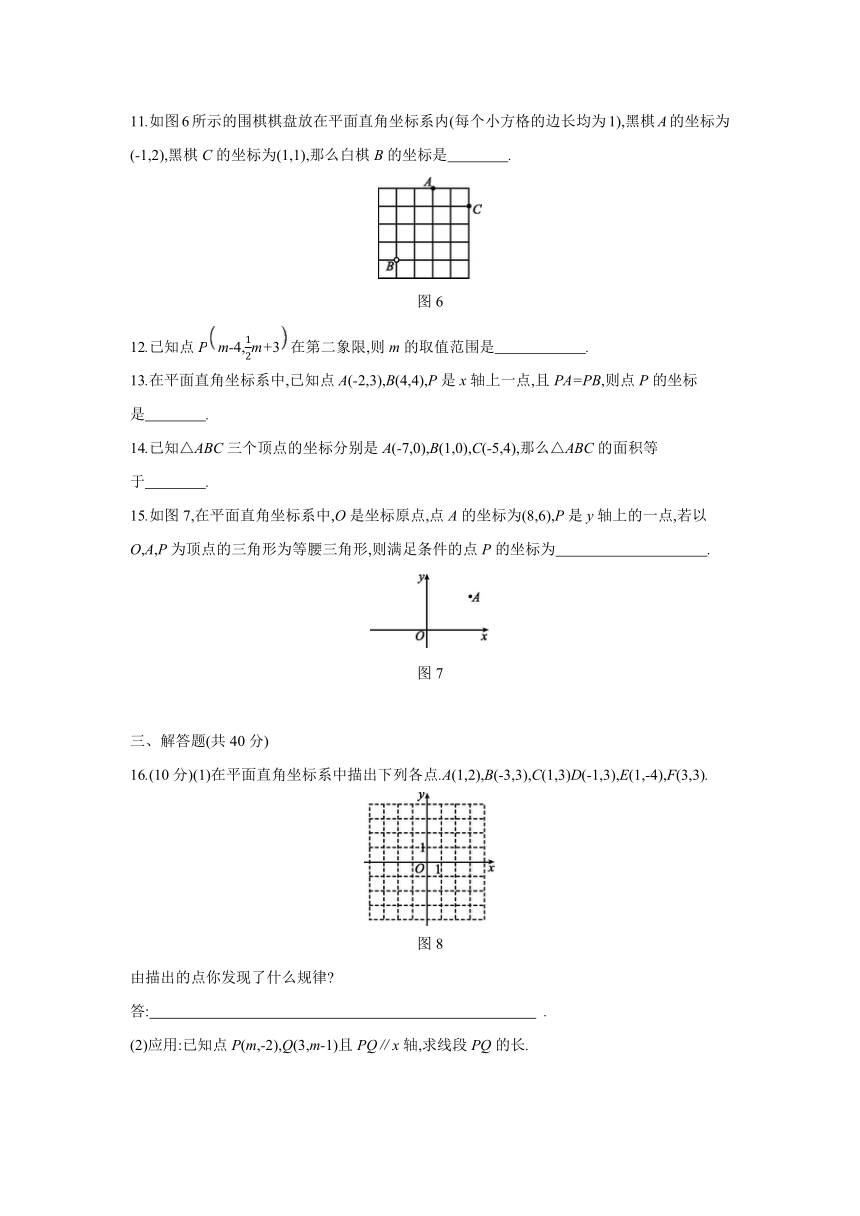
7.如图4,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,8),P是线段AB上的一个动点,则OP的最小值是 ( )
图4
A.245 B.125
C.4 D.3
8.如图5,由8个边长均为1的小正方形组成的图形被线段AB平分为面积相等的两部分,已知点A的坐标是(1,0),则点B的坐标为 ( )
图5
A.113,3 B.103,3
C.154,3 D.185,3
二、填空题(每小题4分,共28分)
9.如果点P(a-1,a+2)在x轴上,那么a的值为 .?
10.已知点M(3,-2)与点N(a,b)在同一条平行于y轴的直线上,且点N到x轴的距离等于4,则点N的坐标是 .?
11.如图6所示的围棋棋盘放在平面直角坐标系内(每个小方格的边长均为1),黑棋A的坐标为(-1,2),黑棋C的坐标为(1,1),那么白棋B的坐标是 .?
图6
12.已知点Pm-4,12m+3在第二象限,则m的取值范围是 .?
13.在平面直角坐标系中,已知点A(-2,3),B(4,4),P是x轴上一点,且PA=PB,则点P的坐标是 .?
14.已知△ABC三个顶点的坐标分别是A(-7,0),B(1,0),C(-5,4),那么△ABC的面积等于 .?
15.如图7,在平面直角坐标系中,O是坐标原点,点A的坐标为(8,6),P是y轴上的一点,若以O,A,P为顶点的三角形为等腰三角形,则满足条件的点P的坐标为 .?
图7
三、解答题(共40分)
16.(10分)(1)在平面直角坐标系中描出下列各点.A(1,2),B(-3,3),C(1,3)D(-1,3),E(1,-4),F(3,3).
图8
由描出的点你发现了什么规律?
答: .
(2)应用:已知点P(m,-2),Q(3,m-1)且PQ∥x轴,求线段PQ的长.
17.(10分)图9是学校的平面示意图,已知旗杆的坐标是(-2,3),实验室的坐标是(1,4).
(1)写出食堂、图书馆的坐标;
(2)已知办公楼的坐标是(-2,1),教学楼的坐标是(2,2),在图中标出办公楼和教学楼的位置;
(3)如果一个单位长度表示30米,请求出宿舍楼到教学楼的实际距离.
图9
18.(10分)已知A(4,0),点B在x轴上,且AB=5.
(1)直接写出点B的坐标;
(2)若点C在y轴上,且S△ABC=10,求点C的坐标;
(3)若点D(a-3,a+2),且S△ABD=15,求点D的坐标.
19.(10分)如图10,在平面直角坐标系中,长方形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)点A的坐标为 ,点B的坐标为 ;?
(2)若CD平分∠ACO交x轴于点D,求点D的坐标.
图10
答案
1.C [解析] 点(3,2)在第一象限,点(-3,-2)在第三象限,点(-3,2)在第二象限,点(3,-2)在第四象限.故选C.
2.B [解析] 关于x轴对称的两点的横坐标相等,纵坐标互为相反数.故选B.
3.D [解析] 点A向右平移2个单位长度,横坐标加上2,向下平移1个单位长度,纵坐标减去1.
4.D [解析] 如图所示,过点B作BC⊥OA于点C.
∵△OAB是等边三角形,且边长为2,∴OC=12OA=1.
在Rt△BOC中,BC=OB2-OC2=3,
∴点B的坐标为(1,3).
故选D.
5.C [解析] ∵正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,∴点B的横坐标为-1+4=3,纵坐标为1,∴点B的坐标为(3,1),∴点C的横坐标为3,纵坐标为1+4=5,∴点C的坐标为(3,5).故选C.
6.A [解析] 根据题意建立平面直角坐标系如图所示.
∴点C的坐标为(1,1).
故选A.
7.A [解析] 如图,当OP⊥AB时,OP的值最小.
∵A(6,0),B(0,8),
∴OB=8,OA=6,∴AB=10.
∵S△AOB=12OA·OB=12AB·OP,
∴OP=OA·OBAB=245.故选A.
8.A [解析] 如图,设BC=x.由题意,得12×3×(2+x)=12×8,解得x=23,∴点B的坐标为113,3.故选A.
9.-2 [解析] ∵点P(a-1,a+2)在x轴上,
∴a+2=0,解得a=-2.
10.(3,4)或(3,-4) [解析] ∵点M(3,-2)与点N(a,b)在同一条平行于y轴的直线上,∴a=3.
∵N到x轴的距离等于4,∴b=±4,∴点N的坐标为(3,4)或(3,-4).
11.(-3,-2)
12.-60,
解得-613.1912,0 [解析] 设点P的坐标为(x,0).∵PA=PB,∴(x+2)2+(0-3)2=(x-4)2+(0-4)2,解得x=1912,∴点P的坐标为1912,0.
14.16
15.(0,10)或(0,-10)或0,253或(0,12)
[解析] 如图,连接OA,则OA=82+62=10.
设P(0,m).
若OA=OP,则点P的坐标为(0,10)或(0,-10).
若OP=PA,则82+(6-m)2=m2,
解得m=253,∴P0,253.
若PA=OA,则点P的坐标为(0,12).
综上,满足条件的点P的坐标为(0,10)或(0,-10)或0,253或(0,12).
16.解:(1)如图所示.
发现的规律:纵坐标相同的点在平行于x轴的直线上,横坐标相同的点在平行于y轴的直线上.
(2)∵PQ∥x轴,∴m-1=-2,
∴m=-1,∴P(-1,-2),Q(3,-2),
∴PQ=|-1-3|=4.
17.解:(1)食堂的坐标是(-5,5),图书馆的坐标是(2,5).
(2)略.
(3)因为宿舍楼的坐标是(-6,2),教学楼的坐标是(2,2),所以宿舍楼到教学楼的实际距离是30×8=240(米).
18.解:(1)点B的坐标为(-1,0)或(9,0).
(2)∵AB=5,点C在y轴上,S△ABC=10,
∴S△ABC=12AB·OC,
∴OC=4,
∴点C坐标为(0,4)或(0,-4).
(3)∵AB=5,点D(a-3,a+2),且S△ABD=15,
∴S△ABD=12×5×|a+2|=15,∴|a+2|=6,
解得a=4或a=-8,
∴点D的坐标为(1,6)或(-11,-6).
19.解:(1)∵四边形OABC是长方形,
∴AB=OC=9,BC=OA=12,
∴A(12,0),B(12,9).
(2)如图,过点D作DM⊥AC于点M.
∵CD平分∠ACO,DO⊥CO,DM⊥AC,
∴DO=DM,∠COD=∠CMD=90°.
又∵CD=CD,
∴Rt△CDO≌△Rt△CDM(HL),
∴CM=CO=9.
∵AC=92+122=15,
∴AM=6.
设OD=DM=x.
在Rt△ADM中,
∵AD2=DM2+AM2,
∴(12-x)2=x2+62,
解得x=92,
∴D92,0.
一、选择题(每小题4分,共32分)
1.下列各点在第二象限的是 ( )
A.(3,2) B.(-3,-2)
C.(-3,2) D.(3,-2)
2.点M(3,1)关于x轴对称的点的坐标为 ( )
A.(-3,1) B.(3,-1)
C.(1,-3) D.(-3,-1)
3.点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度得到点A',则点A'的坐标是 ( )
A.(3,3) B.(-1,3)
C.(-1,-1) D.(3,1)
4.如图1,等边三角形OAB的边长为2,则点B的坐标为 ( )
图1
A.(1,1) B.(3,1)
C.(3,3) D.(1,3)
5.如图2,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为 ( )
图2
A.(3,1) B.(-1,1)
C.(3,5) D.(-1,5)
6.如图3所示,在正方形网格中,点A的坐标为(-1,0),点B的坐标为(0,-2),则点C的坐标为 ( )
图3
A.(1,1) B.(-1,-1)
C.(-1,1) D.(1,-1)
7.如图4,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,8),P是线段AB上的一个动点,则OP的最小值是 ( )
图4
A.245 B.125
C.4 D.3
8.如图5,由8个边长均为1的小正方形组成的图形被线段AB平分为面积相等的两部分,已知点A的坐标是(1,0),则点B的坐标为 ( )
图5
A.113,3 B.103,3
C.154,3 D.185,3
二、填空题(每小题4分,共28分)
9.如果点P(a-1,a+2)在x轴上,那么a的值为 .?
10.已知点M(3,-2)与点N(a,b)在同一条平行于y轴的直线上,且点N到x轴的距离等于4,则点N的坐标是 .?
11.如图6所示的围棋棋盘放在平面直角坐标系内(每个小方格的边长均为1),黑棋A的坐标为(-1,2),黑棋C的坐标为(1,1),那么白棋B的坐标是 .?
图6
12.已知点Pm-4,12m+3在第二象限,则m的取值范围是 .?
13.在平面直角坐标系中,已知点A(-2,3),B(4,4),P是x轴上一点,且PA=PB,则点P的坐标是 .?
14.已知△ABC三个顶点的坐标分别是A(-7,0),B(1,0),C(-5,4),那么△ABC的面积等于 .?
15.如图7,在平面直角坐标系中,O是坐标原点,点A的坐标为(8,6),P是y轴上的一点,若以O,A,P为顶点的三角形为等腰三角形,则满足条件的点P的坐标为 .?
图7
三、解答题(共40分)
16.(10分)(1)在平面直角坐标系中描出下列各点.A(1,2),B(-3,3),C(1,3)D(-1,3),E(1,-4),F(3,3).
图8
由描出的点你发现了什么规律?
答: .
(2)应用:已知点P(m,-2),Q(3,m-1)且PQ∥x轴,求线段PQ的长.
17.(10分)图9是学校的平面示意图,已知旗杆的坐标是(-2,3),实验室的坐标是(1,4).
(1)写出食堂、图书馆的坐标;
(2)已知办公楼的坐标是(-2,1),教学楼的坐标是(2,2),在图中标出办公楼和教学楼的位置;
(3)如果一个单位长度表示30米,请求出宿舍楼到教学楼的实际距离.
图9
18.(10分)已知A(4,0),点B在x轴上,且AB=5.
(1)直接写出点B的坐标;
(2)若点C在y轴上,且S△ABC=10,求点C的坐标;
(3)若点D(a-3,a+2),且S△ABD=15,求点D的坐标.
19.(10分)如图10,在平面直角坐标系中,长方形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)点A的坐标为 ,点B的坐标为 ;?
(2)若CD平分∠ACO交x轴于点D,求点D的坐标.
图10
答案
1.C [解析] 点(3,2)在第一象限,点(-3,-2)在第三象限,点(-3,2)在第二象限,点(3,-2)在第四象限.故选C.
2.B [解析] 关于x轴对称的两点的横坐标相等,纵坐标互为相反数.故选B.
3.D [解析] 点A向右平移2个单位长度,横坐标加上2,向下平移1个单位长度,纵坐标减去1.
4.D [解析] 如图所示,过点B作BC⊥OA于点C.
∵△OAB是等边三角形,且边长为2,∴OC=12OA=1.
在Rt△BOC中,BC=OB2-OC2=3,
∴点B的坐标为(1,3).
故选D.
5.C [解析] ∵正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,∴点B的横坐标为-1+4=3,纵坐标为1,∴点B的坐标为(3,1),∴点C的横坐标为3,纵坐标为1+4=5,∴点C的坐标为(3,5).故选C.
6.A [解析] 根据题意建立平面直角坐标系如图所示.
∴点C的坐标为(1,1).
故选A.
7.A [解析] 如图,当OP⊥AB时,OP的值最小.
∵A(6,0),B(0,8),
∴OB=8,OA=6,∴AB=10.
∵S△AOB=12OA·OB=12AB·OP,
∴OP=OA·OBAB=245.故选A.
8.A [解析] 如图,设BC=x.由题意,得12×3×(2+x)=12×8,解得x=23,∴点B的坐标为113,3.故选A.
9.-2 [解析] ∵点P(a-1,a+2)在x轴上,
∴a+2=0,解得a=-2.
10.(3,4)或(3,-4) [解析] ∵点M(3,-2)与点N(a,b)在同一条平行于y轴的直线上,∴a=3.
∵N到x轴的距离等于4,∴b=±4,∴点N的坐标为(3,4)或(3,-4).
11.(-3,-2)
12.-6
解得-6
14.16
15.(0,10)或(0,-10)或0,253或(0,12)
[解析] 如图,连接OA,则OA=82+62=10.
设P(0,m).
若OA=OP,则点P的坐标为(0,10)或(0,-10).
若OP=PA,则82+(6-m)2=m2,
解得m=253,∴P0,253.
若PA=OA,则点P的坐标为(0,12).
综上,满足条件的点P的坐标为(0,10)或(0,-10)或0,253或(0,12).
16.解:(1)如图所示.
发现的规律:纵坐标相同的点在平行于x轴的直线上,横坐标相同的点在平行于y轴的直线上.
(2)∵PQ∥x轴,∴m-1=-2,
∴m=-1,∴P(-1,-2),Q(3,-2),
∴PQ=|-1-3|=4.
17.解:(1)食堂的坐标是(-5,5),图书馆的坐标是(2,5).
(2)略.
(3)因为宿舍楼的坐标是(-6,2),教学楼的坐标是(2,2),所以宿舍楼到教学楼的实际距离是30×8=240(米).
18.解:(1)点B的坐标为(-1,0)或(9,0).
(2)∵AB=5,点C在y轴上,S△ABC=10,
∴S△ABC=12AB·OC,
∴OC=4,
∴点C坐标为(0,4)或(0,-4).
(3)∵AB=5,点D(a-3,a+2),且S△ABD=15,
∴S△ABD=12×5×|a+2|=15,∴|a+2|=6,
解得a=4或a=-8,
∴点D的坐标为(1,6)或(-11,-6).
19.解:(1)∵四边形OABC是长方形,
∴AB=OC=9,BC=OA=12,
∴A(12,0),B(12,9).
(2)如图,过点D作DM⊥AC于点M.
∵CD平分∠ACO,DO⊥CO,DM⊥AC,
∴DO=DM,∠COD=∠CMD=90°.
又∵CD=CD,
∴Rt△CDO≌△Rt△CDM(HL),
∴CM=CO=9.
∵AC=92+122=15,
∴AM=6.
设OD=DM=x.
在Rt△ADM中,
∵AD2=DM2+AM2,
∴(12-x)2=x2+62,
解得x=92,
∴D92,0.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
