第11章《反比例函数》单元试卷 2020-2021学年苏科版 八年级下册数学 (Word版 含答案)
文档属性
| 名称 | 第11章《反比例函数》单元试卷 2020-2021学年苏科版 八年级下册数学 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 09:12:24 | ||
图片预览

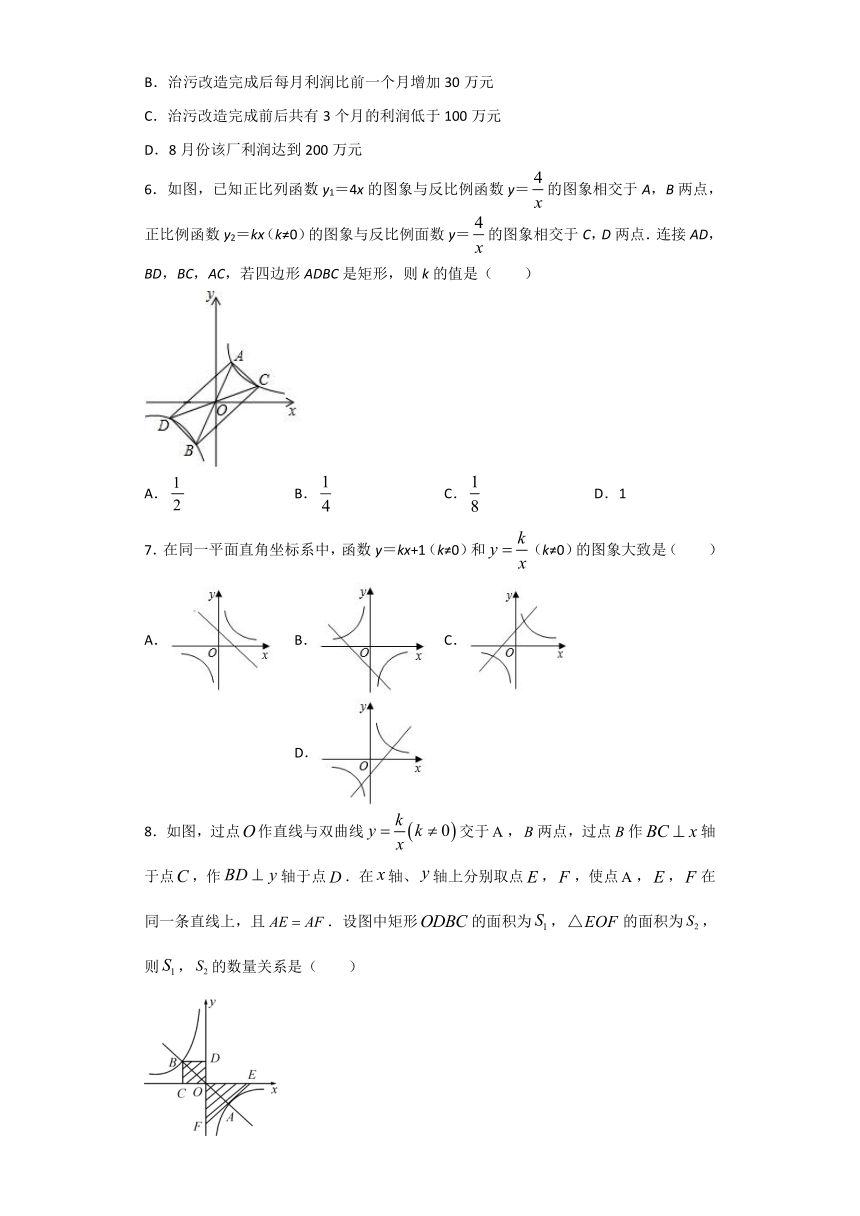

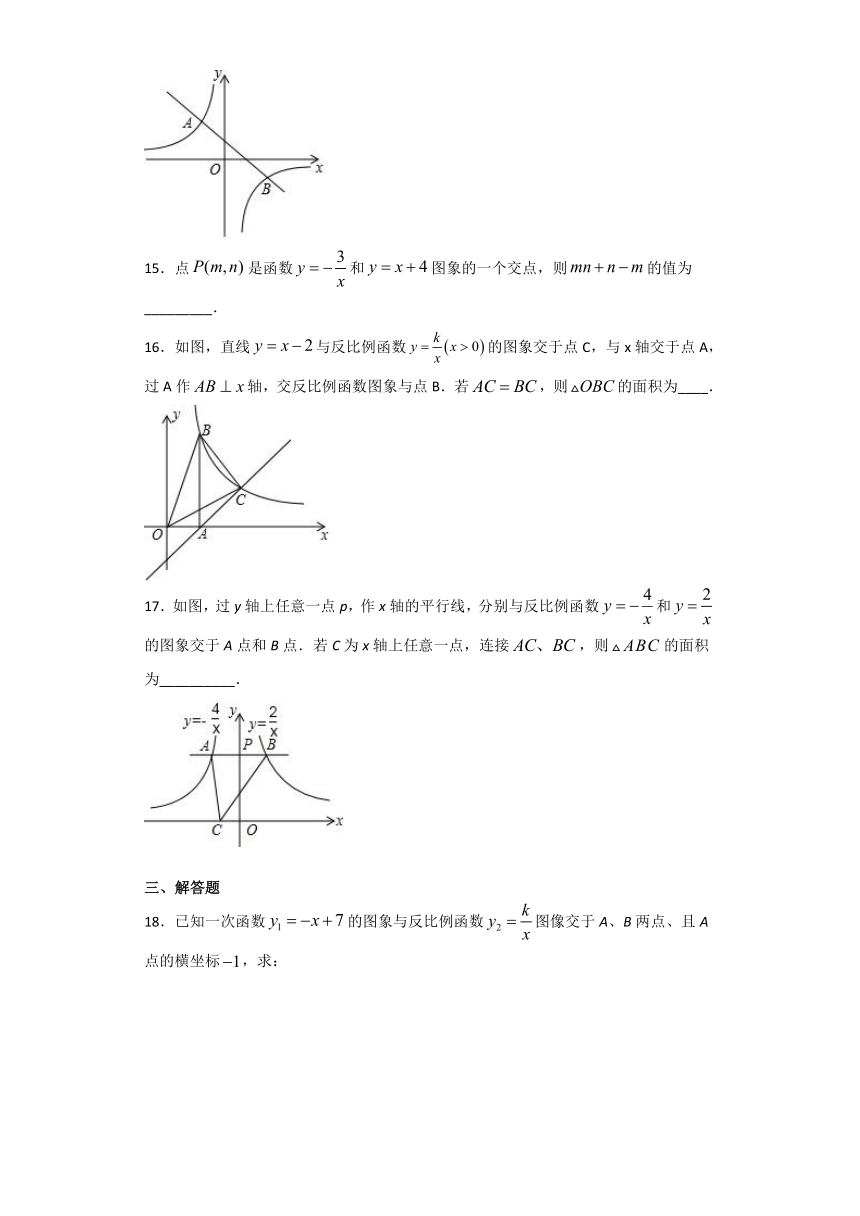

文档简介
八年级下册数学第11章《反比例函数》单元试卷-2020-2021年苏科版数学
一、单选题
1.函数是反比例函数,则a的值是( )
A. B.1 C. D.
2.已知都在反比例函数的图象上,则的大小关系的是( )
A. B. C. D.
3.如图,M是反比例函数的图象上的任意一点,轴于点N,且的面积为2,则k的值是( )
A.2 B. C.4 D.
4.若A(x1,y1)、B(x2,y2)两点在反比例函数y=的图象上,①过点B作BC⊥x轴,C为垂足,连接OB.若△BCO的面积为2,则k=9;②若x1=2x2,则2y1﹣y2=0;③若y1<0<y2,且x1>x2,则k>5其中真命题个数是( )
A.0 B.1 C.2 D.3
5.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有3个月的利润低于100万元
D.8月份该厂利润达到200万元
6.如图,已知正比列函数y1=4x的图象与反比例函数y=的图象相交于A,B两点,正比例函数y2=kx(k≠0)的图象与反比例面数y=的图象相交于C,D两点.连接AD,BD,BC,AC,若四边形ADBC是矩形,则k的值是( )
A. B. C. D.1
7.在同一平面直角坐标系中,函数y=kx+1(k≠0)和(k≠0)的图象大致是( )
A. B. C. D.
8.如图,过点作直线与双曲线交于,两点,过点作轴于点,作轴于点.在轴、轴上分别取点,,使点,,在同一条直线上,且.设图中矩形的面积为,的面积为,则,的数量关系是( )
A. B. C. D.
9.如图,一次函数与反比例函数分别交于两点,则不等式的解集是( )
A. B. C.或 D.
10.如图,在平面直角坐标系中,四边形是矩形,∥轴,且点C的坐标为,,.将矩形向右平移,得矩形使点,恰好同时落在反比例函数的图象上,则反比例函数的解析式为( )
A. B. C. D.
二、填空题
11.函数中自变量x的取值范围是__________.
12.已知菱形的面积是12cm2,菱形的两条对角线长分别为和,则与之间的函数关系是________________.
13.已知反比例函数的图像上有两点,,那么______.(填“>”或“<”)
14.如图,反比例函数y1=和一次函数y2=ax+b的图象交于点A(﹣1,2),B(2,﹣1)两点,则当﹣2<y1<y2<时,x的取值范围为_____.
15.点是函数和图象的一个交点,则的值为_________.
16.如图,直线与反比例函数的图象交于点C,与x轴交于点A,过A作轴,交反比例函数图象与点B.若,则的面积为____.
17.如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为__________.
三、解答题
18.已知一次函数的图象与反比例函数图像交于A、B两点、且A点的横坐标,求:
(1)反比例函数的解析式.
(2)的面积.
(3)直接写出满足时x的取值范围.
19.已知一次函数与反比例函数的图象交于点,.
(1)求这两个函效的表达式;
(2)直接写出关于x的不等式的解;
(3)若点在一次函数的图象上,若点在反比例函数的图象上,,请比较与的大小.
20.(本题满分8分)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,=16000Pa.
(1)当V =1.2m3时,求的值:
(2)当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
21.实验数据显示,一般成人喝50毫升某品牌白酒后,血液中酒精含量y(毫克/百毫升)与时间x(时)变化的图象,如下图(图象由线段OA与部分双曲线AB组成) .国家规定,车辆驾驶人员血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线AB的函数解析式;
(2)参照上述数学模型,假设某驾驶员晚上22:30在家喝完50毫升该品牌白酒,第二天早上7:00能否驾车去上班?请说明理由.
22.如图,在平面直角坐标系中,点在反比例函数的图像上,点B在射线上,轴,垂足为C,与反比例函数的图像相交于点D,连接,.
(1)当点B的横坐标为6时,求线段的长;
(2)若,求点的坐标.
23.如图,在平面直角坐标系中,四边形为正方形,已知点,点B、C在二象限内.
(1)点B的坐标________;
(2)将正方形以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B,D两点的对应点B、D正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图象上的点Q,使得以P、Q、B、D四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标:若不存在,请说明理由.
参考答案
1.A
解:∵函数是反比例函数,
∴,,
解得:a=-1,
故选A.
2.A
解:∵k=2>0,
∴图象在一、三象限,且在每一象限内y随x的增大而减小.
∵1<2,
∴y1>y2>0,
∵-3<0,
∴y3<0,
∴y1>y2>y3,
3.D
解:∵反比例函数的图象在二、四象限,
∴k<0,
∵点M是该函数图象上一点,S△MON=2,
,解得k=4(舍)或-4.
故选:D.
4.B
解:∵A(x1,y1)、B(x2,y2)两点在反比例函数y=的图象上,
∴过点B作BC⊥x轴,C为垂足,连接OB.若△BCO的面积为2,则|k﹣5|=2×2,得k=9或k=1,故①中的命题是假命题;
若x1=2x2,则y2=2y1,故2y1﹣y2=0,故②中的命题是真命题;
若y1<0<y2,且x1>x2,则k﹣5<0,故k<5,故③中的命题是假命题.
故选:B.
5.D
解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项正确,不符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x-70,
故y=200时,200=30x-70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项不正确,符合题意.
故选:C.
6.B
【详解】
解:联立y1=4x和y=得: ,
解得:或,
故点A(1,4),
联立y2=kx(k≠0)和y=,同理可得,点C(,2),
∵四边形ADBC是矩形,故OA=OC,
即()2+(2)2=12+42,
解得:k=,
故选:B.
7.C
①当k>?0时,y=kx+1过第一、二、三象限,过第一、三象限;
②当k<0时,y=?kx+1过第一、二、四象限,过第二、四象限,
观察图形可知,只有C选项符合题意,
故选:C.
8.B
解:过点A作AM⊥x轴于点M,如图所示.
∵AM⊥x轴,BC⊥x轴,BD⊥y轴,
∴S矩形ODBC=-k,S△AOM=-k.
∵AE=AF.OF⊥x轴,AM⊥x轴,
∴AM=OF,ME=OM=OE,
∴S△EOF=OE?OF=4S△AOM=-2k,
∴2S矩形ODBC=S△EOF,
即2S1=S2.
故答案为:2S1=S2.
9.C
解:观察函数图象,发现:
当或时,一次函数图象在反比例函数图象的下方,
∴不等式的解集是或.
故选:C.
10.C
解: 点C的坐标为,,,
,
设点,,
点,在反比例函数的图象上,
k==,
解得,a=6,
,
故选:C.
11.x≠5
根据题意得,5?x≠0, 则x≠5.
故答案为x≠5.
【点睛】
本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数解析式是整式时,自变量可取全体实数;(2)当函数解析式是分式时,分式的分母不能为0;(3)当函数解析式是二次根式时,被开方数非负.
12.
解:由题意得:xy=12,可得:,
故答案为:.
13.
,
反比例函数的图象在每一个象限内y随着x的增大而减小,
,
,
故答案为:.
14.1<x<2
解:∵反比例函数y1=和一次函数y2=ax+b的图象交于点A(﹣1,2),B(2,﹣1)两点,
∴k=﹣1×2=﹣2,
∴反比例函数为y=﹣,
把y=﹣2代入求得x=1;
∴由图可得,当﹣2<y1<y2<时,x的取值范围是1<x<2,
故答案为1<x<2.
15.
解:∵点P(m,n)是函数和y=x+4图象的一个交点,
∴mn=-3,n=m+4,
∴n-m=4,
∴mn+n-m=-3+4=1,
故答案为:1.
16.6
解:作于,如图,
把代入得,解得,则点坐标为,
把代入得,则点坐标为,
,
,
点的纵坐标为,
把代入得,则点坐标为,
把代入得,解得,
点坐标为,点坐标为,
.
故答案为6.
17.3
解:设,
直线轴,
,两点的纵坐标都为,而点在反比例函数的图象上,
当,,即点坐标为,,
又点在反比例函数的图象上,
当,,即点坐标为,,
,
.
故答案为:3.
18.
解:(1)把x=-1分别代入y1=-x+7得y1=1+7=8,
∴A(-1,8),
把A(-1,8)代入得,
解得 k=-8,
∴反比例函数的解析式为;
(2)设y=-x+7与y轴交点为C(0,7)
∴OC=7,
联立得,解得或,
∴B(8,-1),
∴S△AOB=S△AOC+S△BOC=;
(3)y1<y2时x的取值范围是-1<x<0或x>8.
19.
解:(1)把代入得,
反比例函数解析式为,
把代入得,解得,则,,
把,,代入得,解得,
一次函数解析式为;
(2)由图可知:
不等式的解集为或;
(3),
,
.
20.(1)20000Pa;(2)
【详解】
解:(1)设函数解析式为P=,
∵当V=1.5m3时,p=16000Pa,
∴k=Vp=24000,
∴,
当v=1.2 m3时,p=20000(Pa);
(3)∵气球内的气压大于40000Pa时,气球将爆炸,
∴≤4000,
解得:v≥0.6,
即气球的体积应不小于0.6m3.
21.解:(1)依题意,直线过,,则直线的解析式为,
当时,,即,,
设双曲线的解析式为,将点,代入得:,
;
由得当时,,
从晚上到第二天早上时间间距为8.5小时,
,
第二天早上不能驾车去上班.
22.(1);(2)(18,12)或
解:(1)将点代入反比例函数中,
∴反比例函数解析式为:
设射线OA的解析式为:
将点代入中,,解得:
∴射线OA的解析式为:
在中,当x=6时,y=4
∴B点坐标为(6,4)
在中,当x=6时,y=1
∴D点坐标为(6,1)
过点A作AE⊥BC
∵,B(6,4),D(6,1)
∴AE=3,DE=1
在Rt△ADE中,
(2)设B点坐标为(x,),
∴D点坐标为(x,)
∴
解得:;
∴B点坐标为(18,12)或
23.解:(1)如图,
过点B、D分别作BH⊥x轴、DG⊥x轴交于点H、G,
∵点A(-6,0)、D(-7,3),
∴OA=6,OG=7,DG=3,
∴AG=OG-OA=1,
∵∠DAG+∠BAH=90°,∠DAG+∠GDA=90°,
∴∠GDA=∠BAH,
又∠DGA=∠AHB=90°,AD=AB,
∴△DGA≌△AHB(AAS),
∴DG=AH=3,BH=AG=1,
∴点B坐标为(-3,1);
(2)由(1)知,B(-3,1),
∵D(-7,3)
∴运动t秒时,点D'(-7+2t,3)、B'(-3+2t,1),
设反比例函数解析式为,
∵点B',D'在反比例函数图象上,
∴k=(-7+2t)×3=(-3+2t)×1,
∴,
∴反比例函数解析式为;
(3)存在,理由:
由(2)知,点D'(-7+2t,3)、B'(-3+2t,1),,
∴D'(2,3)、B'(6,1),
由(2)知,反比例函数解析式为,
设点,点P(0,s),
以P、Q、B'、D'四个点为顶点的四边形是平行四边形,
∴①当PQ与B'D'是对角线时,
∴,
∴,
∴,
②当PB'与QD'是对角线时,
∴,
∴,
∴,
③当PD'与QB'是对角线时,
∴,
∴,
∴,
综上所述:或或.
一、单选题
1.函数是反比例函数,则a的值是( )
A. B.1 C. D.
2.已知都在反比例函数的图象上,则的大小关系的是( )
A. B. C. D.
3.如图,M是反比例函数的图象上的任意一点,轴于点N,且的面积为2,则k的值是( )
A.2 B. C.4 D.
4.若A(x1,y1)、B(x2,y2)两点在反比例函数y=的图象上,①过点B作BC⊥x轴,C为垂足,连接OB.若△BCO的面积为2,则k=9;②若x1=2x2,则2y1﹣y2=0;③若y1<0<y2,且x1>x2,则k>5其中真命题个数是( )
A.0 B.1 C.2 D.3
5.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有3个月的利润低于100万元
D.8月份该厂利润达到200万元
6.如图,已知正比列函数y1=4x的图象与反比例函数y=的图象相交于A,B两点,正比例函数y2=kx(k≠0)的图象与反比例面数y=的图象相交于C,D两点.连接AD,BD,BC,AC,若四边形ADBC是矩形,则k的值是( )
A. B. C. D.1
7.在同一平面直角坐标系中,函数y=kx+1(k≠0)和(k≠0)的图象大致是( )
A. B. C. D.
8.如图,过点作直线与双曲线交于,两点,过点作轴于点,作轴于点.在轴、轴上分别取点,,使点,,在同一条直线上,且.设图中矩形的面积为,的面积为,则,的数量关系是( )
A. B. C. D.
9.如图,一次函数与反比例函数分别交于两点,则不等式的解集是( )
A. B. C.或 D.
10.如图,在平面直角坐标系中,四边形是矩形,∥轴,且点C的坐标为,,.将矩形向右平移,得矩形使点,恰好同时落在反比例函数的图象上,则反比例函数的解析式为( )
A. B. C. D.
二、填空题
11.函数中自变量x的取值范围是__________.
12.已知菱形的面积是12cm2,菱形的两条对角线长分别为和,则与之间的函数关系是________________.
13.已知反比例函数的图像上有两点,,那么______.(填“>”或“<”)
14.如图,反比例函数y1=和一次函数y2=ax+b的图象交于点A(﹣1,2),B(2,﹣1)两点,则当﹣2<y1<y2<时,x的取值范围为_____.
15.点是函数和图象的一个交点,则的值为_________.
16.如图,直线与反比例函数的图象交于点C,与x轴交于点A,过A作轴,交反比例函数图象与点B.若,则的面积为____.
17.如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数和的图象交于A点和B点.若C为x轴上任意一点,连接,则的面积为__________.
三、解答题
18.已知一次函数的图象与反比例函数图像交于A、B两点、且A点的横坐标,求:
(1)反比例函数的解析式.
(2)的面积.
(3)直接写出满足时x的取值范围.
19.已知一次函数与反比例函数的图象交于点,.
(1)求这两个函效的表达式;
(2)直接写出关于x的不等式的解;
(3)若点在一次函数的图象上,若点在反比例函数的图象上,,请比较与的大小.
20.(本题满分8分)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,=16000Pa.
(1)当V =1.2m3时,求的值:
(2)当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
21.实验数据显示,一般成人喝50毫升某品牌白酒后,血液中酒精含量y(毫克/百毫升)与时间x(时)变化的图象,如下图(图象由线段OA与部分双曲线AB组成) .国家规定,车辆驾驶人员血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线AB的函数解析式;
(2)参照上述数学模型,假设某驾驶员晚上22:30在家喝完50毫升该品牌白酒,第二天早上7:00能否驾车去上班?请说明理由.
22.如图,在平面直角坐标系中,点在反比例函数的图像上,点B在射线上,轴,垂足为C,与反比例函数的图像相交于点D,连接,.
(1)当点B的横坐标为6时,求线段的长;
(2)若,求点的坐标.
23.如图,在平面直角坐标系中,四边形为正方形,已知点,点B、C在二象限内.
(1)点B的坐标________;
(2)将正方形以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B,D两点的对应点B、D正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图象上的点Q,使得以P、Q、B、D四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标:若不存在,请说明理由.
参考答案
1.A
解:∵函数是反比例函数,
∴,,
解得:a=-1,
故选A.
2.A
解:∵k=2>0,
∴图象在一、三象限,且在每一象限内y随x的增大而减小.
∵1<2,
∴y1>y2>0,
∵-3<0,
∴y3<0,
∴y1>y2>y3,
3.D
解:∵反比例函数的图象在二、四象限,
∴k<0,
∵点M是该函数图象上一点,S△MON=2,
,解得k=4(舍)或-4.
故选:D.
4.B
解:∵A(x1,y1)、B(x2,y2)两点在反比例函数y=的图象上,
∴过点B作BC⊥x轴,C为垂足,连接OB.若△BCO的面积为2,则|k﹣5|=2×2,得k=9或k=1,故①中的命题是假命题;
若x1=2x2,则y2=2y1,故2y1﹣y2=0,故②中的命题是真命题;
若y1<0<y2,且x1>x2,则k﹣5<0,故k<5,故③中的命题是假命题.
故选:B.
5.D
解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项正确,不符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x-70,
故y=200时,200=30x-70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项不正确,符合题意.
故选:C.
6.B
【详解】
解:联立y1=4x和y=得: ,
解得:或,
故点A(1,4),
联立y2=kx(k≠0)和y=,同理可得,点C(,2),
∵四边形ADBC是矩形,故OA=OC,
即()2+(2)2=12+42,
解得:k=,
故选:B.
7.C
①当k>?0时,y=kx+1过第一、二、三象限,过第一、三象限;
②当k<0时,y=?kx+1过第一、二、四象限,过第二、四象限,
观察图形可知,只有C选项符合题意,
故选:C.
8.B
解:过点A作AM⊥x轴于点M,如图所示.
∵AM⊥x轴,BC⊥x轴,BD⊥y轴,
∴S矩形ODBC=-k,S△AOM=-k.
∵AE=AF.OF⊥x轴,AM⊥x轴,
∴AM=OF,ME=OM=OE,
∴S△EOF=OE?OF=4S△AOM=-2k,
∴2S矩形ODBC=S△EOF,
即2S1=S2.
故答案为:2S1=S2.
9.C
解:观察函数图象,发现:
当或时,一次函数图象在反比例函数图象的下方,
∴不等式的解集是或.
故选:C.
10.C
解: 点C的坐标为,,,
,
设点,,
点,在反比例函数的图象上,
k==,
解得,a=6,
,
故选:C.
11.x≠5
根据题意得,5?x≠0, 则x≠5.
故答案为x≠5.
【点睛】
本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数解析式是整式时,自变量可取全体实数;(2)当函数解析式是分式时,分式的分母不能为0;(3)当函数解析式是二次根式时,被开方数非负.
12.
解:由题意得:xy=12,可得:,
故答案为:.
13.
,
反比例函数的图象在每一个象限内y随着x的增大而减小,
,
,
故答案为:.
14.1<x<2
解:∵反比例函数y1=和一次函数y2=ax+b的图象交于点A(﹣1,2),B(2,﹣1)两点,
∴k=﹣1×2=﹣2,
∴反比例函数为y=﹣,
把y=﹣2代入求得x=1;
∴由图可得,当﹣2<y1<y2<时,x的取值范围是1<x<2,
故答案为1<x<2.
15.
解:∵点P(m,n)是函数和y=x+4图象的一个交点,
∴mn=-3,n=m+4,
∴n-m=4,
∴mn+n-m=-3+4=1,
故答案为:1.
16.6
解:作于,如图,
把代入得,解得,则点坐标为,
把代入得,则点坐标为,
,
,
点的纵坐标为,
把代入得,则点坐标为,
把代入得,解得,
点坐标为,点坐标为,
.
故答案为6.
17.3
解:设,
直线轴,
,两点的纵坐标都为,而点在反比例函数的图象上,
当,,即点坐标为,,
又点在反比例函数的图象上,
当,,即点坐标为,,
,
.
故答案为:3.
18.
解:(1)把x=-1分别代入y1=-x+7得y1=1+7=8,
∴A(-1,8),
把A(-1,8)代入得,
解得 k=-8,
∴反比例函数的解析式为;
(2)设y=-x+7与y轴交点为C(0,7)
∴OC=7,
联立得,解得或,
∴B(8,-1),
∴S△AOB=S△AOC+S△BOC=;
(3)y1<y2时x的取值范围是-1<x<0或x>8.
19.
解:(1)把代入得,
反比例函数解析式为,
把代入得,解得,则,,
把,,代入得,解得,
一次函数解析式为;
(2)由图可知:
不等式的解集为或;
(3),
,
.
20.(1)20000Pa;(2)
【详解】
解:(1)设函数解析式为P=,
∵当V=1.5m3时,p=16000Pa,
∴k=Vp=24000,
∴,
当v=1.2 m3时,p=20000(Pa);
(3)∵气球内的气压大于40000Pa时,气球将爆炸,
∴≤4000,
解得:v≥0.6,
即气球的体积应不小于0.6m3.
21.解:(1)依题意,直线过,,则直线的解析式为,
当时,,即,,
设双曲线的解析式为,将点,代入得:,
;
由得当时,,
从晚上到第二天早上时间间距为8.5小时,
,
第二天早上不能驾车去上班.
22.(1);(2)(18,12)或
解:(1)将点代入反比例函数中,
∴反比例函数解析式为:
设射线OA的解析式为:
将点代入中,,解得:
∴射线OA的解析式为:
在中,当x=6时,y=4
∴B点坐标为(6,4)
在中,当x=6时,y=1
∴D点坐标为(6,1)
过点A作AE⊥BC
∵,B(6,4),D(6,1)
∴AE=3,DE=1
在Rt△ADE中,
(2)设B点坐标为(x,),
∴D点坐标为(x,)
∴
解得:;
∴B点坐标为(18,12)或
23.解:(1)如图,
过点B、D分别作BH⊥x轴、DG⊥x轴交于点H、G,
∵点A(-6,0)、D(-7,3),
∴OA=6,OG=7,DG=3,
∴AG=OG-OA=1,
∵∠DAG+∠BAH=90°,∠DAG+∠GDA=90°,
∴∠GDA=∠BAH,
又∠DGA=∠AHB=90°,AD=AB,
∴△DGA≌△AHB(AAS),
∴DG=AH=3,BH=AG=1,
∴点B坐标为(-3,1);
(2)由(1)知,B(-3,1),
∵D(-7,3)
∴运动t秒时,点D'(-7+2t,3)、B'(-3+2t,1),
设反比例函数解析式为,
∵点B',D'在反比例函数图象上,
∴k=(-7+2t)×3=(-3+2t)×1,
∴,
∴反比例函数解析式为;
(3)存在,理由:
由(2)知,点D'(-7+2t,3)、B'(-3+2t,1),,
∴D'(2,3)、B'(6,1),
由(2)知,反比例函数解析式为,
设点,点P(0,s),
以P、Q、B'、D'四个点为顶点的四边形是平行四边形,
∴①当PQ与B'D'是对角线时,
∴,
∴,
∴,
②当PB'与QD'是对角线时,
∴,
∴,
∴,
③当PD'与QB'是对角线时,
∴,
∴,
∴,
综上所述:或或.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
