2020--2021学年沪科版八年级数学下册第18章 勾股定理: 折叠专题(Word版 含答案)
文档属性
| 名称 | 2020--2021学年沪科版八年级数学下册第18章 勾股定理: 折叠专题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 180.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 10:37:46 | ||
图片预览


文档简介
2021年沪科版八年级下折叠专题(含答案)
一、计算题
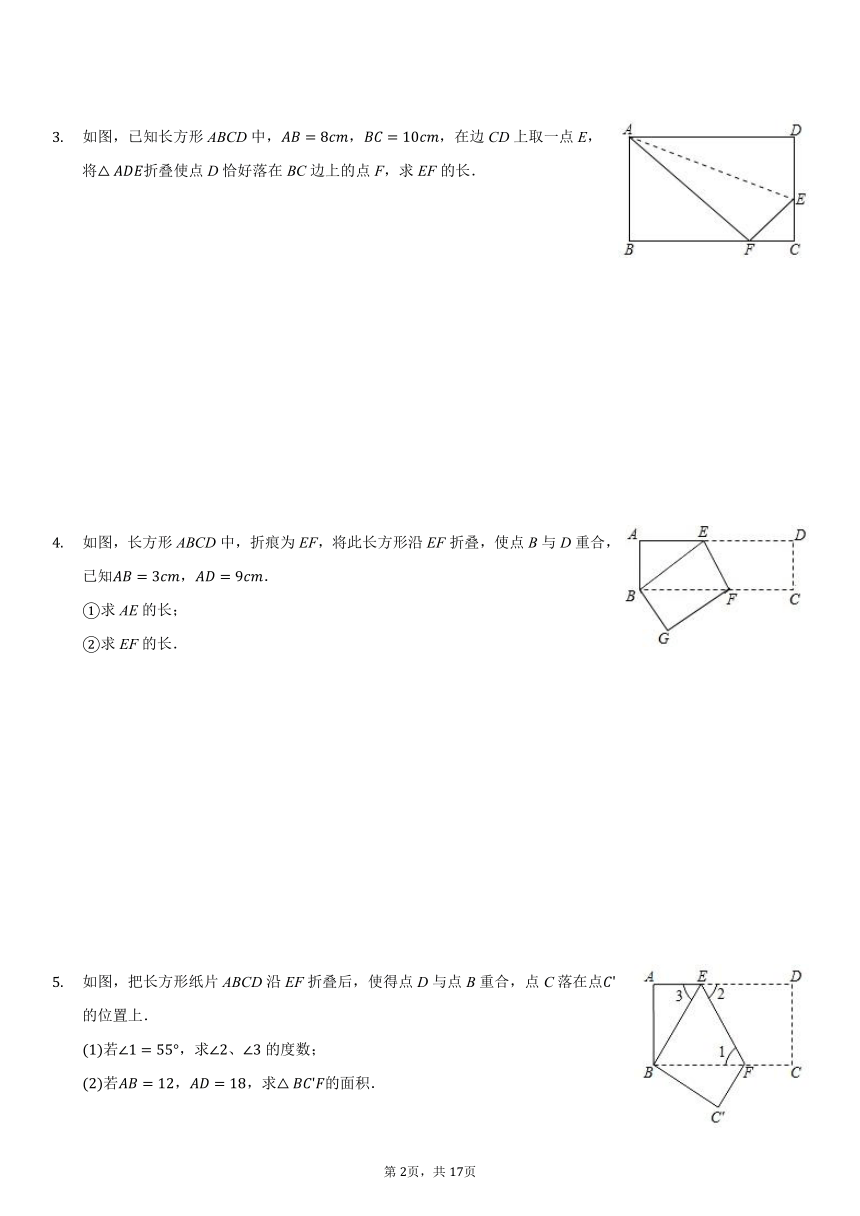
如图,长方形ABCD放在平面直角坐标系中,B点与原点重合.AB在y轴正半轴上已D点坐标为为(10,8).当AD沿一直线折叠时,顶点D落在BC边上的点F处(折痕为AE).请你求出点F和点E的坐标.
如图,长方形纸片ABCD,AD//BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF.
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
如图,已知长方形ABCD中,AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求EF的长.
如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与D重合,已知AB=3cm,AD=9cm.
①求AE的长;
②求EF的长.
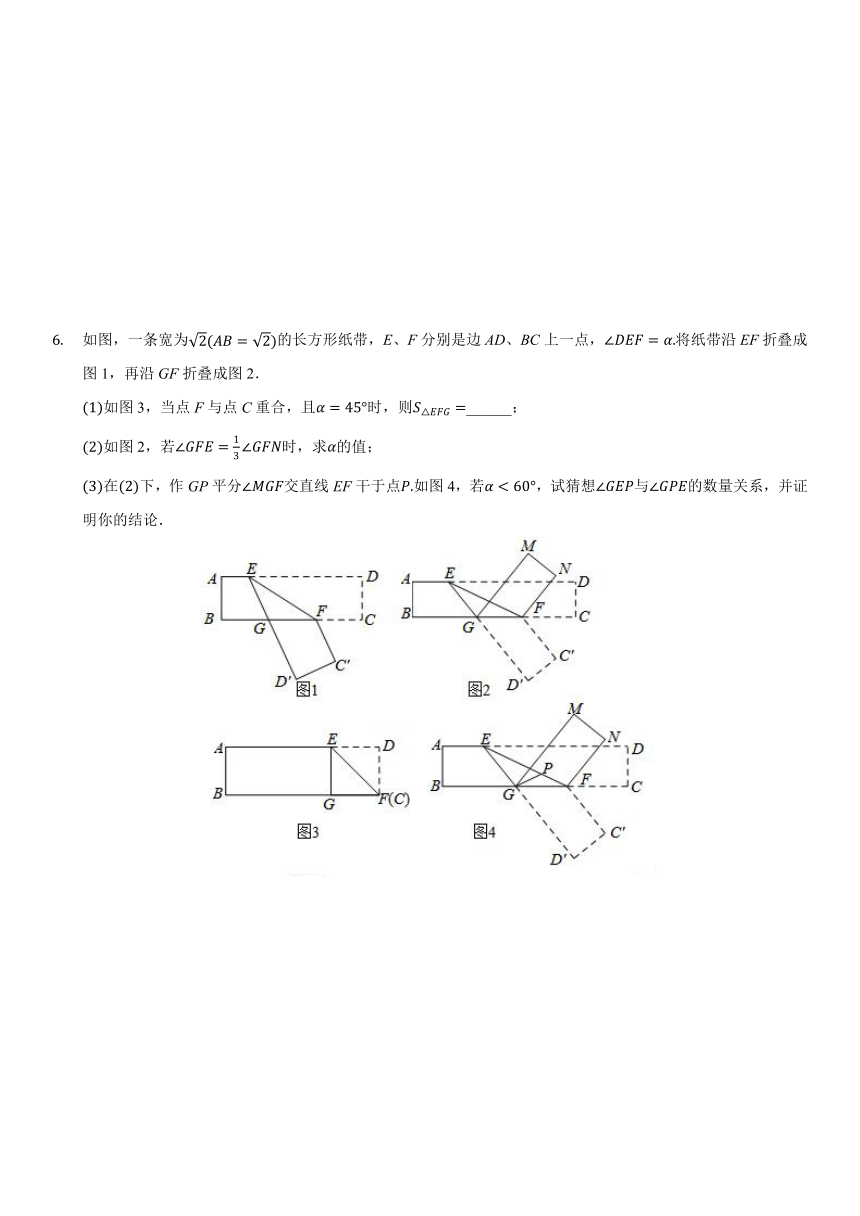
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C'的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC'F的面积.
如图,一条宽为2(AB=2)的长方形纸带,E、F分别是边AD、BC上一点,∠DEF=α.将纸带沿EF折叠成图1,再沿GF折叠成图2.
(1)如图3,当点F与点C重合,且α=45°时,则S△EFG=______;
(2)如图2,若∠GFE=13∠GFN时,求α的值;
(3)在(2)下,作GP平分∠MGF交直线EF干于点P.如图4,若α<60°,试猜想∠GEP与∠GPE的数量关系,并证明你的结论.
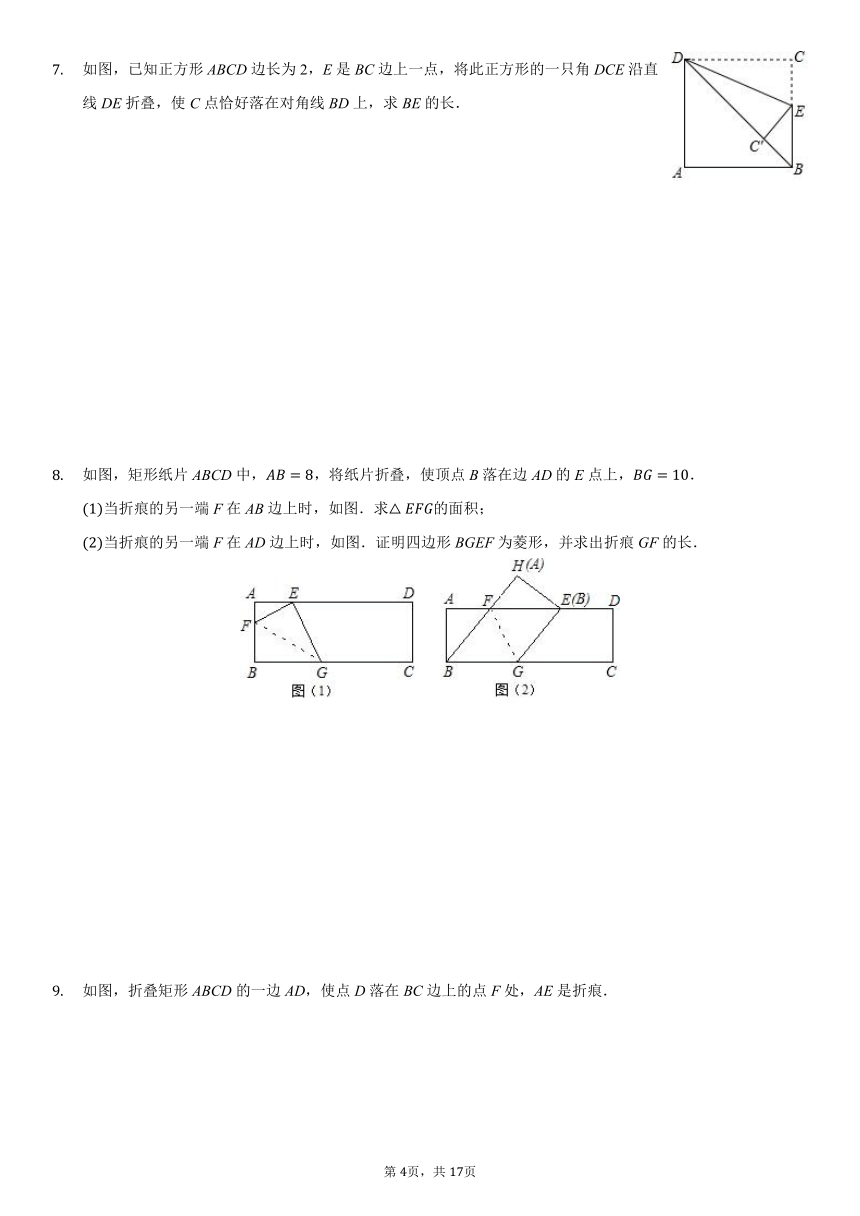
如图,已知正方形ABCD边长为2,E是BC边上一点,将此正方形的一只角DCE沿直线DE折叠,使C点恰好落在对角线BD上,求BE的长.
如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10.
(1)当折痕的另一端F在AB边上时,如图.求△EFG的面积;
(2)当折痕的另一端F在AD边上时,如图.证明四边形BGEF为菱形,并求出折痕GF的长.
如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,AE是折痕.
(1)如图1,若AB=4,AD=5,求折痕AE的长;
(2)如图2,若AE=,且EC:FC=3:4,求矩形ABCD的周长.
如图,矩形ABCD中,AB=3,BC=6,将矩形沿AC折叠,点D落在D'处,则重叠部分△AFC的面积是多少?
二、解答题
如图,在矩形ABCD中,E是边AB的中点,沿EC折叠矩形ABCD,使点B落在点P处,折痕为EC,连接AP并延长AP交CD于点F,连接BP.
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF//AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形.
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动.
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定点P、Q分别在边BA、BC上移动,求AE的长的取值范围
如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB'E;
(2)若AD=12,DC=18,求△AEF的面积.
如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,
(1)求BF长度;
(2)求CE的长度.
如图,长方形ABCD中,AB=4,BC=5,F为CD上一点,将长方形沿折痕AF折叠,点D恰好落在BC上的点E处,求△CFE的面积.
答案和解析
1.【答案】解:∵四边形ABCD为矩形,点B与点O重合,D点坐标为为(10,8),
∴DC=AB=8,AD=BC=10,
由折叠的性质可知,AF=AD=10,
设EF=DE=x,则EC=8?x,
由勾股定理得:BF2=102?82,
∴BF=6,
∴CF=10?6=4,
在Rt△EFC中,由勾股定理得:x2=42+(8?x)2,
解得:x=5,
EC=8?5=3,
∴E点的坐标为(10,3).
∴点F(6,0)和点?E(10,3).
2.【答案】(1)证明:由折叠可得,∠DEF=∠BEF,
∵AD//BC,
∴∠DEF=∠EFB,
∴∠BEF=∠EFB,
∴BE=BF;
(2)解:∵∠ABC=90°,
∴∠EBF=90°?18°=72°,
∴∠EBF=180°?∠BEF?∠EFB=72°
∴∠BFE=∠BEF=(180°?72°)÷2=54°;
(3)解:设AE=x,则BE=ED=8?x,
在Rt△ABE中AE2+AB2=BE2,即?x2+62=(8?x)2,
解得方程得x=74,
∴AE=74.
3.【答案】解:∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
根据题意得:Rt△ADE≌Rt△AFE,
∴∠AFE=90°,AF=10cm,EF=DE,
设EF=xcm,则DE=EF=xcm,CE=CD?CE=(8?x)cm,
在Rt△ABF中,由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC?BF=10?6=4(cm),
在Rt△ECF中,由勾股定理可得:EF2=CE2+CF2,
即x2=(8?x)2+42,
∴x=5
即:EF的长为5cm.
4.【答案】解:①设AE=x,则DE=AD?AE=9?x,
∵长方形沿EF折叠点B与D重合,
∴BE=DE,
在Rt△ABE中,AB2+AE2=BE2,
即32+x2=(9?x)2,
解得x=4,
故AE的长为4cm;
②由翻折的性质得,∠BEF=∠DEF,
∵矩形ABCD的对边AD//BC,
∴∠DEF=∠BFE,
∴∠BEF=∠BFE,
∴BF=BE=9?4=5cm,
∴CF=9?5=4cm,
过点F作FH⊥AD于H,则EH=DE?DH=5?4=1cm,
在Rt△EFH中,EF=EH2+HF2=10cm.
5.【答案】解:(1)由翻折的性质可知:∠2=∠BEF,
∵AD//BC,
∴∠2=∠1=55°,
∴∠3=180°?2×55°=70°.
(2)设DE=EB=x,
在Rt△ABE中,∵BE2=AB2+AE2,
∴x2=122+(18?x)2,
∴x=13,
∴AE=AD?DE=18?13=5,
∴S△ABE=12?AB?AE=12×12×5=30,
∵∠ABC=∠EBC',
∴∠ABE=∠FBC',
在△ABE和△C'BF中,
∠ABE=∠FBC'AB=BC'∠A=∠C'=90°,
∴△ABE≌△C'BF(ASA),
∴S△BFC'=S△ABE=30.
6.【答案】2
【解析】解:(1)∵四边形FDEG是正方形,
∴S△EFG=12×22=2.
故答案为:2.
(2)由折叠得∠GEF=∠DEF=α,
∵长方形的对边是平行的,
∴∠BFE=∠DEF=α,
∴∠EGB=∠BFE+∠DEF=2α,
∴∠FGD'=∠EGB=2α,
∴∠GFN=∠GFC'=180°?∠FGD'=180°?2α,
若∠GFE=13∠GFN时,
即α=13(180°?2α),
解得:α=36°.
(3)∠GPE=2∠GEP.
证明:由(2)可知:
∠FGD'=∠FGN=2α,
∵GP平分∠MGF,
∴∠PGF=α,
∴∠GPE=∠PGF+∠GFP=2α,
∴∠GPE=2∠GEP.
7.【答案】解:∵在正方形ABCD中,AD=AB=2,∠A=90°,
∴BD=22,
∵将此正方形的一只角DCE沿直线DE折叠,使C点恰好落在对角线BD上,
∴C'D=CD=2,∠DC'E=∠C=90°,CE=C'E=C'B=22?2,
∴BE=2(22?2)=4?22.
8.【答案】解:(1)过点G作GH⊥AD,则四边形ABGH为矩形,
∴GH=AB=8,AH=BG=10,由图形的折叠可知△BFG≌△EFG,
∴EG=BG=10,∠FEG=∠B=90°;
∴EH=6,AE=4,∠AEF+∠HEG=90°,
∵∠AEF+∠AFE=90°,
∴∠HEG=∠AFE,
又∵∠EHG=∠A=90°,
∴△EAF∽△GHE,
∴EFEG=AEGH,
∴EF=5,
∴S△EFG=12EF?EG=12×5×10=25.
(2)由图形的折叠可知四边形ABGF≌四边形HEGF,
∴BG=EG,AB=EH,∠BGF=∠EGF,
∵EF//BG,
∴∠BGF=∠EFG,
∴∠EGF=∠EFG,
∴EF=EG,
∴BG=EF,
∴四边形BGEF为平行四边形,
又∵EF=EG,
∴平行四边形BGEF为菱形;
连接BE,
BE,FG互相垂直平分,
在Rt△EFH中,
EF=BG=10,EH=AB=8,
由勾股定理可得FH=AF=6,
∴AE=AF+EF=16,
∴BE=AE2+AB2=85,
∴BO=45,
∴OG=BG2?BO2=25,
∵四边形BGEF是菱形,
∴FG=2OG=45,
答:折痕GF的长是45.
9.【答案】解:(1)∵四边形ABCD是矩形,
∴∠ABC=90°,AB=CD=4,AD=BC=5,
由折叠可知,AD=AF=5,DE=EF,
∴BF=AF2?AB2=52?42=3,
∴FC=BC?BF=5?3=2,
设EF=DE=x,则CE=4?x,
∵CF2+CE2=EF2,
∴22+(4?x)2=x2,
解得:x=52,
∴DE=52,
∴AE=AD2+DE2=52+(52)2=552;
(2)∵EC:FC=3:4,
∴设EC=3x,则FC=4x,
∴EF=CF2+CE2=5x,
∴DE=5x,
∴AB=CD=8x,
设AF=AD=y,则BF=y?4x,
在Rt△ABF中,AB2+BF2=AF2,
∴(8x)2+(y?4x)2=y2,
解得y=10x,
在Rt△ADE中,AD2+DE2=AE2,
∴(10x)2+(5x)2=(55)2,
解得x=1或x=?1(舍去),
∴AD=10,AB=8,
∴矩形ABCD的周长为(10+8)×2=36.
10.【答案】解:根据翻折的性质可知:AB=CD',∠AFB=∠CFD',∠B=∠D',
∴△CFD'≌△AFB,
∴BF=D'F,
设D'F=x,则FC=6?x,
在Rt△CFD'中,CF2=D'F2+CD'2,即为(6?x)2=x2+32,
解之得:x=94,
∴FC=BC?FB=6?94=154,
所以S△AFC=12?AB?FC=12×3×154=458.
11.【答案】解:(1)证明:在矩形ABCD中,AB//DC.
∵E为AB的中点,∴AE=BE.
由翻折可知:EC⊥BP,EP=BE=AE,
∴∠EAP=∠EPA,∠EPB=∠EBP.
在△ABP中,∠EAP+∠EPA+∠EPB+∠EBP=180°,
∴∠EPA+∠EPB=∠APB=90°,
∴EC//AF,∴四边形AECF为平行四边形.
(2)证明:∵△AEP是等边三角形,
∴AP=EP=AE,∠PAB=∠AEP=∠EPA=60°,∴∠PEC=∠BEC=60°.
由折叠的性质可得∠EPC=∠EBC=90°.
由(1)知∠APB=90°,∴∠APB=∠EPC.在△APB和△EPC中,
∵∠PAB=∠PEC,AP=EP,∠APB=∠EPC,∴△APB≌△EPC(ASA).
(3)∵AB=6,BC=4,E是边AB的中点,∴AE=BE=12AB=3.
在Rt△BEC中,EC=BE2+BC2=5.
∵四边形AECF为平行四边形,∴AF=EC=5.
如图,设CE与BP交于点H.
∵BE·BC=EC·BH,∴BH=125,∴PH=BH=125,∴BP=245.
在△BPA中,AP=AB2?BP2=185,∴PF=75.
过点C作CG⊥AF交其延长线于点G,∴CG=PH=125,
∴△CPF的面积S=12PF·CG=12×75×125=4225.
12.【答案】解:(1)证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EF//AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形;
(2)解:①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,
∴CE=BC=5cm,
在Rt△CDE中,DE=CE2?CD2=4cm,
在Rt△APE中,AE=1,AP=3?PB=3?PE,
∴EP2=12+(3?EP)2,
解得:EP=53cm,
∴菱形BFEP的边长为53cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴AE的长的取值范围是1cm≤AE≤3.
13.【答案】解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B'=90°,AD=CB=AB',
∵∠DAF+∠EAF=90°,∠B'AE+∠EAF=90°,
∴∠DAF=∠B'AE,
在△ADF和△AB'E中,
∠D=∠B'AD=AB'∠DAF=∠B'AE,
∴△ADF≌△AB'E(ASA).
(2)由折叠性质得FA=FC,
设FA=FC=x,则DF=DC?FC=18?x,
在Rt△ADF中,AD2+DF2=AF2,
∴122+(18?x)2=x2.
解得x=13.?
∵△ADF≌△AB'E(已证),
∴AE=AF=13,
∴S△AEF=12?AE?AD=12×12×13=78.
14.【答案】解:(1)设CE=xcm,EF=(8?x)cm,
在Rt△ABF中,BF=102?82=6cm,
(2)∵CF=10?6=4cm.
∴在Rt△ECF中,EF2=CE2+CF2,即(8?x)2=x2+42,
解得x=3.
故EC的长为3cm.
15.【答案】解:由折叠可知,AE=AD=5,
在Rt△ABE中,BE=AE2?AB23,
∴EC=BC?BE=2,
设CF=x,DF=4?x,由折叠的性质,EF=DF=4?x
在Rt△EFC中,CF2+CE2=EF2,即x2+22=(4?x)2,
解得,x=32,
∴△CFE的面积=12×CE×CF=32.
一、计算题
如图,长方形ABCD放在平面直角坐标系中,B点与原点重合.AB在y轴正半轴上已D点坐标为为(10,8).当AD沿一直线折叠时,顶点D落在BC边上的点F处(折痕为AE).请你求出点F和点E的坐标.
如图,长方形纸片ABCD,AD//BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF.
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
如图,已知长方形ABCD中,AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求EF的长.
如图,长方形ABCD中,折痕为EF,将此长方形沿EF折叠,使点B与D重合,已知AB=3cm,AD=9cm.
①求AE的长;
②求EF的长.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C'的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC'F的面积.
如图,一条宽为2(AB=2)的长方形纸带,E、F分别是边AD、BC上一点,∠DEF=α.将纸带沿EF折叠成图1,再沿GF折叠成图2.
(1)如图3,当点F与点C重合,且α=45°时,则S△EFG=______;
(2)如图2,若∠GFE=13∠GFN时,求α的值;
(3)在(2)下,作GP平分∠MGF交直线EF干于点P.如图4,若α<60°,试猜想∠GEP与∠GPE的数量关系,并证明你的结论.
如图,已知正方形ABCD边长为2,E是BC边上一点,将此正方形的一只角DCE沿直线DE折叠,使C点恰好落在对角线BD上,求BE的长.
如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10.
(1)当折痕的另一端F在AB边上时,如图.求△EFG的面积;
(2)当折痕的另一端F在AD边上时,如图.证明四边形BGEF为菱形,并求出折痕GF的长.
如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,AE是折痕.
(1)如图1,若AB=4,AD=5,求折痕AE的长;
(2)如图2,若AE=,且EC:FC=3:4,求矩形ABCD的周长.
如图,矩形ABCD中,AB=3,BC=6,将矩形沿AC折叠,点D落在D'处,则重叠部分△AFC的面积是多少?
二、解答题
如图,在矩形ABCD中,E是边AB的中点,沿EC折叠矩形ABCD,使点B落在点P处,折痕为EC,连接AP并延长AP交CD于点F,连接BP.
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF//AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形.
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动.
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定点P、Q分别在边BA、BC上移动,求AE的长的取值范围
如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB'E;
(2)若AD=12,DC=18,求△AEF的面积.
如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,
(1)求BF长度;
(2)求CE的长度.
如图,长方形ABCD中,AB=4,BC=5,F为CD上一点,将长方形沿折痕AF折叠,点D恰好落在BC上的点E处,求△CFE的面积.
答案和解析
1.【答案】解:∵四边形ABCD为矩形,点B与点O重合,D点坐标为为(10,8),
∴DC=AB=8,AD=BC=10,
由折叠的性质可知,AF=AD=10,
设EF=DE=x,则EC=8?x,
由勾股定理得:BF2=102?82,
∴BF=6,
∴CF=10?6=4,
在Rt△EFC中,由勾股定理得:x2=42+(8?x)2,
解得:x=5,
EC=8?5=3,
∴E点的坐标为(10,3).
∴点F(6,0)和点?E(10,3).
2.【答案】(1)证明:由折叠可得,∠DEF=∠BEF,
∵AD//BC,
∴∠DEF=∠EFB,
∴∠BEF=∠EFB,
∴BE=BF;
(2)解:∵∠ABC=90°,
∴∠EBF=90°?18°=72°,
∴∠EBF=180°?∠BEF?∠EFB=72°
∴∠BFE=∠BEF=(180°?72°)÷2=54°;
(3)解:设AE=x,则BE=ED=8?x,
在Rt△ABE中AE2+AB2=BE2,即?x2+62=(8?x)2,
解得方程得x=74,
∴AE=74.
3.【答案】解:∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
根据题意得:Rt△ADE≌Rt△AFE,
∴∠AFE=90°,AF=10cm,EF=DE,
设EF=xcm,则DE=EF=xcm,CE=CD?CE=(8?x)cm,
在Rt△ABF中,由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC?BF=10?6=4(cm),
在Rt△ECF中,由勾股定理可得:EF2=CE2+CF2,
即x2=(8?x)2+42,
∴x=5
即:EF的长为5cm.
4.【答案】解:①设AE=x,则DE=AD?AE=9?x,
∵长方形沿EF折叠点B与D重合,
∴BE=DE,
在Rt△ABE中,AB2+AE2=BE2,
即32+x2=(9?x)2,
解得x=4,
故AE的长为4cm;
②由翻折的性质得,∠BEF=∠DEF,
∵矩形ABCD的对边AD//BC,
∴∠DEF=∠BFE,
∴∠BEF=∠BFE,
∴BF=BE=9?4=5cm,
∴CF=9?5=4cm,
过点F作FH⊥AD于H,则EH=DE?DH=5?4=1cm,
在Rt△EFH中,EF=EH2+HF2=10cm.
5.【答案】解:(1)由翻折的性质可知:∠2=∠BEF,
∵AD//BC,
∴∠2=∠1=55°,
∴∠3=180°?2×55°=70°.
(2)设DE=EB=x,
在Rt△ABE中,∵BE2=AB2+AE2,
∴x2=122+(18?x)2,
∴x=13,
∴AE=AD?DE=18?13=5,
∴S△ABE=12?AB?AE=12×12×5=30,
∵∠ABC=∠EBC',
∴∠ABE=∠FBC',
在△ABE和△C'BF中,
∠ABE=∠FBC'AB=BC'∠A=∠C'=90°,
∴△ABE≌△C'BF(ASA),
∴S△BFC'=S△ABE=30.
6.【答案】2
【解析】解:(1)∵四边形FDEG是正方形,
∴S△EFG=12×22=2.
故答案为:2.
(2)由折叠得∠GEF=∠DEF=α,
∵长方形的对边是平行的,
∴∠BFE=∠DEF=α,
∴∠EGB=∠BFE+∠DEF=2α,
∴∠FGD'=∠EGB=2α,
∴∠GFN=∠GFC'=180°?∠FGD'=180°?2α,
若∠GFE=13∠GFN时,
即α=13(180°?2α),
解得:α=36°.
(3)∠GPE=2∠GEP.
证明:由(2)可知:
∠FGD'=∠FGN=2α,
∵GP平分∠MGF,
∴∠PGF=α,
∴∠GPE=∠PGF+∠GFP=2α,
∴∠GPE=2∠GEP.
7.【答案】解:∵在正方形ABCD中,AD=AB=2,∠A=90°,
∴BD=22,
∵将此正方形的一只角DCE沿直线DE折叠,使C点恰好落在对角线BD上,
∴C'D=CD=2,∠DC'E=∠C=90°,CE=C'E=C'B=22?2,
∴BE=2(22?2)=4?22.
8.【答案】解:(1)过点G作GH⊥AD,则四边形ABGH为矩形,
∴GH=AB=8,AH=BG=10,由图形的折叠可知△BFG≌△EFG,
∴EG=BG=10,∠FEG=∠B=90°;
∴EH=6,AE=4,∠AEF+∠HEG=90°,
∵∠AEF+∠AFE=90°,
∴∠HEG=∠AFE,
又∵∠EHG=∠A=90°,
∴△EAF∽△GHE,
∴EFEG=AEGH,
∴EF=5,
∴S△EFG=12EF?EG=12×5×10=25.
(2)由图形的折叠可知四边形ABGF≌四边形HEGF,
∴BG=EG,AB=EH,∠BGF=∠EGF,
∵EF//BG,
∴∠BGF=∠EFG,
∴∠EGF=∠EFG,
∴EF=EG,
∴BG=EF,
∴四边形BGEF为平行四边形,
又∵EF=EG,
∴平行四边形BGEF为菱形;
连接BE,
BE,FG互相垂直平分,
在Rt△EFH中,
EF=BG=10,EH=AB=8,
由勾股定理可得FH=AF=6,
∴AE=AF+EF=16,
∴BE=AE2+AB2=85,
∴BO=45,
∴OG=BG2?BO2=25,
∵四边形BGEF是菱形,
∴FG=2OG=45,
答:折痕GF的长是45.
9.【答案】解:(1)∵四边形ABCD是矩形,
∴∠ABC=90°,AB=CD=4,AD=BC=5,
由折叠可知,AD=AF=5,DE=EF,
∴BF=AF2?AB2=52?42=3,
∴FC=BC?BF=5?3=2,
设EF=DE=x,则CE=4?x,
∵CF2+CE2=EF2,
∴22+(4?x)2=x2,
解得:x=52,
∴DE=52,
∴AE=AD2+DE2=52+(52)2=552;
(2)∵EC:FC=3:4,
∴设EC=3x,则FC=4x,
∴EF=CF2+CE2=5x,
∴DE=5x,
∴AB=CD=8x,
设AF=AD=y,则BF=y?4x,
在Rt△ABF中,AB2+BF2=AF2,
∴(8x)2+(y?4x)2=y2,
解得y=10x,
在Rt△ADE中,AD2+DE2=AE2,
∴(10x)2+(5x)2=(55)2,
解得x=1或x=?1(舍去),
∴AD=10,AB=8,
∴矩形ABCD的周长为(10+8)×2=36.
10.【答案】解:根据翻折的性质可知:AB=CD',∠AFB=∠CFD',∠B=∠D',
∴△CFD'≌△AFB,
∴BF=D'F,
设D'F=x,则FC=6?x,
在Rt△CFD'中,CF2=D'F2+CD'2,即为(6?x)2=x2+32,
解之得:x=94,
∴FC=BC?FB=6?94=154,
所以S△AFC=12?AB?FC=12×3×154=458.
11.【答案】解:(1)证明:在矩形ABCD中,AB//DC.
∵E为AB的中点,∴AE=BE.
由翻折可知:EC⊥BP,EP=BE=AE,
∴∠EAP=∠EPA,∠EPB=∠EBP.
在△ABP中,∠EAP+∠EPA+∠EPB+∠EBP=180°,
∴∠EPA+∠EPB=∠APB=90°,
∴EC//AF,∴四边形AECF为平行四边形.
(2)证明:∵△AEP是等边三角形,
∴AP=EP=AE,∠PAB=∠AEP=∠EPA=60°,∴∠PEC=∠BEC=60°.
由折叠的性质可得∠EPC=∠EBC=90°.
由(1)知∠APB=90°,∴∠APB=∠EPC.在△APB和△EPC中,
∵∠PAB=∠PEC,AP=EP,∠APB=∠EPC,∴△APB≌△EPC(ASA).
(3)∵AB=6,BC=4,E是边AB的中点,∴AE=BE=12AB=3.
在Rt△BEC中,EC=BE2+BC2=5.
∵四边形AECF为平行四边形,∴AF=EC=5.
如图,设CE与BP交于点H.
∵BE·BC=EC·BH,∴BH=125,∴PH=BH=125,∴BP=245.
在△BPA中,AP=AB2?BP2=185,∴PF=75.
过点C作CG⊥AF交其延长线于点G,∴CG=PH=125,
∴△CPF的面积S=12PF·CG=12×75×125=4225.
12.【答案】解:(1)证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EF//AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形;
(2)解:①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,
∴CE=BC=5cm,
在Rt△CDE中,DE=CE2?CD2=4cm,
在Rt△APE中,AE=1,AP=3?PB=3?PE,
∴EP2=12+(3?EP)2,
解得:EP=53cm,
∴菱形BFEP的边长为53cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴AE的长的取值范围是1cm≤AE≤3.
13.【答案】解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B'=90°,AD=CB=AB',
∵∠DAF+∠EAF=90°,∠B'AE+∠EAF=90°,
∴∠DAF=∠B'AE,
在△ADF和△AB'E中,
∠D=∠B'AD=AB'∠DAF=∠B'AE,
∴△ADF≌△AB'E(ASA).
(2)由折叠性质得FA=FC,
设FA=FC=x,则DF=DC?FC=18?x,
在Rt△ADF中,AD2+DF2=AF2,
∴122+(18?x)2=x2.
解得x=13.?
∵△ADF≌△AB'E(已证),
∴AE=AF=13,
∴S△AEF=12?AE?AD=12×12×13=78.
14.【答案】解:(1)设CE=xcm,EF=(8?x)cm,
在Rt△ABF中,BF=102?82=6cm,
(2)∵CF=10?6=4cm.
∴在Rt△ECF中,EF2=CE2+CF2,即(8?x)2=x2+42,
解得x=3.
故EC的长为3cm.
15.【答案】解:由折叠可知,AE=AD=5,
在Rt△ABE中,BE=AE2?AB23,
∴EC=BC?BE=2,
设CF=x,DF=4?x,由折叠的性质,EF=DF=4?x
在Rt△EFC中,CF2+CE2=EF2,即x2+22=(4?x)2,
解得,x=32,
∴△CFE的面积=12×CE×CF=32.
