2021-2022学年沪科版数学九年级上册第23章 解直角三角形单元测试自我综合评价 (word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级上册第23章 解直角三角形单元测试自我综合评价 (word版含答案) | 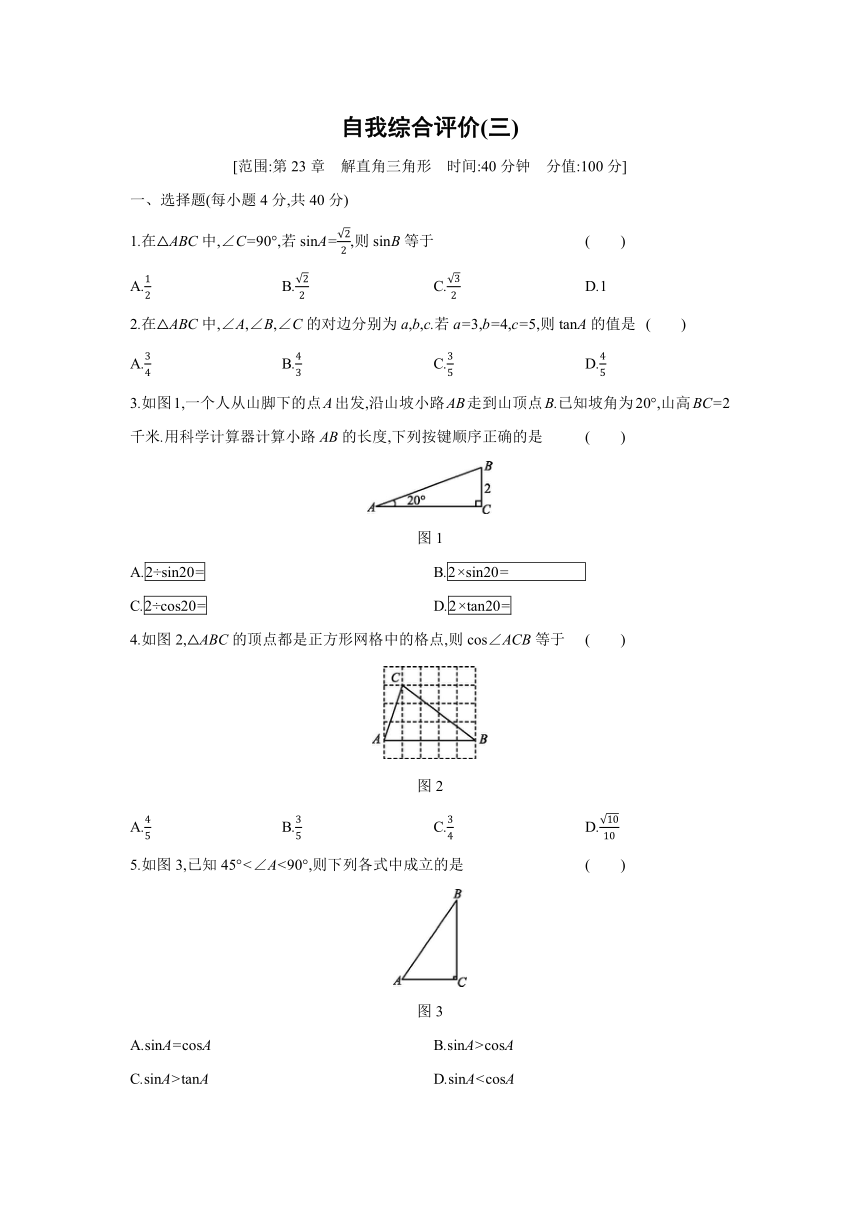 | |
| 格式 | docx | ||
| 文件大小 | 205.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 10:58:25 | ||
图片预览



文档简介
自我综合评价(三)
[范围:第23章 解直角三角形 时间:40分钟 分值:100分]
一、选择题(每小题4分,共40分)
1.在△ABC中,∠C=90°,若sinA=22,则sinB等于 ( )
A.12 B.22 C.32 D.1
2.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c.若a=3,b=4,c=5,则tanA的值是 ( )
A.34 B.43 C.35 D.45
3.如图1,一个人从山脚下的点A出发,沿山坡小路AB走到山顶点B.已知坡角为20°,山高BC=2千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是 ( )
图1
A.2÷sin20= B.2×sin20=
C.2÷cos20= D.2×tan20=
4.如图2,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于 ( )
图2
A.45 B.35 C.34 D.1010
5.如图3,已知45°<∠A<90°,则下列各式中成立的是 ( )
图3
A.sinA=cosA B.sinA>cosA
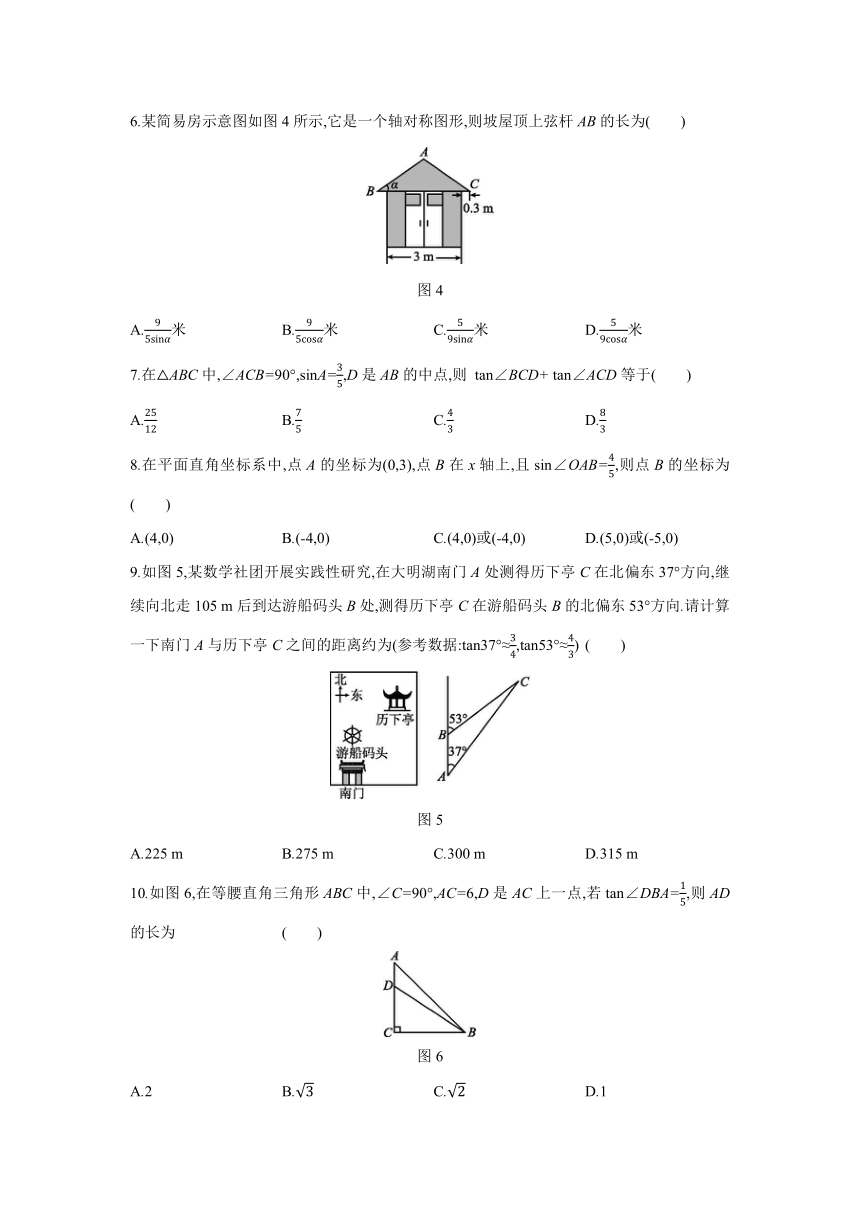
C.sinA>tanA D.sinA 6.某简易房示意图如图4所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )
图4
A.95sinα米 B.95cosα米 C.59sinα米 D.59cosα米
7.在△ABC中,∠ACB=90°,sinA=35,D是AB的中点,则 tan∠BCD+ tan∠ACD等于( )
A.2512 B.75 C.43 D.83
8.在平面直角坐标系中,点A的坐标为(0,3),点B在x轴上,且sin∠OAB=45,则点B的坐标为( )
A.(4,0) B.(-4,0) C.(4,0)或(-4,0) D.(5,0)或(-5,0)
9.如图5,某数学社团开展实践性研究,在大明湖南门A处测得历下亭C在北偏东37°方向,继续向北走105 m后到达游船码头B处,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为(参考数据:tan37°≈34,tan53°≈43) ( )
图5
A.225 m B.275 m C.300 m D.315 m
10.如图6,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=15,则AD的长为 ( )
图6
A.2 B.3 C.2 D.1
二、填空题(每小题5分,共20分)
11.在Rt△ABC中,∠C=90°,sinA=513,则cosB= .?
12.如图7,在△ABC中,AB=BC,以点A为圆心,AC长为半径画弧,交BC于点C和点D,再分别以点C,D为圆心,大于12CD长为半径画弧,两弧相交于点E,作射线AE交BC于点M,若CM=1,BD=3,则cosB= .?
图7
13.如图8,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距离旗杆底部点B6 m的位置,在点D处测得旗杆顶端点A的仰角为53°,若测角仪的高度是1.5 m,则旗杆AB的高度约为 m.(精确到0.1 m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)?
图8
14.在△ABC中,AB=45,AC=25,tanB=12,则BC的长为 .?
三、解答题(共40分)
15.(6分)计算:sin245°+3tan30°tan60°-2cos60°.
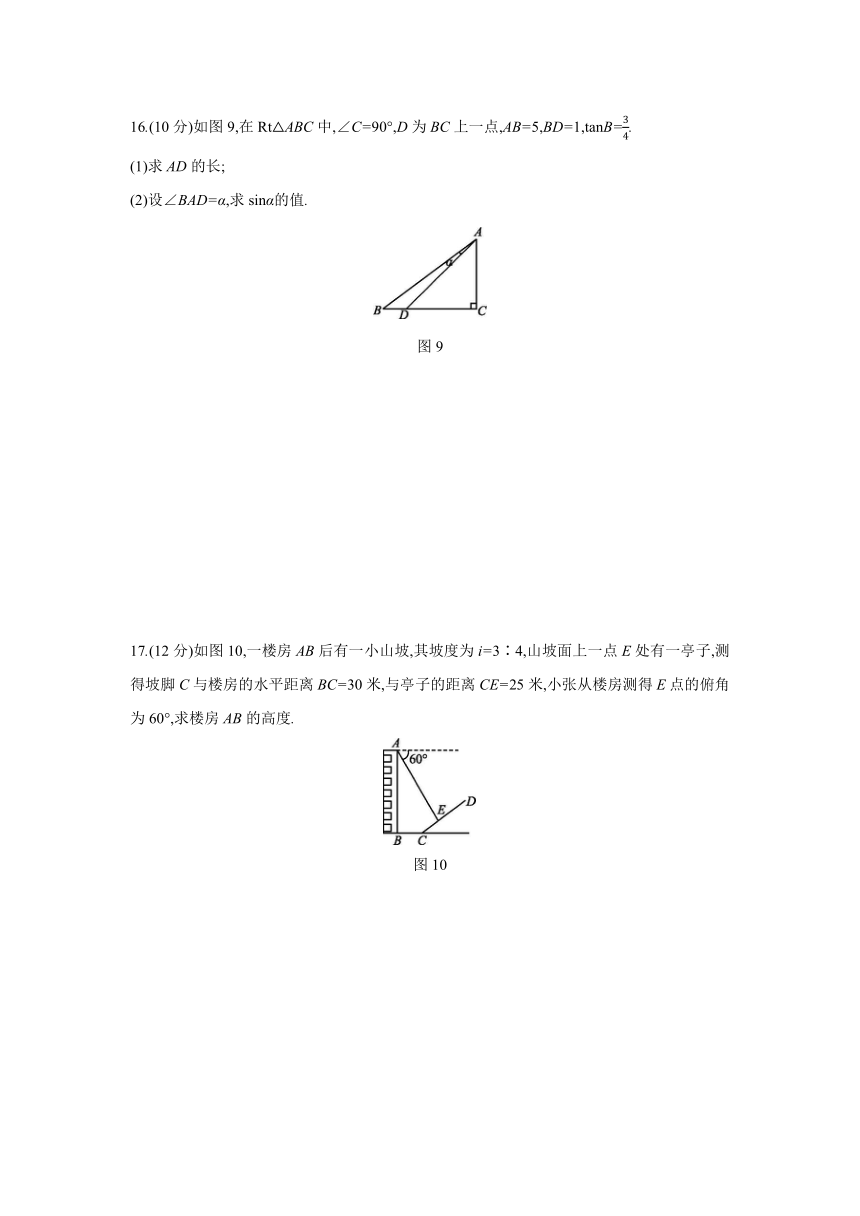
16.(10分)如图9,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tanB=34.
(1)求AD的长;
(2)设∠BAD=α,求sinα的值.
图9
17.(12分)如图10,一楼房AB后有一小山坡,其坡度为i=3∶4,山坡面上一点E处有一亭子,测得坡脚C与楼房的水平距离BC=30米,与亭子的距离CE=25米,小张从楼房测得E点的俯角为60°,求楼房AB的高度.
图10
18.(12分)如图11,台风中心位于点O处,并沿北偏东45°方向(OC方向)以40千米/时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离602千米的地方有一城市A.
(1)A市是否会受到此台风的影响?为什么?
(2)在点O的北偏东15°方向上,距离80千米的地方还有一城市B,则B市是否会受到此台风的影响?若受到影响,请求出受到影响的时间;若不受影响,请说明理由.
图11
教师详解详析
1.B
2.A
3.A
4.D [解析] ∵AB=5,BC=32+42=5,AC=32+12=10,
∴BA=BC,
∴∠ACB=∠CAB,
∴cos∠ACB=cos∠CAB=110=1010.
故选D.
5.B [解析] 根据锐角的正弦值随角度的增大而增大,余弦值随角度的增大而减小判断.也可用特殊值检验.
6.B [解析] 如图,过点A作AD⊥BC于点D,则BD=32+0.3=95.∵cosα=BDAB,∴cosα=95AB,解得AB=95cosα米.故选B.
7.A [解析] 如图,由sinA=35,设BC=3k,AB=5k.由勾股定理,得AC=4k.根据直角三角形斜边上的中线等于斜边的一半,得CD=AD=BD,∴∠BCD=∠B,∠ACD=∠A,故tan∠BCD+tan∠ACD=43+34=2512.
8.C [解析] ①如图,当点B在x轴的正半轴上时.
∵sin∠OAB=45,
∴设OB=4x,AB=5x,
∴由勾股定理,得32+(4x)2=(5x)2,
解得x=1,
∴OB=4,则点B的坐标是(4,0);
②同理,当点B在x轴的负半轴上时,点B的坐标是(-4,0).
故点B的坐标是(4,0)或(-4,0).
9.C [解析] 如图,过点C作CE⊥AB交AB的延长线于点E.
设EC=x m,BE=y m.
在Rt△ECB中,tan53°=ECEB,即xy=43.
在Rt△AEC中,tan37°=ECAE,即x105+y=34,解得x=180,y=135,∴AC=EC2+AE2=1802+2402=300(m).故选C.
10.A [解析] 如图,过点D作DE⊥AB,垂足为E.易证△ADE为等腰直角三角形,AE=DE.在Rt△BDE中,tan∠DBA=DEBE=AEBE=15,所以BE=5AE.在等腰直角三角形ABC中,∠C=90°,AC=6,由勾股定理可求出AB=62,所以AE=2.在等腰直角三角形ADE中,利用勾股定理可求出AD的长为2.故选A.
11.513 [解析] 方法1:由互余两角三角函数关系可知cosB=sinA=513;
方法2:可设BC=5k,AB=13k,
∴cosB=BCAB=5k13k=513.
12.45 [解析] 由作图可知,AM⊥DC,DM=MC=1.
∵BD=3,
∴BM=3+1=4,AB=BC=3+2=5,
∴cosB=BMAB=45.故答案为45.
13.9.5 [解析] 如图,过点D作DE⊥AB于点E.
∵在点D处测得旗杆顶端点A的仰角为53°,
∴∠ADE=53°.
∵BC=DE=6 m,
∴AE=DE·tan53°≈6×1.33=7.98(m),
∴AB=AE+BE=AE+CD≈7.98+1.5=9.48(m)≈9.5(m).
14.10或6 [解析] 当∠ACB为锐角时,如图所示,
过点A作AD⊥BC于点D.
在Rt△ABD中,tanB=ADBD=12,
设AD=x,则BD=2x,则AB=x2+(2x)2=5x=45,解得x=4,
故AD=4,BD=8.
在Rt△ACD中,CD=AC2-AD2=20-16=2,
故BC=BD+CD=8+2=10;
当∠ACB为钝角时,
同理可得BC=BD-CD=8-2=6.
故答案为10或6.
15.解:原式=(22)2+3×33×3-2×12=12+3-1=212.
16.解:(1)∵tanB=34,可设AC=3x,得BC=4x.
由勾股定理,得(3x)2+(4x)2=52,
解得x1=-1(舍去),x2=1,
∴AC=3,BC=4.
∵BD=1,
∴CD=3,
∴AD=CD2+AC2=32.
(2)过点D作DE⊥AB于点E.
∵tanB=34,可设DE=3y,则BE=4y.
由勾股定理,得(3y)2+(4y)2=12,
解得y1=-15(舍去),y2=15,
∴DE=35,
∴sinα=DEAD=210.
17.解:如图,过点E作EF⊥BC的延长线于点F,作EH⊥AB于点H.
在Rt△CEF中,
∵i=EF∶CF=3∶4,CE=25米,
∴EF=15米,CF=20米,
∴BH=EF=15米,
HE=BF=BC+CF=50(米).
在Rt△AHE中,∵∠HAE=30°,
∴AH=HEtan30°=503(米),
∴AB=AH+HB=(503+15)米.
答:楼房AB的高度为(503+15)米.
18.解:(1)不会.理由:如图,过点A作AE⊥OC于点E.在Rt△AOE中,sin45°=AEOA,
∴AE=602×22=60(千米).
∵60千米>50千米,
∴A市不会受到此台风的影响.
(2)会.如图,过点B作BF⊥OC于点F.
在Rt△BOF中,
∵∠BOF=45°-15°=30°,sin30°=BFOB,
∴BF=80×12=40(千米).
∵40千米<50千米,
∴B市会受到台风的影响.
如图,以点B为圆心,50千米为半径作圆交OC于点G,H.
在Rt△BGF中,∵BF=40千米,
∴GF=502-402=30(千米).
同理,FH=30千米.
∴GH=60千米,则60÷40=1.5(时),
∴B市受到台风影响的时间为1.5小时.
[范围:第23章 解直角三角形 时间:40分钟 分值:100分]
一、选择题(每小题4分,共40分)
1.在△ABC中,∠C=90°,若sinA=22,则sinB等于 ( )
A.12 B.22 C.32 D.1
2.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c.若a=3,b=4,c=5,则tanA的值是 ( )
A.34 B.43 C.35 D.45
3.如图1,一个人从山脚下的点A出发,沿山坡小路AB走到山顶点B.已知坡角为20°,山高BC=2千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是 ( )
图1
A.2÷sin20= B.2×sin20=
C.2÷cos20= D.2×tan20=
4.如图2,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于 ( )
图2
A.45 B.35 C.34 D.1010
5.如图3,已知45°<∠A<90°,则下列各式中成立的是 ( )
图3
A.sinA=cosA B.sinA>cosA
C.sinA>tanA D.sinA
图4
A.95sinα米 B.95cosα米 C.59sinα米 D.59cosα米
7.在△ABC中,∠ACB=90°,sinA=35,D是AB的中点,则 tan∠BCD+ tan∠ACD等于( )
A.2512 B.75 C.43 D.83
8.在平面直角坐标系中,点A的坐标为(0,3),点B在x轴上,且sin∠OAB=45,则点B的坐标为( )
A.(4,0) B.(-4,0) C.(4,0)或(-4,0) D.(5,0)或(-5,0)
9.如图5,某数学社团开展实践性研究,在大明湖南门A处测得历下亭C在北偏东37°方向,继续向北走105 m后到达游船码头B处,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为(参考数据:tan37°≈34,tan53°≈43) ( )
图5
A.225 m B.275 m C.300 m D.315 m
10.如图6,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=15,则AD的长为 ( )
图6
A.2 B.3 C.2 D.1
二、填空题(每小题5分,共20分)
11.在Rt△ABC中,∠C=90°,sinA=513,则cosB= .?
12.如图7,在△ABC中,AB=BC,以点A为圆心,AC长为半径画弧,交BC于点C和点D,再分别以点C,D为圆心,大于12CD长为半径画弧,两弧相交于点E,作射线AE交BC于点M,若CM=1,BD=3,则cosB= .?
图7
13.如图8,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距离旗杆底部点B6 m的位置,在点D处测得旗杆顶端点A的仰角为53°,若测角仪的高度是1.5 m,则旗杆AB的高度约为 m.(精确到0.1 m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)?
图8
14.在△ABC中,AB=45,AC=25,tanB=12,则BC的长为 .?
三、解答题(共40分)
15.(6分)计算:sin245°+3tan30°tan60°-2cos60°.
16.(10分)如图9,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tanB=34.
(1)求AD的长;
(2)设∠BAD=α,求sinα的值.
图9
17.(12分)如图10,一楼房AB后有一小山坡,其坡度为i=3∶4,山坡面上一点E处有一亭子,测得坡脚C与楼房的水平距离BC=30米,与亭子的距离CE=25米,小张从楼房测得E点的俯角为60°,求楼房AB的高度.
图10
18.(12分)如图11,台风中心位于点O处,并沿北偏东45°方向(OC方向)以40千米/时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离602千米的地方有一城市A.
(1)A市是否会受到此台风的影响?为什么?
(2)在点O的北偏东15°方向上,距离80千米的地方还有一城市B,则B市是否会受到此台风的影响?若受到影响,请求出受到影响的时间;若不受影响,请说明理由.
图11
教师详解详析
1.B
2.A
3.A
4.D [解析] ∵AB=5,BC=32+42=5,AC=32+12=10,
∴BA=BC,
∴∠ACB=∠CAB,
∴cos∠ACB=cos∠CAB=110=1010.
故选D.
5.B [解析] 根据锐角的正弦值随角度的增大而增大,余弦值随角度的增大而减小判断.也可用特殊值检验.
6.B [解析] 如图,过点A作AD⊥BC于点D,则BD=32+0.3=95.∵cosα=BDAB,∴cosα=95AB,解得AB=95cosα米.故选B.
7.A [解析] 如图,由sinA=35,设BC=3k,AB=5k.由勾股定理,得AC=4k.根据直角三角形斜边上的中线等于斜边的一半,得CD=AD=BD,∴∠BCD=∠B,∠ACD=∠A,故tan∠BCD+tan∠ACD=43+34=2512.
8.C [解析] ①如图,当点B在x轴的正半轴上时.
∵sin∠OAB=45,
∴设OB=4x,AB=5x,
∴由勾股定理,得32+(4x)2=(5x)2,
解得x=1,
∴OB=4,则点B的坐标是(4,0);
②同理,当点B在x轴的负半轴上时,点B的坐标是(-4,0).
故点B的坐标是(4,0)或(-4,0).
9.C [解析] 如图,过点C作CE⊥AB交AB的延长线于点E.
设EC=x m,BE=y m.
在Rt△ECB中,tan53°=ECEB,即xy=43.
在Rt△AEC中,tan37°=ECAE,即x105+y=34,解得x=180,y=135,∴AC=EC2+AE2=1802+2402=300(m).故选C.
10.A [解析] 如图,过点D作DE⊥AB,垂足为E.易证△ADE为等腰直角三角形,AE=DE.在Rt△BDE中,tan∠DBA=DEBE=AEBE=15,所以BE=5AE.在等腰直角三角形ABC中,∠C=90°,AC=6,由勾股定理可求出AB=62,所以AE=2.在等腰直角三角形ADE中,利用勾股定理可求出AD的长为2.故选A.
11.513 [解析] 方法1:由互余两角三角函数关系可知cosB=sinA=513;
方法2:可设BC=5k,AB=13k,
∴cosB=BCAB=5k13k=513.
12.45 [解析] 由作图可知,AM⊥DC,DM=MC=1.
∵BD=3,
∴BM=3+1=4,AB=BC=3+2=5,
∴cosB=BMAB=45.故答案为45.
13.9.5 [解析] 如图,过点D作DE⊥AB于点E.
∵在点D处测得旗杆顶端点A的仰角为53°,
∴∠ADE=53°.
∵BC=DE=6 m,
∴AE=DE·tan53°≈6×1.33=7.98(m),
∴AB=AE+BE=AE+CD≈7.98+1.5=9.48(m)≈9.5(m).
14.10或6 [解析] 当∠ACB为锐角时,如图所示,
过点A作AD⊥BC于点D.
在Rt△ABD中,tanB=ADBD=12,
设AD=x,则BD=2x,则AB=x2+(2x)2=5x=45,解得x=4,
故AD=4,BD=8.
在Rt△ACD中,CD=AC2-AD2=20-16=2,
故BC=BD+CD=8+2=10;
当∠ACB为钝角时,
同理可得BC=BD-CD=8-2=6.
故答案为10或6.
15.解:原式=(22)2+3×33×3-2×12=12+3-1=212.
16.解:(1)∵tanB=34,可设AC=3x,得BC=4x.
由勾股定理,得(3x)2+(4x)2=52,
解得x1=-1(舍去),x2=1,
∴AC=3,BC=4.
∵BD=1,
∴CD=3,
∴AD=CD2+AC2=32.
(2)过点D作DE⊥AB于点E.
∵tanB=34,可设DE=3y,则BE=4y.
由勾股定理,得(3y)2+(4y)2=12,
解得y1=-15(舍去),y2=15,
∴DE=35,
∴sinα=DEAD=210.
17.解:如图,过点E作EF⊥BC的延长线于点F,作EH⊥AB于点H.
在Rt△CEF中,
∵i=EF∶CF=3∶4,CE=25米,
∴EF=15米,CF=20米,
∴BH=EF=15米,
HE=BF=BC+CF=50(米).
在Rt△AHE中,∵∠HAE=30°,
∴AH=HEtan30°=503(米),
∴AB=AH+HB=(503+15)米.
答:楼房AB的高度为(503+15)米.
18.解:(1)不会.理由:如图,过点A作AE⊥OC于点E.在Rt△AOE中,sin45°=AEOA,
∴AE=602×22=60(千米).
∵60千米>50千米,
∴A市不会受到此台风的影响.
(2)会.如图,过点B作BF⊥OC于点F.
在Rt△BOF中,
∵∠BOF=45°-15°=30°,sin30°=BFOB,
∴BF=80×12=40(千米).
∵40千米<50千米,
∴B市会受到台风的影响.
如图,以点B为圆心,50千米为半径作圆交OC于点G,H.
在Rt△BGF中,∵BF=40千米,
∴GF=502-402=30(千米).
同理,FH=30千米.
∴GH=60千米,则60÷40=1.5(时),
∴B市受到台风影响的时间为1.5小时.
