2021-2022学年苏科新版七年级上册数学《第3章 代数式》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年苏科新版七年级上册数学《第3章 代数式》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 217.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 20:30:32 | ||
图片预览




文档简介
2021-2022学年苏科新版七年级上册数学《第3章
代数式》单元测试卷
一.选择题
1.下列说法正确的是( )
A.2a是代数式,1不是代数式
B.代数式表示3﹣b除a
C.当x=4时,代数式的值为0
D.零是最小的整数
2.下列式子,符合代数式书写格式的是( )
A.a+b人
B.1a
C.a×8
D.
3.一个长方形的周长为30cm,若它的一边长用字母a(cm)表示,则它的面积是( )
A.a(15﹣a)cm2
B.a(30﹣a)cm2
C.a(30﹣2a)cm2
D.a(15+a)cm2
4.如图,梯形上、下底分别为a,b,高线长恰好等于圆的直径2r,则图中阴影部分的面积是( )
A.(a+b)r﹣πr2
B.abr﹣πr2
C.2(a+b)r﹣πr2
D.2abr﹣πr2
5.下列代数式中整式有( )
,2x+y,
a2b,,,0.5,a.
A.4个
B.5个
C.6个
D.7个
6.整式2a+b,,﹣7,﹣
a2bc,中,单项式的个数是( )
A.2
B.3
C.4
D.5
7.下列式子,符合书写格式的是( )
A.a÷c
B.1x
C.a?a?a
D.
8.下列说法正确的是( )
A.﹣xy一定是负数
B.m2﹣2m+3是二次三项式
C.﹣5不是单项式
D.的系数是
9.观察下列图形中点的个数,若按其规律再画下去,可以得到第5个图形中所有点的个数为( )
A.16个
B.25个
C.36个
D.49个
10.如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列:a1=1,a2=2.a3=3,a4=3,a5=6,a6=4,a7=10,a8=5…,则a99+a100的值为( )
A.1275
B.1326
C.1378
D.1431
二.填空题
11.若练习本每本a元,铅笔每支b元,那么代数式8a+3b表示的意义是
.
12.一个跳蚤在一条数轴上从原点开始,第一次向右跳1个单位长度,紧接着第二次向左跳2个单位长度,第三次向右跳3个单位长度,第四次向左跳4个单位长度…以此规律跳下去,当它跳第100次落下时,落点处距离原点
个单位长度.
13.请写出一个只含有字母x,y,且次数不超过2的整式:
.
14.代数式6a2的实际意义:
.
15.如果x表示一辆火车行驶的速度,那么1.5x可以解释为
.
16.一个两位数,十位上的数字是2,个位上的数字是x,这个两位数是
.
17.如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式是
.
18.若多项式(m+4)x3+xn﹣1﹣5x﹣6是关于x的二次三项式,则m+n﹣(x﹣2)2的最大值为
.
19.甲数x的5倍与乙数y的的差可以表示为:
.
20.单项式﹣5t的系数是
.
三.解答题
21.滴滴公布了新的滴滴快车计价规则,车费由“总里程费+总时长费”两部分构成,不同时段收费标准不同,具体收费标准如下表,如果车费不足起步价,则按起步价收费.
时间段
里程费(元/千米)
时长费(元/分钟)
起步价(元)
06:00﹣10:00
1.80
0.80
14.00
10:00﹣17:00
1.45
0.40
13.00
17:00﹣21:00
1.50
0.80
14.00
21:00﹣6:00
0.80
0.80
14.00
(1)小明早上7:10乘坐滴滴快车上学,行车里程6千米,行车时间10分钟,则应付车费多少元?
(2)小云17:10放学回家,行车里程2千米,行车时间12分钟,则应付车费多少元?
(3)下晚自习后小明乘坐滴滴快车回家,20:45在学校上车,由于堵车,平均速度是a千米/小时,15分钟后走另外一条路回家,平均速度是b千米/小时,10分钟后到家,则他应付车费多少元?
22.请将下列代数式进行分类(至少三种以上)
,a,3x,,,,a2+x,4x2ay,x+8.
23.请你结合自身生活实际,设计具体情境,解释下列代数式的意义:
①(1﹣20%)x;
②a3;
③;
④.
24.已知如图,在数轴上点A,B所对应的数是﹣4,4.
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于﹣4,则称代数式N,是线段AB的吉祥式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的吉祥式.
问题:
(1)关于x代数式|x﹣1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值是
,取得的最小值是
;所以代数式|x﹣1|
(填是或不是)线段AB的吉祥式.
(2)以下关于x的代数式:
①x2+1;②|x+2|﹣|x﹣1|﹣1,是线段AB的封闭代数式是
.(填序号)
(3)关于x的代数式|x+1|+2a是线段AB的吉祥式,请求出有理数a的最大值和最小值.
25.方方和圆圆的房间窗帘的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径都分别相同),它们的窗户能射进阳光的面积分别是多少(窗框面积不计)谁的窗户射进阳光的面积大?
26.观察下列算式:
①1×3﹣22=3﹣4=﹣1 ②2×4﹣32=8﹣9=﹣1 ③3×5﹣42=15﹣16=﹣1
(1)请你按照三个算式的规律写出第④个、第⑤个算式;
(2)把这个规律用含字母的式子表示出来,并说明其正确性.
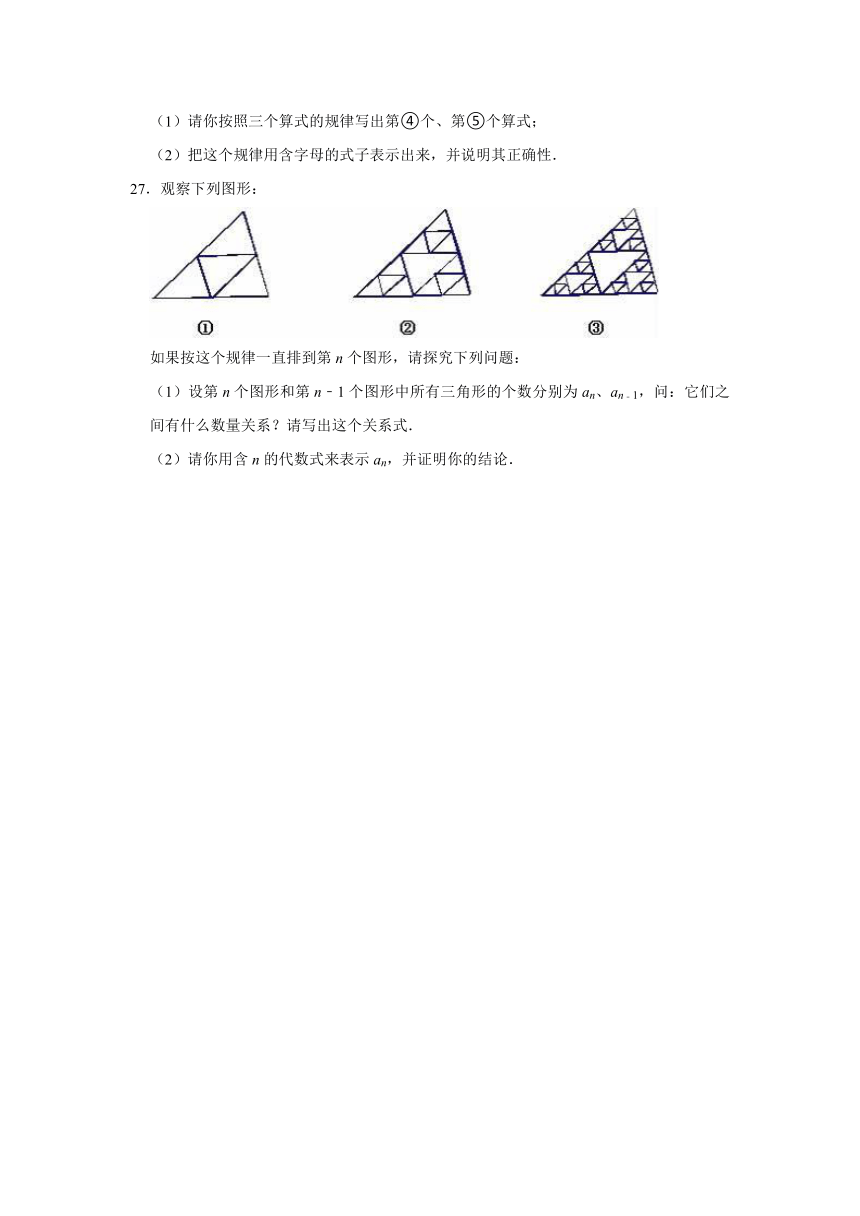
27.观察下列图形:
如果按这个规律一直排到第n个图形,请探究下列问题:
(1)设第n个图形和第n﹣1个图形中所有三角形的个数分别为an、an﹣1,问:它们之间有什么数量关系?请写出这个关系式.
(2)请你用含n的代数式来表示an,并证明你的结论.
参考答案与试题解析
一.选择题
1.解:单独的数或字母都是代数式,故A不正确;
代数式表示3﹣b除以a或3﹣b与a的商,故B不正确;
C正确;
整数包括正整数、0、负整数,故D不正确.
故选:C.
2.解:A、a+b人的正确书写格式是(a+b)人,故本选项错误;
B、1a的正确书写格式是a,故本选项错误;
C、a×8的正确书写形式是8a,故本选项错误;
D、符合代数式的书写要求,故本选项正确;
故选:D.
3.解:另一边长=×30﹣a=15﹣a,
则长方形的面积=(15﹣a)a=15a﹣a2.
故选:A.
4.解:依题意得,
×(a+b)×2r﹣π×()2=(a+b)r﹣πr2.
故选:A.
5.解:2x+y,
a2b,,0.5,a是整式,
故选:B.
6.解:根据单项式的定义,可以做出选择:﹣7,﹣
a2bc是单项式.故选:A.
7.解:A、正确的书写格式是,不符合题意;
B、正确的书写格式是,不符合题意;
C、正确的书写格式是a3,不符合题意;
D、符合题意.
故选:D.
8.解:A、﹣xy不一定是负数,故此选项错误;
B、m2﹣2m+3是二次三项式,正确;
C、﹣5是单项式,故此选项错误;
D、πa2b的系数是π,故此选项错误;
故选:B.
9.解:∵第1个图形中点的个数为:1+3=4,
第2个图形中点的个数为:1+3+5=9,
第3个图形中点的个数为:1+3+5+7=16,
…,
∴第n个图形中点的个数为:1+3+5+…+(2n+1)=(n+1)2.
∴第5个图形中所有点的个数为62=36.
故选:C.
10.解:由图可得,
第偶数项对应的数是一些连续的自然数,从2开始,
第奇数项对应的数是一些连续的整数相加,从1开始,
∴a99+a100
=(1+2+3+…+50)+[(100÷2)+1]
=+(50+1)
=1275+51
=1326,
故选:B.
二.填空题
11.解:8a+3b表示的意义是买8本练习本和3支铅笔需要的钱数,
故答案为:买8本练习本和3支铅笔需要的钱数.
12.解:0+1﹣2+3﹣4+5﹣6+…+99﹣100=﹣50,所以落点处离0的距离是50个单位.
故答案为50.
13.解:只含有字母x,y,且次数不超过2的整式:答案不唯一,如3xy,x+y,x2+2xy+y2….
故答案为:答案不唯一,如3xy,x+y,x2+2xy+y2….
14.解:代数式6a2表示的实际意义:棱长为a的正方体的表面积.
故答案为:棱长为a的正方体的表面积.
15.解:1.5x可以解释为这辆火车以速度x行驶了1.5小时的路程.
16.解:2×10+x=20+x.
17.解:首先发现:第一个图案中,有白色的是6个,后边是依次多4个.
所以第n个图案中,是6+4(n﹣1)=4n+2.
∴m与n的函数关系式是m=4n+2.
故答案为:4n+2.
18.解:∵多项式(m+4)x3+xn﹣1﹣5x﹣6是关于x的二次三项式,
∴m+4=0,n﹣1=2,
解得m=﹣4,n=3,
又∵(x﹣2)2≥0,
∴m+n﹣(x﹣2)2的最大值为﹣4+3﹣0=﹣1,
故答案为:﹣1.
19.解:甲数x的5倍与乙数y的的差可以表示为:,
故答案为:,
20.解:根据单项式的系数的定义,单项式﹣5t的系数是﹣5.
三.解答题
21.解:(1)由题意得,
应付车费=1.8×6+0.8×10=18.8(元)>14元,
答:应付车费18.8元;
(2)由题意得,1.5×2+0.8×12=12.6(元)<14元,
∴应付车费=14元,
答:应付车费14元;
(3)根据题意得,他应付车费=1.5×a+0.8×15+0.8×b+0.8×10=(元).
答:他应付车费()元.
22.解:本题答案不唯一.
单项式:,a,3x,4x2ay;
多项式:,a2+x,x+8;
整式:,a,3x,4x2ay,,a2+x,x+8;
分式:.
23.解:①小明家二月份用电量x度,三月份减少20%,则三月份用电量为(1﹣20%)x度;
②a表示立方体的棱长,则a3表示该立方体的体积;
③汽车每小时行驶m千米,行驶30千米所用时间为小时;
④骑车上坡每分钟走a米,下坡每分钟走b米,那么上坡3分钟和下坡2分钟后的平均每分钟走多少米.
24.解:(1)当x=﹣4时,|x﹣1|取得最大值为5,
当x=1时,|x﹣1|取得最小值为0,
∵|x﹣1|的最大值>4,
∴|x﹣1|不是线段AB的吉祥式.
故答案为:5,0,不是;
(2)当﹣4≤x<﹣2时,
|x+2|﹣|x﹣1|﹣1=﹣(x+2)+(x﹣1)﹣1=﹣4,
当﹣2≤x≤1时,
|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2x,
∴﹣4≤2x≤2,
当1≤x≤4时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2,
综上所述:﹣4≤|x+2|﹣|x﹣1|﹣1≤2满足最大值小于等于4,最小值大于等于﹣4,|x+2|﹣|x﹣1|﹣1是线段AB的封闭代数式.
故答案为:②;
(3)|x+1|+2a≤4,,在﹣4和4之间的最小值是,a要不大于这个最小值才能使所有在﹣4和4之间的x都成立,所以a的最大值是,
|x+1|+2a≥﹣4,,在﹣4和4之间的最大值是﹣2,a要不小于这个最大值才能使所有在﹣4和4之间的x都成立,所以a的最小值是﹣2.
25.解:第一个窗户射进的阳光的面积为ab﹣×π()2=ab﹣
第二个窗户射进的阳光的面积为ab﹣2×π()2=ab﹣
∵>
∴第一个窗户射进的阳光的面积<第二个窗户射进的阳光的面积.
26.解:(1)①1×3﹣22=3﹣4=﹣1,
②2×4﹣32=8﹣9=﹣1,
③3×5﹣42=15﹣16=﹣1,
④4×6﹣52=24﹣25=﹣1,
⑤5×7﹣62=35﹣36=﹣1;
(2)第n个式子是:n×(n+2)﹣(n+1)2=﹣1.
故答案为:4×6﹣52=24﹣25=﹣1;n×(n+2)﹣(n+1)2=﹣1.
27.解:(1)按题中图形的排列规律可得:an=3an﹣1+2.
(2)由(1)得:an=3an﹣1+2,an﹣1=3an﹣2+2,两式相减得:
an﹣an﹣1=3(an﹣1﹣an﹣2)①
当n分别取3、4、5、n时,由①式可得下列(n﹣2)个等式:
a3﹣a2=3(a2﹣a1),a4﹣a3=3(a3﹣a2),a5﹣a4=3(a4﹣a3),
an﹣an﹣1=3(an﹣1﹣an﹣2).
显然an﹣an﹣1≠0,以上(n﹣2)个等式的左右两边分别相乘约去相同的项后得:
an﹣an﹣1=3n﹣2(a2﹣a1)②
∵a2﹣a1=17﹣5=12,由(1)又可知an﹣1=(an﹣2),
将它们代入②式即得:an=2×3n﹣1.
代数式》单元测试卷
一.选择题
1.下列说法正确的是( )
A.2a是代数式,1不是代数式
B.代数式表示3﹣b除a
C.当x=4时,代数式的值为0
D.零是最小的整数
2.下列式子,符合代数式书写格式的是( )
A.a+b人
B.1a
C.a×8
D.
3.一个长方形的周长为30cm,若它的一边长用字母a(cm)表示,则它的面积是( )
A.a(15﹣a)cm2
B.a(30﹣a)cm2
C.a(30﹣2a)cm2
D.a(15+a)cm2
4.如图,梯形上、下底分别为a,b,高线长恰好等于圆的直径2r,则图中阴影部分的面积是( )
A.(a+b)r﹣πr2
B.abr﹣πr2
C.2(a+b)r﹣πr2
D.2abr﹣πr2
5.下列代数式中整式有( )
,2x+y,
a2b,,,0.5,a.
A.4个
B.5个
C.6个
D.7个
6.整式2a+b,,﹣7,﹣
a2bc,中,单项式的个数是( )
A.2
B.3
C.4
D.5
7.下列式子,符合书写格式的是( )
A.a÷c
B.1x
C.a?a?a
D.
8.下列说法正确的是( )
A.﹣xy一定是负数
B.m2﹣2m+3是二次三项式
C.﹣5不是单项式
D.的系数是
9.观察下列图形中点的个数,若按其规律再画下去,可以得到第5个图形中所有点的个数为( )
A.16个
B.25个
C.36个
D.49个
10.如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列:a1=1,a2=2.a3=3,a4=3,a5=6,a6=4,a7=10,a8=5…,则a99+a100的值为( )
A.1275
B.1326
C.1378
D.1431
二.填空题
11.若练习本每本a元,铅笔每支b元,那么代数式8a+3b表示的意义是
.
12.一个跳蚤在一条数轴上从原点开始,第一次向右跳1个单位长度,紧接着第二次向左跳2个单位长度,第三次向右跳3个单位长度,第四次向左跳4个单位长度…以此规律跳下去,当它跳第100次落下时,落点处距离原点
个单位长度.
13.请写出一个只含有字母x,y,且次数不超过2的整式:
.
14.代数式6a2的实际意义:
.
15.如果x表示一辆火车行驶的速度,那么1.5x可以解释为
.
16.一个两位数,十位上的数字是2,个位上的数字是x,这个两位数是
.
17.如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式是
.
18.若多项式(m+4)x3+xn﹣1﹣5x﹣6是关于x的二次三项式,则m+n﹣(x﹣2)2的最大值为
.
19.甲数x的5倍与乙数y的的差可以表示为:
.
20.单项式﹣5t的系数是
.
三.解答题
21.滴滴公布了新的滴滴快车计价规则,车费由“总里程费+总时长费”两部分构成,不同时段收费标准不同,具体收费标准如下表,如果车费不足起步价,则按起步价收费.
时间段
里程费(元/千米)
时长费(元/分钟)
起步价(元)
06:00﹣10:00
1.80
0.80
14.00
10:00﹣17:00
1.45
0.40
13.00
17:00﹣21:00
1.50
0.80
14.00
21:00﹣6:00
0.80
0.80
14.00
(1)小明早上7:10乘坐滴滴快车上学,行车里程6千米,行车时间10分钟,则应付车费多少元?
(2)小云17:10放学回家,行车里程2千米,行车时间12分钟,则应付车费多少元?
(3)下晚自习后小明乘坐滴滴快车回家,20:45在学校上车,由于堵车,平均速度是a千米/小时,15分钟后走另外一条路回家,平均速度是b千米/小时,10分钟后到家,则他应付车费多少元?
22.请将下列代数式进行分类(至少三种以上)
,a,3x,,,,a2+x,4x2ay,x+8.
23.请你结合自身生活实际,设计具体情境,解释下列代数式的意义:
①(1﹣20%)x;
②a3;
③;
④.
24.已知如图,在数轴上点A,B所对应的数是﹣4,4.
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于﹣4,则称代数式N,是线段AB的吉祥式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的吉祥式.
问题:
(1)关于x代数式|x﹣1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值是
,取得的最小值是
;所以代数式|x﹣1|
(填是或不是)线段AB的吉祥式.
(2)以下关于x的代数式:
①x2+1;②|x+2|﹣|x﹣1|﹣1,是线段AB的封闭代数式是
.(填序号)
(3)关于x的代数式|x+1|+2a是线段AB的吉祥式,请求出有理数a的最大值和最小值.
25.方方和圆圆的房间窗帘的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径都分别相同),它们的窗户能射进阳光的面积分别是多少(窗框面积不计)谁的窗户射进阳光的面积大?
26.观察下列算式:
①1×3﹣22=3﹣4=﹣1 ②2×4﹣32=8﹣9=﹣1 ③3×5﹣42=15﹣16=﹣1
(1)请你按照三个算式的规律写出第④个、第⑤个算式;
(2)把这个规律用含字母的式子表示出来,并说明其正确性.
27.观察下列图形:
如果按这个规律一直排到第n个图形,请探究下列问题:
(1)设第n个图形和第n﹣1个图形中所有三角形的个数分别为an、an﹣1,问:它们之间有什么数量关系?请写出这个关系式.
(2)请你用含n的代数式来表示an,并证明你的结论.
参考答案与试题解析
一.选择题
1.解:单独的数或字母都是代数式,故A不正确;
代数式表示3﹣b除以a或3﹣b与a的商,故B不正确;
C正确;
整数包括正整数、0、负整数,故D不正确.
故选:C.
2.解:A、a+b人的正确书写格式是(a+b)人,故本选项错误;
B、1a的正确书写格式是a,故本选项错误;
C、a×8的正确书写形式是8a,故本选项错误;
D、符合代数式的书写要求,故本选项正确;
故选:D.
3.解:另一边长=×30﹣a=15﹣a,
则长方形的面积=(15﹣a)a=15a﹣a2.
故选:A.
4.解:依题意得,
×(a+b)×2r﹣π×()2=(a+b)r﹣πr2.
故选:A.
5.解:2x+y,
a2b,,0.5,a是整式,
故选:B.
6.解:根据单项式的定义,可以做出选择:﹣7,﹣
a2bc是单项式.故选:A.
7.解:A、正确的书写格式是,不符合题意;
B、正确的书写格式是,不符合题意;
C、正确的书写格式是a3,不符合题意;
D、符合题意.
故选:D.
8.解:A、﹣xy不一定是负数,故此选项错误;
B、m2﹣2m+3是二次三项式,正确;
C、﹣5是单项式,故此选项错误;
D、πa2b的系数是π,故此选项错误;
故选:B.
9.解:∵第1个图形中点的个数为:1+3=4,
第2个图形中点的个数为:1+3+5=9,
第3个图形中点的个数为:1+3+5+7=16,
…,
∴第n个图形中点的个数为:1+3+5+…+(2n+1)=(n+1)2.
∴第5个图形中所有点的个数为62=36.
故选:C.
10.解:由图可得,
第偶数项对应的数是一些连续的自然数,从2开始,
第奇数项对应的数是一些连续的整数相加,从1开始,
∴a99+a100
=(1+2+3+…+50)+[(100÷2)+1]
=+(50+1)
=1275+51
=1326,
故选:B.
二.填空题
11.解:8a+3b表示的意义是买8本练习本和3支铅笔需要的钱数,
故答案为:买8本练习本和3支铅笔需要的钱数.
12.解:0+1﹣2+3﹣4+5﹣6+…+99﹣100=﹣50,所以落点处离0的距离是50个单位.
故答案为50.
13.解:只含有字母x,y,且次数不超过2的整式:答案不唯一,如3xy,x+y,x2+2xy+y2….
故答案为:答案不唯一,如3xy,x+y,x2+2xy+y2….
14.解:代数式6a2表示的实际意义:棱长为a的正方体的表面积.
故答案为:棱长为a的正方体的表面积.
15.解:1.5x可以解释为这辆火车以速度x行驶了1.5小时的路程.
16.解:2×10+x=20+x.
17.解:首先发现:第一个图案中,有白色的是6个,后边是依次多4个.
所以第n个图案中,是6+4(n﹣1)=4n+2.
∴m与n的函数关系式是m=4n+2.
故答案为:4n+2.
18.解:∵多项式(m+4)x3+xn﹣1﹣5x﹣6是关于x的二次三项式,
∴m+4=0,n﹣1=2,
解得m=﹣4,n=3,
又∵(x﹣2)2≥0,
∴m+n﹣(x﹣2)2的最大值为﹣4+3﹣0=﹣1,
故答案为:﹣1.
19.解:甲数x的5倍与乙数y的的差可以表示为:,
故答案为:,
20.解:根据单项式的系数的定义,单项式﹣5t的系数是﹣5.
三.解答题
21.解:(1)由题意得,
应付车费=1.8×6+0.8×10=18.8(元)>14元,
答:应付车费18.8元;
(2)由题意得,1.5×2+0.8×12=12.6(元)<14元,
∴应付车费=14元,
答:应付车费14元;
(3)根据题意得,他应付车费=1.5×a+0.8×15+0.8×b+0.8×10=(元).
答:他应付车费()元.
22.解:本题答案不唯一.
单项式:,a,3x,4x2ay;
多项式:,a2+x,x+8;
整式:,a,3x,4x2ay,,a2+x,x+8;
分式:.
23.解:①小明家二月份用电量x度,三月份减少20%,则三月份用电量为(1﹣20%)x度;
②a表示立方体的棱长,则a3表示该立方体的体积;
③汽车每小时行驶m千米,行驶30千米所用时间为小时;
④骑车上坡每分钟走a米,下坡每分钟走b米,那么上坡3分钟和下坡2分钟后的平均每分钟走多少米.
24.解:(1)当x=﹣4时,|x﹣1|取得最大值为5,
当x=1时,|x﹣1|取得最小值为0,
∵|x﹣1|的最大值>4,
∴|x﹣1|不是线段AB的吉祥式.
故答案为:5,0,不是;
(2)当﹣4≤x<﹣2时,
|x+2|﹣|x﹣1|﹣1=﹣(x+2)+(x﹣1)﹣1=﹣4,
当﹣2≤x≤1时,
|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2x,
∴﹣4≤2x≤2,
当1≤x≤4时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2,
综上所述:﹣4≤|x+2|﹣|x﹣1|﹣1≤2满足最大值小于等于4,最小值大于等于﹣4,|x+2|﹣|x﹣1|﹣1是线段AB的封闭代数式.
故答案为:②;
(3)|x+1|+2a≤4,,在﹣4和4之间的最小值是,a要不大于这个最小值才能使所有在﹣4和4之间的x都成立,所以a的最大值是,
|x+1|+2a≥﹣4,,在﹣4和4之间的最大值是﹣2,a要不小于这个最大值才能使所有在﹣4和4之间的x都成立,所以a的最小值是﹣2.
25.解:第一个窗户射进的阳光的面积为ab﹣×π()2=ab﹣
第二个窗户射进的阳光的面积为ab﹣2×π()2=ab﹣
∵>
∴第一个窗户射进的阳光的面积<第二个窗户射进的阳光的面积.
26.解:(1)①1×3﹣22=3﹣4=﹣1,
②2×4﹣32=8﹣9=﹣1,
③3×5﹣42=15﹣16=﹣1,
④4×6﹣52=24﹣25=﹣1,
⑤5×7﹣62=35﹣36=﹣1;
(2)第n个式子是:n×(n+2)﹣(n+1)2=﹣1.
故答案为:4×6﹣52=24﹣25=﹣1;n×(n+2)﹣(n+1)2=﹣1.
27.解:(1)按题中图形的排列规律可得:an=3an﹣1+2.
(2)由(1)得:an=3an﹣1+2,an﹣1=3an﹣2+2,两式相减得:
an﹣an﹣1=3(an﹣1﹣an﹣2)①
当n分别取3、4、5、n时,由①式可得下列(n﹣2)个等式:
a3﹣a2=3(a2﹣a1),a4﹣a3=3(a3﹣a2),a5﹣a4=3(a4﹣a3),
an﹣an﹣1=3(an﹣1﹣an﹣2).
显然an﹣an﹣1≠0,以上(n﹣2)个等式的左右两边分别相乘约去相同的项后得:
an﹣an﹣1=3n﹣2(a2﹣a1)②
∵a2﹣a1=17﹣5=12,由(1)又可知an﹣1=(an﹣2),
将它们代入②式即得:an=2×3n﹣1.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
