8.1 基本立体图形(第1课时)课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册25张PPT
文档属性
| 名称 | 8.1 基本立体图形(第1课时)课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册25张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 15:52:07 | ||
图片预览




文档简介
学习对象
学习内容
学习的基本方法
阅读第八章章引言P96
本章我们要学什么?怎么学?
形状,大小,位置关系
抽象,看,画,证,算
20210402
问题1 小学、初中我们学过哪些立体图形?你能在下图中找到吗?
新课讲授
实物
立体图形
长方体
圆柱体
球体
圆锥体
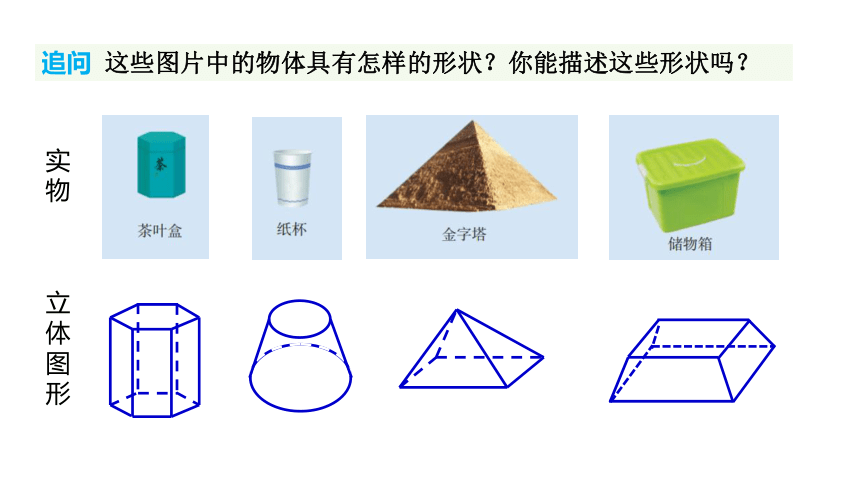
追问 这些图片中的物体具有怎样的形状?你能描述这些形状吗?
实物
立体图形
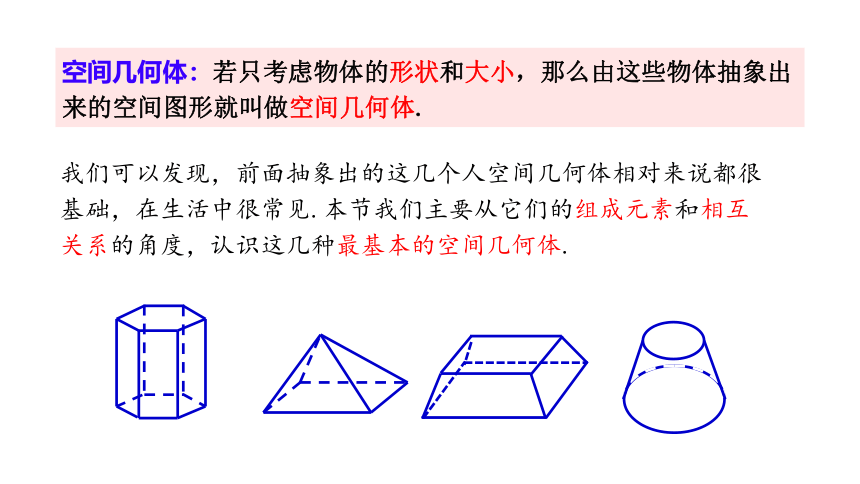
空间几何体:若只考虑物体的形状和大小,那么由这些物体抽象出来的空间图形就叫做空间几何体.
我们可以发现,前面抽象出的这几个人空间几何体相对来说都很基础,在生活中很常见.本节我们主要从它们的组成元素和相互关系的角度,认识这几种最基本的空间几何体.
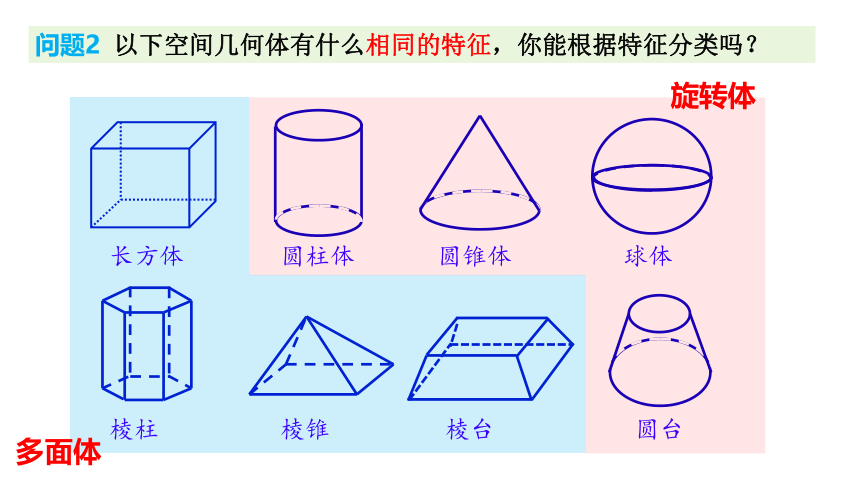
问题2 以下空间几何体有什么相同的特征,你能根据特征分类吗?
旋转体
多面体
长方体
圆柱体
球体
圆锥体
棱柱
棱锥
圆台
棱台
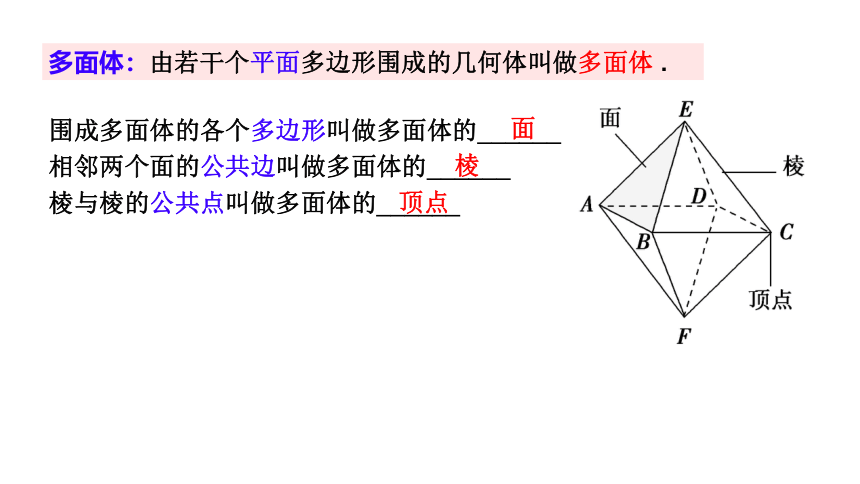
多面体:由若干个平面多边形围成的几何体叫做多面体 .
围成多面体的各个多边形叫做多面体的______
相邻两个面的公共边叫做多面体的______
棱与棱的公共点叫做多面体的______
面
棱
顶点
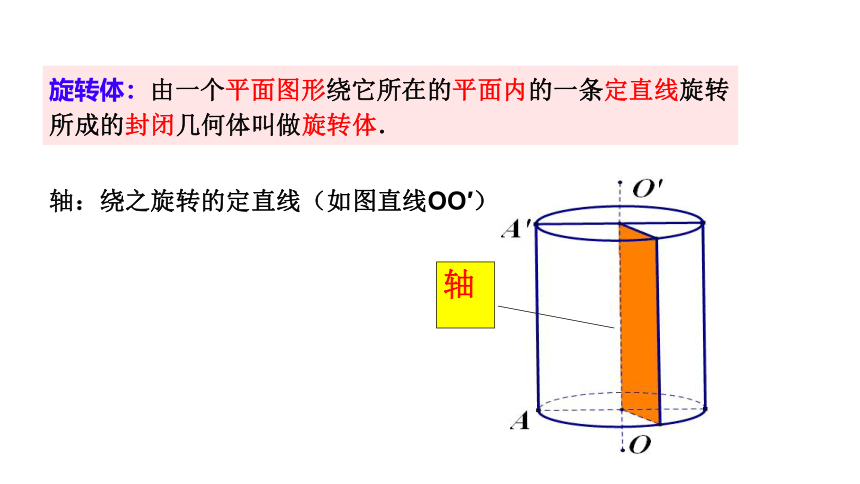
轴:绕之旋转的定直线(如图直线OO′)
轴
旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所成的封闭几何体叫做旋转体.
问题3 以下的多面体称作棱柱,什么是棱柱?
一个多面体有两个面 __,其余各面都是 ,并且相邻两个四边形的公共边都 ,这样的多面体叫做_____.
1.棱柱的概念
互相平行
四边形
棱柱
互相平行
多面体——1:棱柱
A
B
C
D
E
A’
B’
C’
D’
E’
底
底
两个互相平行的面叫做棱柱的底面
其余各面叫做棱柱的侧面
相邻侧面的公共边叫做棱柱的侧棱
侧面与底面的公共顶点叫做棱柱的顶点
·
·
·
·
·
·
·
·
·
·
3.棱柱的表示法
棱柱ABCDE- A1B1C1D1E1
(1)底面互相平行且全等.
(2)侧面都是平行四边形.
(3)侧棱平行且相等.
2.棱柱的结构特征
思考1:有两个面互相平行,其余各面都是四边形的几何体是棱柱吗?
思考2:有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
答:不一定是
答:不一定是
①按棱柱底面边数分类:
三棱柱、四棱柱、五棱柱、......
4.棱柱的分类
平行六面体:底面是平行四边形的四棱柱
②按棱柱侧棱与底面位置关系分类:
直棱柱:
正棱柱:底面是正多边形的直棱柱
斜棱柱:
有一面是 ,其余各面都是有一个 的三角形,由这些面所围成的多面体叫做棱锥.
多边形
公共顶点
多面体——2:棱锥
1.棱锥的概念
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
2.棱锥的结构特征
(1)底面是一个多边形.
(2)侧面都是三角形.
(3)各侧面有一个公共顶点.
用表示顶点和底面的字母表示,如四棱锥S-ABCD.
3.棱锥的表示法
4.棱锥的分类
正棱锥:底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
分类标准:底面多边形的边数
三棱锥
(四面体)
四棱锥
五棱锥
六棱锥
S
A
B
C
用一个 的平面去截 , 之间的部分叫做棱台.
平行于棱锥底面
棱锥
底面和截面
多面体——3:棱台
1.棱台的概念
下底面
上底面
侧面
侧棱
顶点
用平行的两底面多边形的字母表示棱台,如:
棱台ABC- A’B’C’
A
C
B
3.棱台的表示方法
2.棱台的结构特征
(1)上下底面互相平行且是相似图形.
(2)各侧棱的延长线交于一点.
(3)各侧面为梯形.
三棱台、四棱台、五棱台、......
4.棱台的分类
分类标准:底面多边形的边数
多面体
例题1 将下列各类几何体之间的关系用Venn图表示出来:
多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体.
棱锥
四面体
直棱柱
平行六面体
棱台
棱柱
长方体
2、棱柱、棱台、棱锥之间有什么关系吗?
1、棱柱、棱台、棱锥定义是怎样的?
课堂小结
3、观察立体图形的思路?
整体——局部——整体
1.下列关于棱柱的说法错误的是( )
A.所有棱柱的两个底面都平行
B.所有的棱柱一定有两个面互相平行,其余每相邻面的公共边互相平行
C.有两个面互相平行,其余各面都是四边形的几何体一定是棱柱
D.棱柱至少有五个面
C
2、如图所示,多面体ABCD-A'B'C'D'是棱台吗?
3.判断正误
(1)棱柱的侧面都是平行四边形.( )
(2)有一个面是多边形,其余各面都是三角形的几何体叫棱锥.( )
(3)用一平面去截棱锥底面和截面之间的部分叫棱台.( )
[答案] (1)√ (2)× (3)×
4.有一个多面体,共有四个面围成,每一个面都是三角形,则这个几何体为( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
D
5.下列关于棱锥、棱台的说法:
①棱台的侧面一定不会是平行四边形;
②棱锥的侧面只能是三角形;
③由四个面围成的封闭图形只能是三棱锥;
④棱锥被平面截成的两部分不可能都是棱锥.
其中正确说法的序号是 .
①②③
学习内容
学习的基本方法
阅读第八章章引言P96
本章我们要学什么?怎么学?
形状,大小,位置关系
抽象,看,画,证,算
20210402
问题1 小学、初中我们学过哪些立体图形?你能在下图中找到吗?
新课讲授
实物
立体图形
长方体
圆柱体
球体
圆锥体
追问 这些图片中的物体具有怎样的形状?你能描述这些形状吗?
实物
立体图形
空间几何体:若只考虑物体的形状和大小,那么由这些物体抽象出来的空间图形就叫做空间几何体.
我们可以发现,前面抽象出的这几个人空间几何体相对来说都很基础,在生活中很常见.本节我们主要从它们的组成元素和相互关系的角度,认识这几种最基本的空间几何体.
问题2 以下空间几何体有什么相同的特征,你能根据特征分类吗?
旋转体
多面体
长方体
圆柱体
球体
圆锥体
棱柱
棱锥
圆台
棱台
多面体:由若干个平面多边形围成的几何体叫做多面体 .
围成多面体的各个多边形叫做多面体的______
相邻两个面的公共边叫做多面体的______
棱与棱的公共点叫做多面体的______
面
棱
顶点
轴:绕之旋转的定直线(如图直线OO′)
轴
旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所成的封闭几何体叫做旋转体.
问题3 以下的多面体称作棱柱,什么是棱柱?
一个多面体有两个面 __,其余各面都是 ,并且相邻两个四边形的公共边都 ,这样的多面体叫做_____.
1.棱柱的概念
互相平行
四边形
棱柱
互相平行
多面体——1:棱柱
A
B
C
D
E
A’
B’
C’
D’
E’
底
底
两个互相平行的面叫做棱柱的底面
其余各面叫做棱柱的侧面
相邻侧面的公共边叫做棱柱的侧棱
侧面与底面的公共顶点叫做棱柱的顶点
·
·
·
·
·
·
·
·
·
·
3.棱柱的表示法
棱柱ABCDE- A1B1C1D1E1
(1)底面互相平行且全等.
(2)侧面都是平行四边形.
(3)侧棱平行且相等.
2.棱柱的结构特征
思考1:有两个面互相平行,其余各面都是四边形的几何体是棱柱吗?
思考2:有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
答:不一定是
答:不一定是
①按棱柱底面边数分类:
三棱柱、四棱柱、五棱柱、......
4.棱柱的分类
平行六面体:底面是平行四边形的四棱柱
②按棱柱侧棱与底面位置关系分类:
直棱柱:
正棱柱:底面是正多边形的直棱柱
斜棱柱:
有一面是 ,其余各面都是有一个 的三角形,由这些面所围成的多面体叫做棱锥.
多边形
公共顶点
多面体——2:棱锥
1.棱锥的概念
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
2.棱锥的结构特征
(1)底面是一个多边形.
(2)侧面都是三角形.
(3)各侧面有一个公共顶点.
用表示顶点和底面的字母表示,如四棱锥S-ABCD.
3.棱锥的表示法
4.棱锥的分类
正棱锥:底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
分类标准:底面多边形的边数
三棱锥
(四面体)
四棱锥
五棱锥
六棱锥
S
A
B
C
用一个 的平面去截 , 之间的部分叫做棱台.
平行于棱锥底面
棱锥
底面和截面
多面体——3:棱台
1.棱台的概念
下底面
上底面
侧面
侧棱
顶点
用平行的两底面多边形的字母表示棱台,如:
棱台ABC- A’B’C’
A
C
B
3.棱台的表示方法
2.棱台的结构特征
(1)上下底面互相平行且是相似图形.
(2)各侧棱的延长线交于一点.
(3)各侧面为梯形.
三棱台、四棱台、五棱台、......
4.棱台的分类
分类标准:底面多边形的边数
多面体
例题1 将下列各类几何体之间的关系用Venn图表示出来:
多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体.
棱锥
四面体
直棱柱
平行六面体
棱台
棱柱
长方体
2、棱柱、棱台、棱锥之间有什么关系吗?
1、棱柱、棱台、棱锥定义是怎样的?
课堂小结
3、观察立体图形的思路?
整体——局部——整体
1.下列关于棱柱的说法错误的是( )
A.所有棱柱的两个底面都平行
B.所有的棱柱一定有两个面互相平行,其余每相邻面的公共边互相平行
C.有两个面互相平行,其余各面都是四边形的几何体一定是棱柱
D.棱柱至少有五个面
C
2、如图所示,多面体ABCD-A'B'C'D'是棱台吗?
3.判断正误
(1)棱柱的侧面都是平行四边形.( )
(2)有一个面是多边形,其余各面都是三角形的几何体叫棱锥.( )
(3)用一平面去截棱锥底面和截面之间的部分叫棱台.( )
[答案] (1)√ (2)× (3)×
4.有一个多面体,共有四个面围成,每一个面都是三角形,则这个几何体为( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
D
5.下列关于棱锥、棱台的说法:
①棱台的侧面一定不会是平行四边形;
②棱锥的侧面只能是三角形;
③由四个面围成的封闭图形只能是三棱锥;
④棱锥被平面截成的两部分不可能都是棱锥.
其中正确说法的序号是 .
①②③
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
