8.6.2直线与平面垂直(第1课时)课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册14张PPT
文档属性
| 名称 | 8.6.2直线与平面垂直(第1课时)课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册14张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 16:13:00 | ||
图片预览





文档简介
学习目标
1.领会直线与平面垂直的定义,了解直线与平面所成的角;
2.掌握直线与平面垂直的判定定理与性质定理;
3.会用相关定义、定理解决直线与平面垂直问题.
4.核心素养:直观想象,数学抽象,逻辑推理.
空间中直线与平面有几种位置关系?
线 面
位置关系
垂直
斜交
a
b
在平面内
平行
复习回顾
——第一课时
新课导入
旗杆与地面垂直
旗杆AB所在直线与地面垂直,即与地面上任意一条直线都垂直.
旗杆所在的直线AB与其影子BC所在直线是否保持垂直?
垂直
旗杆AB所在直线于地面上任意一条过点B的直线垂直.
地面上不过点B的任意直线B’C’,AB与B’C’垂直吗?
思考1:
记作:
新课讲授
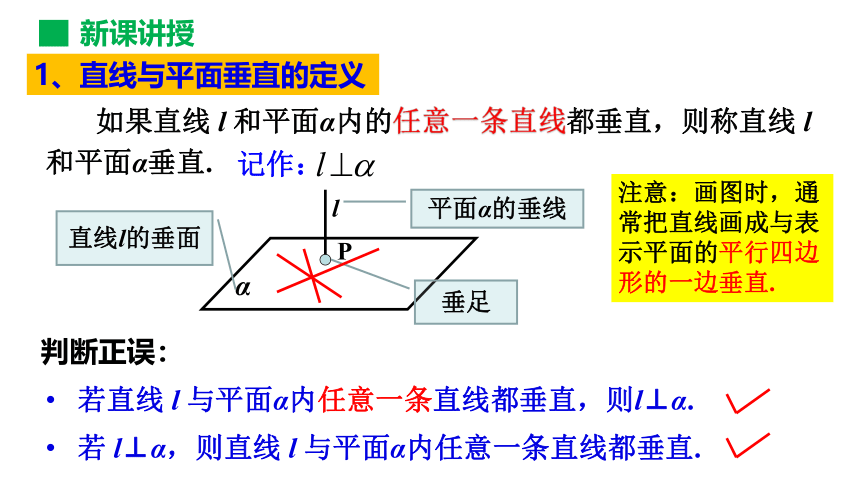
如果直线 l 和平面α内的任意一条直线都垂直,则称直线 l 和平面α垂直.
α
P
1、直线与平面垂直的定义
l
注意:画图时,通常把直线画成与表示平面的平行四边形的一边垂直.
平面α的垂线
垂足
直线l的垂面
若直线 l 与平面α内任意一条直线都垂直,则l⊥α.
若 l⊥α,则直线 l 与平面α内任意一条直线都垂直.
判断正误:
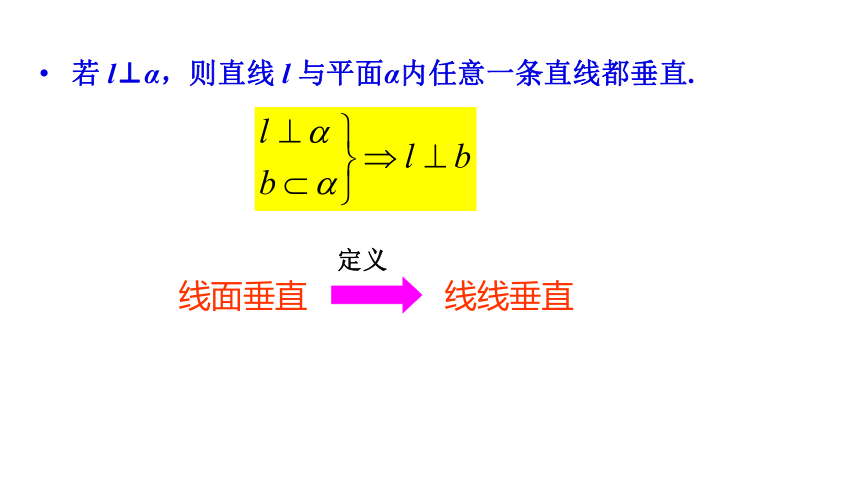
若 l⊥α,则直线 l 与平面α内任意一条直线都垂直.
线面垂直
线线垂直
定义
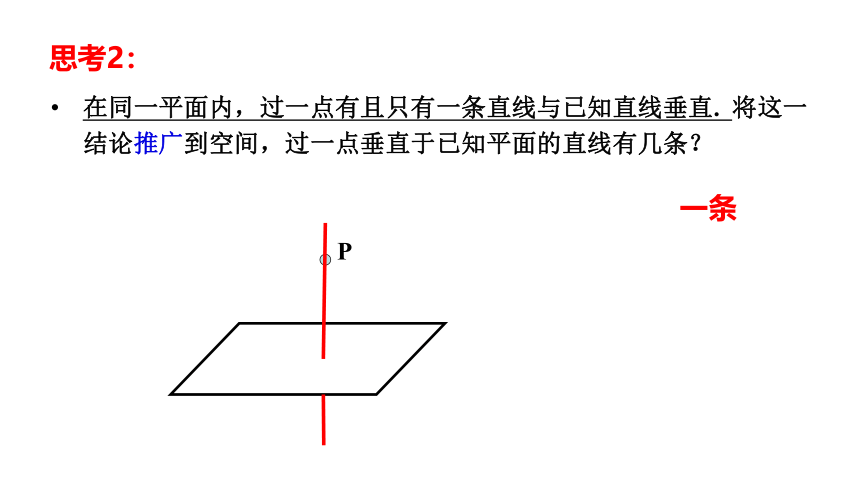
思考2:
在同一平面内,过一点有且只有一条直线与已知直线垂直. 将这一结论推广到空间,过一点垂直于已知平面的直线有几条?
P
一条
l
α
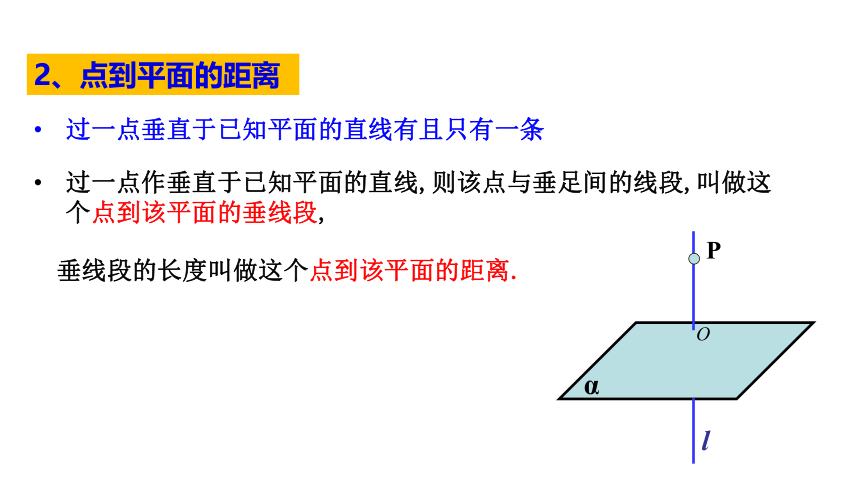
过一点垂直于已知平面的直线有且只有一条
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,
垂线段的长度叫做这个点到该平面的距离.
2、点到平面的距离
P
l
能否利用在平面内找有限条直线与已知直线垂直,从而判定直线与平面垂直?
一条?
怎么来判定直线与平面垂直?
由定义判定直线与平面垂直,简便吗?
思考3:
l
l
两条?
探究:准备一块三角形纸片,设纸片的三个顶角分别为A,B,C,过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上( 使BD、DC与桌面都接触).
思考:(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在的平面垂直?
当且仅当折痕AD 是BC 边上的高时,AD 所在直线与桌面所在平面α垂直.
事实上,由基本事实的推论2,平面α可以看成是由两条相交直线BD,CD所唯一确定的,所以当直线AD垂直于这两条相交直线时,就能保证直线AD与α内所有直线都垂直。
一条直线和一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
线线垂直 线面垂直
判定定理
定义
垂直
内
相交
3、直线和平面垂直的判定定理
如图,已知 ,求证:
∵
∴
∵
是两条相交直线,
∴
证明:在平面 内作两条相交直线m,n
∵ ,
例题巩固
∴
例题1 求证:若两条平行直线中的一条直线垂直于一个平面,那么另一条直线垂直于这个平面.
方法1:利用线面垂直的判定定理证明
方法2:利用线面垂直的定义证明
∵
∴
∵m是平面α内任意一条直线
∴
证明:在平面 内任取一条直线m
∵ ,
∴
若两条平行直线中的一条直线垂直于一个平面,那么另一条直线垂直于这个平面.
例题2 如图,点P 是平行四边形ABCD 所在平面外一点,O 是对角线AC与BD的交点,且PA =PC,PB =PD.
求证:PO⊥平面ABCD
C
A
B
D
O
P
=
ABCD
PO
O
BD
AC
平面
又
^
\
I
Q
BD
PO
BD
O
PD
PB
的中点
是
点
又
^
\
=
Q
,
PC
PA
=
AC
PO
点O是AC的中点
证明:
^
\
Q
,
例题3
例题4 在正方体ABCD-A1B1C1D1中,求证BC1⊥平面A1B1CD .
A
B
C
D
A1
B1
C1
D1
O
解:
∴A1B1⊥BC1
∵BC1⊥B1C
B1C和A1B1平面A1B1CD内的两条相交直线
∴BC1⊥平面A1B1CD
∵正方体A1B1C1D1-ABCD
∴A1B1⊥平面B1BCC1
∵BC1 平面B1BCC1
例题5 如图,直四棱柱 中,底面四边形 满足什么条件时, ?
底面四边形ABCD对角线相互垂直
课堂小结
1. 直线与平面垂直的定义:“任意”
2. 直线和平面垂直的判定定理
定义的运用:线面垂直
线线垂直
关键:在平面内找到两条相交直线与已知直线垂直
线线垂直
线面垂直
3.
如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足.
P
A
斜足
斜线
平面的斜线
思考4 我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,如何给它命名?此时又该如何刻画直线和平面的这种关系呢?
如图,过斜线上斜足以外的一点向平面引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.
平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角,如图中∠PAO.
斜线
斜足
射影
垂足
垂线
一条直线垂直于平面,我们说它所成的角是直角;
一条直线和平面平行,或在平面内,我们说它所成的角是0°的角.
规定:
直线与平面所成的角θ的取值范围是什么?
4、直线和平面所成角
例题1 如图,正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2)A1C1与面BB1D1D所成的角
(1)0o
(2)90o
例题1 如图,正方体ABCD-A1B1C1D1中,求:
(3) A1C1与面BB1C1C所成的角
(4)A1B与面A1B1CD所成的角
(4)30o
(3)45o
O
例题1 (4)求A1B与面A1B1CD所成的角
O
1.构造:作垂线→作射影→作平面角
2.证明:证明某平面角就是斜线与平面所成角(关键证垂直)
3.计算:求所成角,通常在垂线段、斜线和射影所构成的直角三角形中计算.
4.下结论
1.领会直线与平面垂直的定义,了解直线与平面所成的角;
2.掌握直线与平面垂直的判定定理与性质定理;
3.会用相关定义、定理解决直线与平面垂直问题.
4.核心素养:直观想象,数学抽象,逻辑推理.
空间中直线与平面有几种位置关系?
线 面
位置关系
垂直
斜交
a
b
在平面内
平行
复习回顾
——第一课时
新课导入
旗杆与地面垂直
旗杆AB所在直线与地面垂直,即与地面上任意一条直线都垂直.
旗杆所在的直线AB与其影子BC所在直线是否保持垂直?
垂直
旗杆AB所在直线于地面上任意一条过点B的直线垂直.
地面上不过点B的任意直线B’C’,AB与B’C’垂直吗?
思考1:
记作:
新课讲授
如果直线 l 和平面α内的任意一条直线都垂直,则称直线 l 和平面α垂直.
α
P
1、直线与平面垂直的定义
l
注意:画图时,通常把直线画成与表示平面的平行四边形的一边垂直.
平面α的垂线
垂足
直线l的垂面
若直线 l 与平面α内任意一条直线都垂直,则l⊥α.
若 l⊥α,则直线 l 与平面α内任意一条直线都垂直.
判断正误:
若 l⊥α,则直线 l 与平面α内任意一条直线都垂直.
线面垂直
线线垂直
定义
思考2:
在同一平面内,过一点有且只有一条直线与已知直线垂直. 将这一结论推广到空间,过一点垂直于已知平面的直线有几条?
P
一条
l
α
过一点垂直于已知平面的直线有且只有一条
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,
垂线段的长度叫做这个点到该平面的距离.
2、点到平面的距离
P
l
能否利用在平面内找有限条直线与已知直线垂直,从而判定直线与平面垂直?
一条?
怎么来判定直线与平面垂直?
由定义判定直线与平面垂直,简便吗?
思考3:
l
l
两条?
探究:准备一块三角形纸片,设纸片的三个顶角分别为A,B,C,过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上( 使BD、DC与桌面都接触).
思考:(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在的平面垂直?
当且仅当折痕AD 是BC 边上的高时,AD 所在直线与桌面所在平面α垂直.
事实上,由基本事实的推论2,平面α可以看成是由两条相交直线BD,CD所唯一确定的,所以当直线AD垂直于这两条相交直线时,就能保证直线AD与α内所有直线都垂直。
一条直线和一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
线线垂直 线面垂直
判定定理
定义
垂直
内
相交
3、直线和平面垂直的判定定理
如图,已知 ,求证:
∵
∴
∵
是两条相交直线,
∴
证明:在平面 内作两条相交直线m,n
∵ ,
例题巩固
∴
例题1 求证:若两条平行直线中的一条直线垂直于一个平面,那么另一条直线垂直于这个平面.
方法1:利用线面垂直的判定定理证明
方法2:利用线面垂直的定义证明
∵
∴
∵m是平面α内任意一条直线
∴
证明:在平面 内任取一条直线m
∵ ,
∴
若两条平行直线中的一条直线垂直于一个平面,那么另一条直线垂直于这个平面.
例题2 如图,点P 是平行四边形ABCD 所在平面外一点,O 是对角线AC与BD的交点,且PA =PC,PB =PD.
求证:PO⊥平面ABCD
C
A
B
D
O
P
=
ABCD
PO
O
BD
AC
平面
又
^
\
I
Q
BD
PO
BD
O
PD
PB
的中点
是
点
又
^
\
=
Q
,
PC
PA
=
AC
PO
点O是AC的中点
证明:
^
\
Q
,
例题3
例题4 在正方体ABCD-A1B1C1D1中,求证BC1⊥平面A1B1CD .
A
B
C
D
A1
B1
C1
D1
O
解:
∴A1B1⊥BC1
∵BC1⊥B1C
B1C和A1B1平面A1B1CD内的两条相交直线
∴BC1⊥平面A1B1CD
∵正方体A1B1C1D1-ABCD
∴A1B1⊥平面B1BCC1
∵BC1 平面B1BCC1
例题5 如图,直四棱柱 中,底面四边形 满足什么条件时, ?
底面四边形ABCD对角线相互垂直
课堂小结
1. 直线与平面垂直的定义:“任意”
2. 直线和平面垂直的判定定理
定义的运用:线面垂直
线线垂直
关键:在平面内找到两条相交直线与已知直线垂直
线线垂直
线面垂直
3.
如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足.
P
A
斜足
斜线
平面的斜线
思考4 我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,如何给它命名?此时又该如何刻画直线和平面的这种关系呢?
如图,过斜线上斜足以外的一点向平面引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.
平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角,如图中∠PAO.
斜线
斜足
射影
垂足
垂线
一条直线垂直于平面,我们说它所成的角是直角;
一条直线和平面平行,或在平面内,我们说它所成的角是0°的角.
规定:
直线与平面所成的角θ的取值范围是什么?
4、直线和平面所成角
例题1 如图,正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2)A1C1与面BB1D1D所成的角
(1)0o
(2)90o
例题1 如图,正方体ABCD-A1B1C1D1中,求:
(3) A1C1与面BB1C1C所成的角
(4)A1B与面A1B1CD所成的角
(4)30o
(3)45o
O
例题1 (4)求A1B与面A1B1CD所成的角
O
1.构造:作垂线→作射影→作平面角
2.证明:证明某平面角就是斜线与平面所成角(关键证垂直)
3.计算:求所成角,通常在垂线段、斜线和射影所构成的直角三角形中计算.
4.下结论
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
