沪科版数学九年级上册21.3 二次函数与一元二次方程新授课件(共25张PPT)
文档属性
| 名称 | 沪科版数学九年级上册21.3 二次函数与一元二次方程新授课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
21.3
二次函数与一元二次方程的关系
情景导入
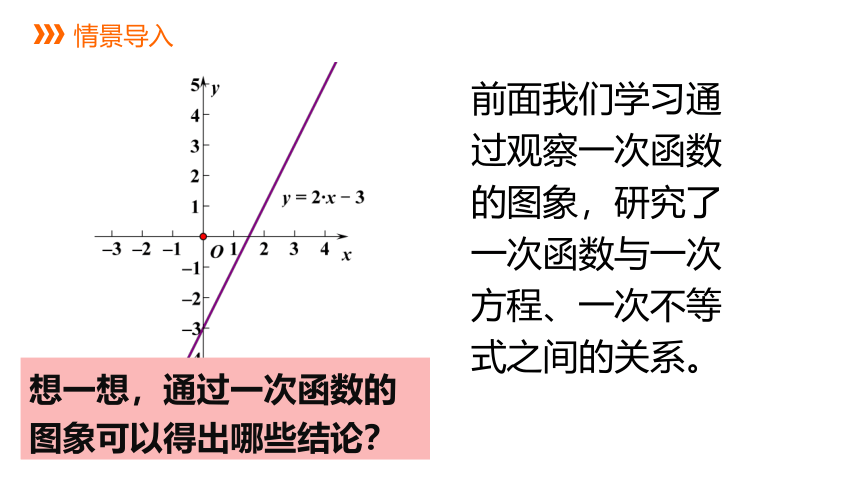
前面我们学习通过观察一次函数的图象,研究了一次函数与一次方程、一次不等式之间的关系。
想一想,通过一次函数的图象可以得出哪些结论?
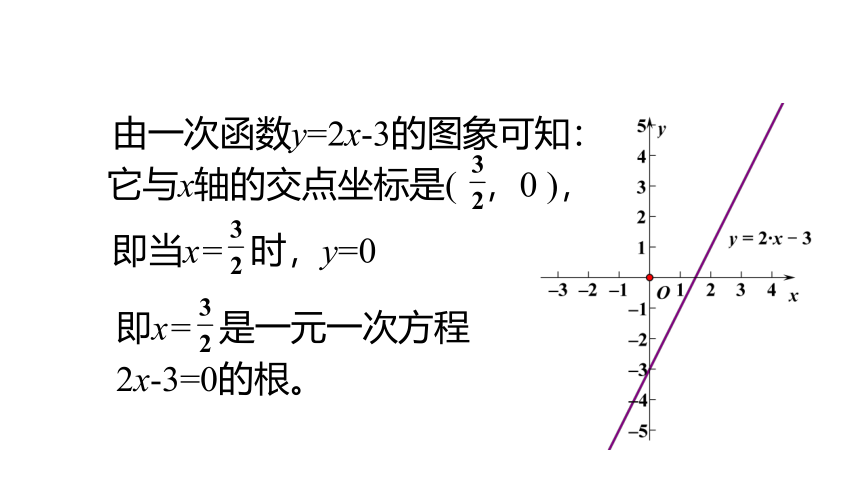
由一次函数y=2x-3的图象可知:
它与x轴的交点坐标是(
,0
),
即当x=
时,y=0
即x=
是一元一次方程
2x-3=0的根。
当x>
时,图象在x轴上方即y>0,
所以x>
为一元一次不等式
2x-3>0的解集;
当x<
时,图象在x轴下方即y<0,
所以x<
为一元一次不等式
2x-3<0的解集.
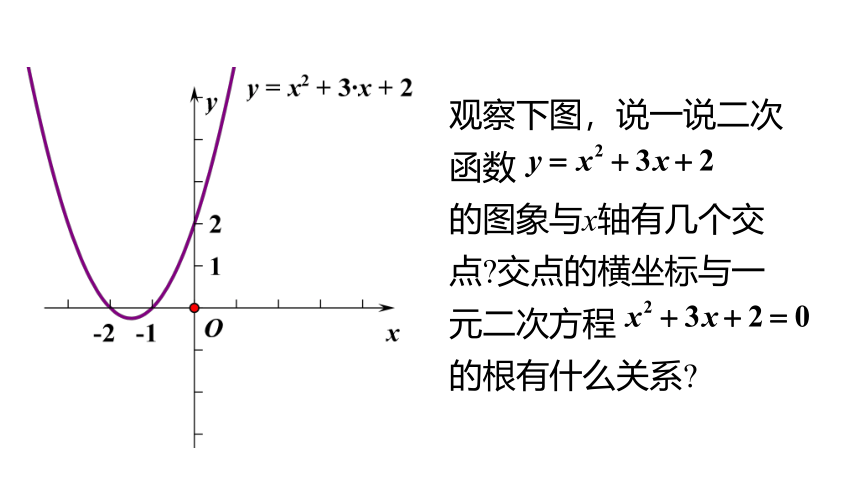
观察下图,说一说二次函数
的图象与x轴有几个交点?交点的横坐标与一元二次方程
的根有什么关系?
观察图象可知,二次函数
的图象与x轴有两个交点。两交点分别为(-2,0)(-1,0),交点横坐标可看作是方程
的根。
根据上述问题3
画出的图象,继续回答下列问题:
(1)当x取何值时,y<0?当x取何值时,y>0?
(2)试用含有x的不等式来描述问题(1)。
通过解答以上问题,想一想,二次函数与一元二次方程与一元二次不等式有什么联系?
解:
(1)
(2)
试一试
对于一元二次方程
,
当
时有实数根,这个实数根就是对应二次函数
的值等于0时自变量x的一个值,即二次函数的图象与x轴一个交点的横坐标。
二次函数与一元二次方程是紧密联系又相互渗透的,两者经常综合命题
1.二次函数y=ax2+bx+c,当y=0(或其他数值m)时,就变
成了一元二次方程ax2+bx+c=0(或m).
2.二次函数y=ax2+bx+c的图象与轴的交点情况有三种:
有两个交点,有一个交点,没有交点.如果抛物线y=ax2
+bx+c与x轴交于两点(x1,0)
(x2,0)则x1,x2是一元二
次方程ax2+bx+c=0的两个不等实根,反之亦成立.
3.抛物线y=ax2+bx+c与x轴交于两点
一元二次方程ax2+bx+c=0有两个不相等的实数根
b2-4ac
>0;抛物线y=ax2+bx+c与x轴只有一个交点
一元二次方程ax2+bx+c=0有两个相等的实数根
b2-4ac
=0;抛物线y=ax2+bx+c与x轴没有交点
一元二次方程ax2+bx+c=0没有实数根
b2-4ac
<
0.
例题讲解
例
用图象法求一元二次方程x2+2x-1=0的近似解(精确到0.1).
由图象可知,方程有两个实数根,一个在-3和-2之间.另—个在0和1之间.
先求位于-3和-2之间的根.
x
…
-2.6
-2.5
-2.4
-2.3
…
y
…
…
0.56
0.25
-0.04
-0.31
观察x取何值时,y值最接近0?
先求位于-3和-2之间的根.
x
…
-2.6
-2.5
-2.4
-2.3
…
y
…
…
0.56
0.25
-0.04
-0.31
观察上表可以发现,当x分别取-2.5和-2.4时,对应的y由正变负,可见在-2.5与-2.4之间有一个x使y=0,即有方程
的一个根。
请同学们仿照上面的方法,求出上述方程精确到0.1的另一个根.
函数y=ax2+bx+c与直线y=kx+d的交点,所以在画图像的时候,先画出函数y=ax2+bx+c,再画出直线图象,而直线与曲线的交点,便是方程的根。
用二次函数图象解一元二次方程的方法:
两个函数图象的交点坐标就是对应函数解析式所组成的方程组的解.
函数解析式对应方程的根,就是该函数图象与x轴交点的横坐标;
归纳总结
1.抛物线y=-x2+4x-4与坐标轴的交点个数为
(
)
A.0
B.1
C.2
D.3
随堂演练
C
2.二次函数y=x2-2x-3的图象如图所示,则当函数值y<0时,
x的取值范围是
(
)
A.x<-1
B.x>3
C.-1D.x<-1或x>3
C
3.在平面直角坐标系中,二次函数y1=-x2+4x和一次函数y2=2x的图象如图所示,那么不等式
-x2+4x>2x的解集是
(
)
A.x<0
B.0C.0D.2C
4.已知二次函数y=2x2-2和一次函数y=5x+1.
(1)你能用图象法求出方程2x2-2=5x+1的解吗?试试看;
(2)请通过解方程的方法验证(1)中的答案.
5.已知抛物线y=ax2+bx+c与y轴交点的纵坐标为-3,
对称轴为直线x=1且过点(-1,0).
(1)求该抛物线所对应的函数关系式;
(2)画出图象,并利用图象回答:当x为何值时,y>0?
当x为何值时,y<0?
(2)画图象略.
当x<-1或x>3时,y>0;
当-1课堂小结
二次函数y=ax2+bx+c的图象与x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式
两个交点
两个相异的实数根
b2-4ac>0
一个交点
两个相等的实数根
b2-4ac=0
没有交点
没有实数根
b2-4ac<0
图象
函数值
自变量的取值(范围)
y>0
x<x1或
x>x2
y=0
x=x1或
x=x2
y<0
x1<x<x2
y>0
x1<x<x2
y=0
x=x1或
x=x2
y<0
x<x1或
x>x2
根据图象可直观地回答使得函数值y大于、等于或小于
零时x的取值(范围),具体如下表所述:
变
形
函数图象交点的横坐标
变
形
函数图象交点的横坐标
变形方式
21.3
二次函数与一元二次方程的关系
情景导入
前面我们学习通过观察一次函数的图象,研究了一次函数与一次方程、一次不等式之间的关系。
想一想,通过一次函数的图象可以得出哪些结论?
由一次函数y=2x-3的图象可知:
它与x轴的交点坐标是(
,0
),
即当x=
时,y=0
即x=
是一元一次方程
2x-3=0的根。
当x>
时,图象在x轴上方即y>0,
所以x>
为一元一次不等式
2x-3>0的解集;
当x<
时,图象在x轴下方即y<0,
所以x<
为一元一次不等式
2x-3<0的解集.
观察下图,说一说二次函数
的图象与x轴有几个交点?交点的横坐标与一元二次方程
的根有什么关系?
观察图象可知,二次函数
的图象与x轴有两个交点。两交点分别为(-2,0)(-1,0),交点横坐标可看作是方程
的根。
根据上述问题3
画出的图象,继续回答下列问题:
(1)当x取何值时,y<0?当x取何值时,y>0?
(2)试用含有x的不等式来描述问题(1)。
通过解答以上问题,想一想,二次函数与一元二次方程与一元二次不等式有什么联系?
解:
(1)
(2)
试一试
对于一元二次方程
,
当
时有实数根,这个实数根就是对应二次函数
的值等于0时自变量x的一个值,即二次函数的图象与x轴一个交点的横坐标。
二次函数与一元二次方程是紧密联系又相互渗透的,两者经常综合命题
1.二次函数y=ax2+bx+c,当y=0(或其他数值m)时,就变
成了一元二次方程ax2+bx+c=0(或m).
2.二次函数y=ax2+bx+c的图象与轴的交点情况有三种:
有两个交点,有一个交点,没有交点.如果抛物线y=ax2
+bx+c与x轴交于两点(x1,0)
(x2,0)则x1,x2是一元二
次方程ax2+bx+c=0的两个不等实根,反之亦成立.
3.抛物线y=ax2+bx+c与x轴交于两点
一元二次方程ax2+bx+c=0有两个不相等的实数根
b2-4ac
>0;抛物线y=ax2+bx+c与x轴只有一个交点
一元二次方程ax2+bx+c=0有两个相等的实数根
b2-4ac
=0;抛物线y=ax2+bx+c与x轴没有交点
一元二次方程ax2+bx+c=0没有实数根
b2-4ac
<
0.
例题讲解
例
用图象法求一元二次方程x2+2x-1=0的近似解(精确到0.1).
由图象可知,方程有两个实数根,一个在-3和-2之间.另—个在0和1之间.
先求位于-3和-2之间的根.
x
…
-2.6
-2.5
-2.4
-2.3
…
y
…
…
0.56
0.25
-0.04
-0.31
观察x取何值时,y值最接近0?
先求位于-3和-2之间的根.
x
…
-2.6
-2.5
-2.4
-2.3
…
y
…
…
0.56
0.25
-0.04
-0.31
观察上表可以发现,当x分别取-2.5和-2.4时,对应的y由正变负,可见在-2.5与-2.4之间有一个x使y=0,即有方程
的一个根。
请同学们仿照上面的方法,求出上述方程精确到0.1的另一个根.
函数y=ax2+bx+c与直线y=kx+d的交点,所以在画图像的时候,先画出函数y=ax2+bx+c,再画出直线图象,而直线与曲线的交点,便是方程的根。
用二次函数图象解一元二次方程的方法:
两个函数图象的交点坐标就是对应函数解析式所组成的方程组的解.
函数解析式对应方程的根,就是该函数图象与x轴交点的横坐标;
归纳总结
1.抛物线y=-x2+4x-4与坐标轴的交点个数为
(
)
A.0
B.1
C.2
D.3
随堂演练
C
2.二次函数y=x2-2x-3的图象如图所示,则当函数值y<0时,
x的取值范围是
(
)
A.x<-1
B.x>3
C.-1
C
3.在平面直角坐标系中,二次函数y1=-x2+4x和一次函数y2=2x的图象如图所示,那么不等式
-x2+4x>2x的解集是
(
)
A.x<0
B.0
4.已知二次函数y=2x2-2和一次函数y=5x+1.
(1)你能用图象法求出方程2x2-2=5x+1的解吗?试试看;
(2)请通过解方程的方法验证(1)中的答案.
5.已知抛物线y=ax2+bx+c与y轴交点的纵坐标为-3,
对称轴为直线x=1且过点(-1,0).
(1)求该抛物线所对应的函数关系式;
(2)画出图象,并利用图象回答:当x为何值时,y>0?
当x为何值时,y<0?
(2)画图象略.
当x<-1或x>3时,y>0;
当-1
二次函数y=ax2+bx+c的图象与x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式
两个交点
两个相异的实数根
b2-4ac>0
一个交点
两个相等的实数根
b2-4ac=0
没有交点
没有实数根
b2-4ac<0
图象
函数值
自变量的取值(范围)
y>0
x<x1或
x>x2
y=0
x=x1或
x=x2
y<0
x1<x<x2
y>0
x1<x<x2
y=0
x=x1或
x=x2
y<0
x<x1或
x>x2
根据图象可直观地回答使得函数值y大于、等于或小于
零时x的取值(范围),具体如下表所述:
变
形
函数图象交点的横坐标
变
形
函数图象交点的横坐标
变形方式
