2020-2021学年湖南省长沙市天心区明德八年级(下)期末数学试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年湖南省长沙市天心区明德八年级(下)期末数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 895.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 07:05:51 | ||
图片预览



文档简介
2020-2021学年湖南省长沙市天心区明德八年级(下)期末数学试卷
一、选择题(每小题3分,共30分)
1.如图,下列的四个图象中,不能表示y是x的函数图象的是( )
A. B.
C. D.
2.下列运算结果正确的是( )
A. B. C. D.
3.下列各组数中,不能构成直角三角形的一组是( )
A.7,24,25 B.,4,5 C.3,4,5 D.4,5,6
4.在?ABCD中,如果∠A+∠C=140°,那么∠C的大小是( )
A.20° B.40° C.70° D.75°
5.为了向建党一百周年献礼,我市中小学生开展了图说党史比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.平均数是85 D.方差是84
6.正方形具有而矩形不具有的性质是( )
A.对角相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
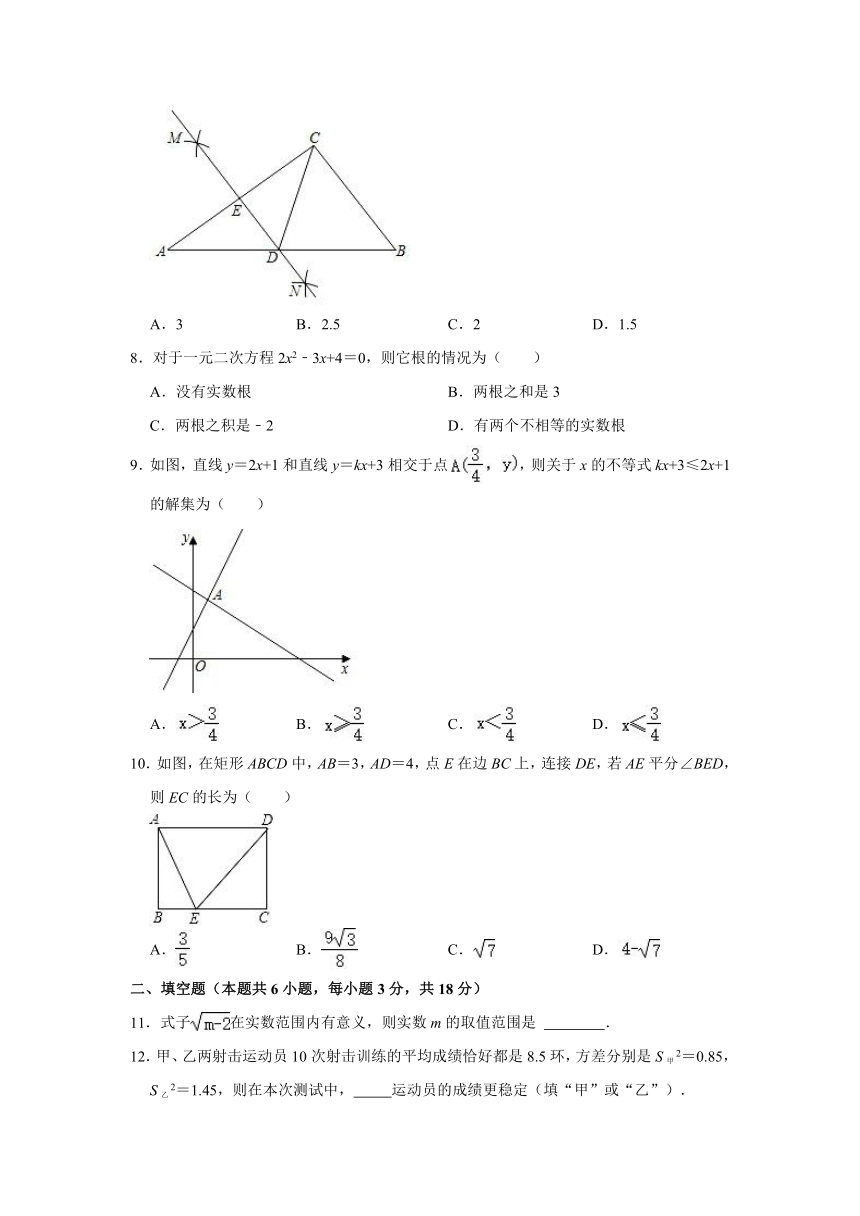
7.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,分别以点A和点C为圆心,以大于长为半径画弧,两弧交于点M和点N,作直线MN交AC于点E,交AB于点D,连接CD,则CD长为( )
A.3 B.2.5 C.2 D.1.5
8.对于一元二次方程2x2﹣3x+4=0,则它根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是﹣2 D.有两个不相等的实数根
9.如图,直线y=2x+1和直线y=kx+3相交于点,则关于x的不等式kx+3≤2x+1的解集为( )
A. B. C. D.
10.如图,在矩形ABCD中,AB=3,AD=4,点E在边BC上,连接DE,若AE平分∠BED,则EC的长为( )
A. B. C. D.
二、填空题(本题共6小题,每小题3分,共18分)
11.式子在实数范围内有意义,则实数m的取值范围是 .
12.甲、乙两射击运动员10次射击训练的平均成绩恰好都是8.5环,方差分别是S甲2=0.85,S乙2=1.45,则在本次测试中, 运动员的成绩更稳定(填“甲”或“乙”).
13.若直线y=x﹣1上有两点A(x1,﹣3)和B(x2,1),则x1 x2(填“>”或“<”).
14.已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为 .
15.如图,在菱形ABCD中,点E,F分别是边AD、BD的中点,若EF=2,则BC长为 .
16.如图,在?ABCD中,将△ABC沿着AC所在的直线翻折得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是 .
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题6分,第22,23题每小题6分,第24,25题每小题6分,共72分,解答应写出必要的文字说明或演算过程)
17.计算:.
18.在四边形ABCD中,已知AB=10,BC=6,AD=8,且AC⊥BC于点C.试求:
(1)AC的长;
(2)∠BCD的度数.
19.解一元二次方程:
(1)2x2﹣8=0;
(2)x2﹣6=2(x+1).
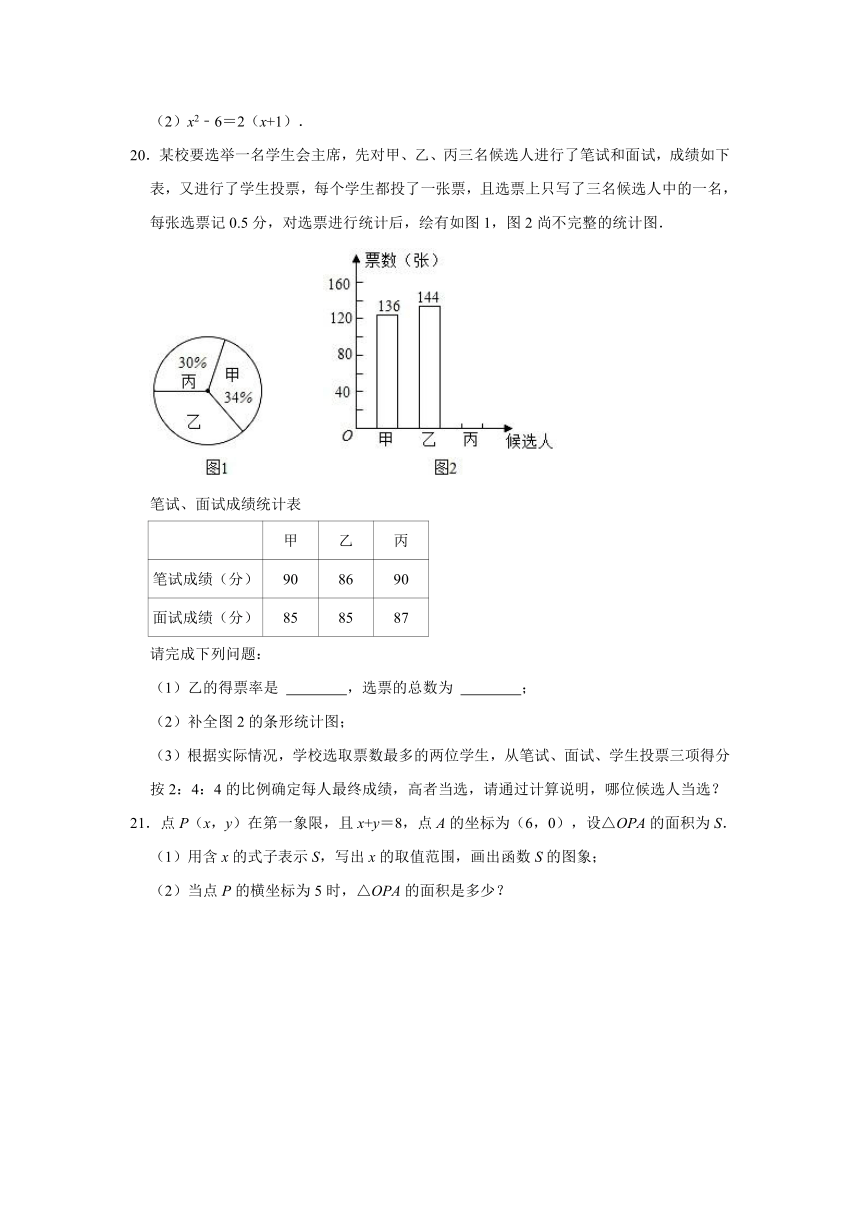
20.某校要选举一名学生会主席,先对甲、乙、丙三名候选人进行了笔试和面试,成绩如下表,又进行了学生投票,每个学生都投了一张票,且选票上只写了三名候选人中的一名,每张选票记0.5分,对选票进行统计后,绘有如图1,图2尚不完整的统计图.
笔试、面试成绩统计表
甲 乙 丙
笔试成绩(分) 90 86 90
面试成绩(分) 85 85 87
请完成下列问题:
(1)乙的得票率是 ,选票的总数为 ;
(2)补全图2的条形统计图;
(3)根据实际情况,学校选取票数最多的两位学生,从笔试、面试、学生投票三项得分按2:4:4的比例确定每人最终成绩,高者当选,请通过计算说明,哪位候选人当选?
21.点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.
(1)用含x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积是多少?
22.如图,?ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证:?ABCD是矩形;
(2)求点A到线段BD的距离.
23.为积极响应新旧功能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应是多少万元?
24.我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
25.【基础巩固】
(1)如图1,四边形ABCD的两条对角线AC,BD交于点O,若AC⊥BD,求证:AB2+CD2=AD2+BC2.
【尝试应用】
(2)如图2,在△ABC中,AB=3,BC=6,AC=4,分别以AB,AC为边向外作两个等腰直角三角形BAD和CAE,使得∠BAD=∠CAE=90°,连接DE,求DE的长.
【拓展提高】
(3)如图3,四边形ABCD是菱形,对角线AC,BD交于点O,点E,F分别是OA,OD的中点,连接BE,CF并延长交于点P.若BP2+CP2=60,求菱形的周长.
参考答案
一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项,本题共10题,每小题3分,共30分)
1.如图,下列的四个图象中,不能表示y是x的函数图象的是( )
A. B.
C. D.
解:A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故A不合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故B不合题意;
C、满足对于x的每一个取值,y都有唯一确定的值与之对应关系故C不合题意;
D、,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故D符合题意;
故选:D.
2.下列运算结果正确的是( )
A. B. C. D.
解:A.()2=3,故此选项不合题意;
B.+无法合并,故此选项不合题意;
C.÷=2,故此选项符合题意;
D.×=,故此选项不合题意.
故选:C.
3.下列各组数中,不能构成直角三角形的一组是( )
A.7,24,25 B.,4,5 C.3,4,5 D.4,5,6
解:A、72+242=252,能构成直角三角形,故此选项不符合题意;
B、42+52=()2,能构成直角三角形,故此选项不符合题意;
C、32+42=52,能构成直角三角形,故此选项不符合题意;
D、52+42≠62,不能构成直角三角形,故此选项符合题意.
故选:D.
4.在?ABCD中,如果∠A+∠C=140°,那么∠C的大小是( )
A.20° B.40° C.70° D.75°
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=140°,
∴2∠C=140°,
∴∠C=70°,
故选:C.
5.为了向建党一百周年献礼,我市中小学生开展了图说党史比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.平均数是85 D.方差是84
解:将数据重新排列为82,82,83,85,86,92,
A、数据的众数为82,此选项正确,不符合题意;
B、数据的中位数为=84,此选项正确,不符合题意;
C、数据的平均数为×(82+82+83+85+86+92)=85,此选项正确,不符合题意;
D、方差为×[(85﹣85)2+(83﹣85)2+2×(82﹣85)2+(86﹣85)2+(92﹣85)2]=12,此选项错误,符合题意;
故选:D.
6.正方形具有而矩形不具有的性质是( )
A.对角相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
解:因为正方形的对角相等,对角线相等、垂直、且互相平分,矩形的对角相等,对角线相等,互相平分,
所以正方形具有而矩形不具有的性质是对角线互相垂直.
故选:D.
7.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,分别以点A和点C为圆心,以大于长为半径画弧,两弧交于点M和点N,作直线MN交AC于点E,交AB于点D,连接CD,则CD长为( )
A.3 B.2.5 C.2 D.1.5
解:由作图可知,DE垂直平分线段AC,
∴DE⊥AC,AE=EC,
∵∠AED=∠ACB=90°,
∴DE∥BC,
∴AD=DB,
∵AC=4,BC=3,
∴AB===5,
∴CD=AB=2.5,
故选:B.
8.对于一元二次方程2x2﹣3x+4=0,则它根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是﹣2 D.有两个不相等的实数根
解:∵a=2,b=﹣3,c=4,
∴△=b2﹣4ac=(﹣3)2﹣4×2×4=﹣23<0,
∴一元二次方程2x2﹣3x+4=0没有实数根.
故选:A.
9.如图,直线y=2x+1和直线y=kx+3相交于点,则关于x的不等式kx+3≤2x+1的解集为( )
A. B. C. D.
解:由函数图象可知,当x≥时,直线y=2x+1的图象不在直线y=kx+3的图象的下方,
∵当x≥时,kx+3≤2x+1,
故选:B.
10.如图,在矩形ABCD中,AB=3,AD=4,点E在边BC上,连接DE,若AE平分∠BED,则EC的长为( )
A. B. C. D.
解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD=3,
∴∠DAE=∠AEB,
∵AE平分∠BED,
∴∠AED=∠AEB,
∴∠AED=∠DAE,
∴AD=DE=4,
∴EC===,
故选:C.
二、填空题(本题共6小题,每小题3分,共18分)
11.式子在实数范围内有意义,则实数m的取值范围是 m≥2 .
解:式子在实数范围内有意义,
则m﹣2≥0,
解得:m≥2.
故答案为:m≥2.
12.甲、乙两射击运动员10次射击训练的平均成绩恰好都是8.5环,方差分别是S甲2=0.85,S乙2=1.45,则在本次测试中, 甲 运动员的成绩更稳定(填“甲”或“乙”).
解:∵S甲2=0.85,S乙2=1.45,
∴S2甲<S2乙,
∴甲运动员比乙运动员的成绩稳定;
故答案为:甲.
13.若直线y=x﹣1上有两点A(x1,﹣3)和B(x2,1),则x1 < x2(填“>”或“<”).
解:∵直线y=x﹣1上有两点A(x1,﹣3)和B(x2,1),
∴﹣3=x1﹣1,1=x2﹣1.
∴x1=﹣2,x2=2,
∴x1<x2.
故答案为:<.
14.已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为 ﹣1 .
解:设方程的两个根为a、b,
∴a+b=﹣3,
∵方程的一根a=﹣2,
∴b=﹣1.
故答案为:﹣1.
15.如图,在菱形ABCD中,点E,F分别是边AD、BD的中点,若EF=2,则BC长为 4 .
解:∵点E,F分别是边AD、BD的中点,
∴AB=2EF=4,
∵四边形ABCD是菱形,
∴AB=BC=4,
故答案为:4.
16.如图,在?ABCD中,将△ABC沿着AC所在的直线翻折得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是 .
解:∵将△ABC沿着AC所在的直线翻折得到△AB′C,
∴△ABC≌△AB'C,
∴AB=AB',∠B=∠AB'C,∠ACB=∠ACB'
∵∠B=60°,∠ACB=45°,
∴∠ACB'=45°,
∴∠BCB'=90°,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴△EAC为等腰直角三角形,
∵AC=,
∴AE=EC=,
∵平行四边形ABCD,
∴∠ADC=∠B=60°,
在Rt△CDE中,ED=1,CD=2,
∴AB=AB'=2,
在Rt△AEB'中,B'E=1,
在Rt△EDB'中,B'D=,
故答案为.
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题6分,第22,23题每小题6分,第24,25题每小题6分,共72分,解答应写出必要的文字说明或演算过程)
17.计算:.
解:原式=3+2﹣2+1
=4.
18.在四边形ABCD中,已知AB=10,BC=6,AD=8,且AC⊥BC于点C.试求:
(1)AC的长;
(2)∠BCD的度数.
解:(1)∵AB=10,BC=6,AC⊥BC,
∴AC=8;
(2)∵AD=8,AC=8,CD=8,
∴CD2=AD2+AC2,
∴∠CAD=90°,
又∵AD=AC=8,
∴∠ACD=∠ADC=45°,
∴∠BCD=90°+45°=135°.
19.解一元二次方程:
(1)2x2﹣8=0;
(2)x2﹣6=2(x+1).
解:(1)∵x2=4,
∴x=±2,
∴x1=2,x2=﹣2;
(2)方程整理为x2﹣2x﹣8.
(x﹣4)(x+2)=0,
x﹣4=0或x+2=0,
∴x1=4,x2=﹣2.
20.某校要选举一名学生会主席,先对甲、乙、丙三名候选人进行了笔试和面试,成绩如下表,又进行了学生投票,每个学生都投了一张票,且选票上只写了三名候选人中的一名,每张选票记0.5分,对选票进行统计后,绘有如图1,图2尚不完整的统计图.
笔试、面试成绩统计表
甲 乙 丙
笔试成绩(分) 90 86 90
面试成绩(分) 85 85 87
请完成下列问题:
(1)乙的得票率是 36% ,选票的总数为 400 ;
(2)补全图2的条形统计图;
(3)根据实际情况,学校选取票数最多的两位学生,从笔试、面试、学生投票三项得分按2:4:4的比例确定每人最终成绩,高者当选,请通过计算说明,哪位候选人当选?
解:(1)1﹣30%﹣34%=36% 136÷34%=400.
故答案为:36%,400;
(2)400×30%=120(人),补图如下:
(3)将笔试、面试、学生投票三项得分按2:4:4的比例确定每人的最终成绩为:
甲的成绩:90×0.2+85×0.4+136×0.5×0.4=79.2(分),
乙的成绩:86×0.2+85×0.4+144×0.5×0.4=80(分),
丙的成绩:90×0.2+87×0.4+120×0.5×0.4=76.8(分),
∵80>79.2>76.8,
∴乙当选.
21.点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.
(1)用含x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积是多少?
解:(1)∵A和P点的坐标分别是(6,0)、(x,y),
∴△OPA的面积=OA?|yP|,
∴S=×6×|y|=3y.
∵x+y=8,
∴y=8﹣x.
∴S=3(8﹣x)=24﹣3x;
∵S=﹣3x+24>0,
解得:x<8;
又∵点P在第一象限,
∴x>0,
即x的范围为:0<x<8;
∵S=﹣3x+24,S是x的一次函数,
∴函数图象经过点(8,0),(0,24).
所画图象如下:
(2)∵S=﹣3x+24,
∴当x=5时,S=﹣3×5+24=9.
即当点P的横坐标为5时,△OPA的面积为9.
22.如图,?ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证:?ABCD是矩形;
(2)求点A到线段BD的距离.
【解答】(1)证明:∵△AOB为等边三角形,
∴∠BAO=∠AOB=60°,OA=OB,
∵四边形ABCD是平行四边形
∴OB=OD=BD,OA=OC=AC,
∴BD=AC,
∴?ABCD是矩形;
(2)解:∵?ABCD是矩形,
∴∠BAD=90°,
∵∠ABO=60°,
∴∠ADB=90°﹣60°=30°,
∴AD=AB=4,
设点A到线段BD的距离为h,
∵S△ABD=BD?h=AB?AD,
∴8h=4×4,
∴h=2,
即点A到线段BD的距离为2.
23.为积极响应新旧功能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应是多少万元?
解:(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),
将(35,550)、(40,500)代入y=kx+b,得
.
解得:,
∴年销售量y与销售单价x的函数关系式为y=﹣10x+900;
(2)设此设备的销售单价为x万元/台,
则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+900)台,
根据题意得:(x﹣30)(﹣10x+900)=8000.
整理,得:x2﹣120x+3500=0,
解得:x1=50,x2=70.
∵此设备的销售单价不得高于60万元,
∴x=50.
答:该设备的销售单价应是50万元/台.
24.我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
【解答】(1)解:根据互为“M”函数的定义,
∴函数y=2x+5的“M”函数为y=﹣2x+5;
(2)解:根据题意,y=mx+n 和 y=﹣mx+n 为一对“M函数”.
∴AB=AC,
又∵∠BAC=90°,
∴△ABC 为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵OB=OC,
∴∠BAO=∠CAO=45°,
∴OA=OB=OC,
又∵ 且 BC=2AO,
∴,
∵A、B、C是一次函数y=mx+n与y=﹣mx+n(m≠0)的图象于坐标轴的交点,
∴A(0,n),B(﹣,0),C(,0),
∵OA=OB=n,
∴=2,
∴m=1,
∴ 和 ;
(3)解:根据等腰三角形的性质,分情况,
∵,
∴AB=4,
由(2)知,A(0,2),B(﹣2,0),C(2,0),
∴①以 A 为顶点,则 AB=AD,
当点D在点A上方时,AD=2+4,
当点D在点A下方时,AD=2﹣4,
∴D1(0,2+4),D2(0,2﹣4),
②以 B 为顶点,则 BA=BD,
此时点D在y轴负半轴,
∴D3(0,﹣2),
③以 D 为顶点,则 DA=DB,
此时D为坐标原点,
∴D4(0,0).
∴D点坐标为 D1(0,2+4),D2(0,2﹣4),D3(0,﹣2),∴D4(0,0).
25.【基础巩固】
(1)如图1,四边形ABCD的两条对角线AC,BD交于点O,若AC⊥BD,求证:AB2+CD2=AD2+BC2.
【尝试应用】
(2)如图2,在△ABC中,AB=3,BC=6,AC=4,分别以AB,AC为边向外作两个等腰直角三角形BAD和CAE,使得∠BAD=∠CAE=90°,连接DE,求DE的长.
【拓展提高】
(3)如图3,四边形ABCD是菱形,对角线AC,BD交于点O,点E,F分别是OA,OD的中点,连接BE,CF并延长交于点P.若BP2+CP2=60,求菱形的周长.
【解答】(1)证明:∵AC⊥BD,
∴∠AOB=∠BOC=∠COD=∠AOD=90°,
∴OA2+OB2=AB2,OB2+OC2=BC2,OC2+OD2=CD2,OD2+OA2=AD2,
∴AB2+CD2=OA2+OB2+OC2+OD2,AD2+BC2=OD2+OA2+OB2+OC2,
∴AB2+CD2=AD2+BC2.
(2)解:连接CD、BE交于点F,BE交AD于G,如图2所示:
∵△BAD和△CAE是等腰直角三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=90°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC,
∴△BAE≌△DAC(SAS),
∴∠ABE=∠ADC,
∵∠ABE+∠AGB=90°,∠DGF=∠AGB,
∴∠ADC+∠DGF=90°,
∴∠BFD=90°,
∴BE⊥CD,
由(1)得:BD2+CE2=BC2+DE2,
在Rt△ABD中,AD=AB=3,
∴BD=AB=3,
在Rt△ACE中,AE=AC=4,
∴CE=AC=4,
∴(3)2+(4)2=62+DE2,
解得:DE=;
(3)解:连接EF,如图3所示:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,AD∥BC,
∵点E,F分别是OA,OD的中点,
∴EF是△AOD的中位线,
∴EF∥AD∥BC,EF=AD=BC,
∴EF是△BCP的中位线,
∴EP=BE=BP,CF=FP=CP,
在四边形BCFE中,CE⊥BF,
∴BE2+CF2=BC2+EF2,
即(BP)2+(CP)2=BC2+(BC)2,
∴(BP2+CP2)=BC2,
∵BP2+CP2=60,
∴×60=BC2,
∴BC==2,
∴菱形的周长=4BC=8.
一、选择题(每小题3分,共30分)
1.如图,下列的四个图象中,不能表示y是x的函数图象的是( )
A. B.
C. D.
2.下列运算结果正确的是( )
A. B. C. D.
3.下列各组数中,不能构成直角三角形的一组是( )
A.7,24,25 B.,4,5 C.3,4,5 D.4,5,6
4.在?ABCD中,如果∠A+∠C=140°,那么∠C的大小是( )
A.20° B.40° C.70° D.75°
5.为了向建党一百周年献礼,我市中小学生开展了图说党史比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.平均数是85 D.方差是84
6.正方形具有而矩形不具有的性质是( )
A.对角相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
7.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,分别以点A和点C为圆心,以大于长为半径画弧,两弧交于点M和点N,作直线MN交AC于点E,交AB于点D,连接CD,则CD长为( )
A.3 B.2.5 C.2 D.1.5
8.对于一元二次方程2x2﹣3x+4=0,则它根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是﹣2 D.有两个不相等的实数根
9.如图,直线y=2x+1和直线y=kx+3相交于点,则关于x的不等式kx+3≤2x+1的解集为( )
A. B. C. D.
10.如图,在矩形ABCD中,AB=3,AD=4,点E在边BC上,连接DE,若AE平分∠BED,则EC的长为( )
A. B. C. D.
二、填空题(本题共6小题,每小题3分,共18分)
11.式子在实数范围内有意义,则实数m的取值范围是 .
12.甲、乙两射击运动员10次射击训练的平均成绩恰好都是8.5环,方差分别是S甲2=0.85,S乙2=1.45,则在本次测试中, 运动员的成绩更稳定(填“甲”或“乙”).
13.若直线y=x﹣1上有两点A(x1,﹣3)和B(x2,1),则x1 x2(填“>”或“<”).
14.已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为 .
15.如图,在菱形ABCD中,点E,F分别是边AD、BD的中点,若EF=2,则BC长为 .
16.如图,在?ABCD中,将△ABC沿着AC所在的直线翻折得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是 .
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题6分,第22,23题每小题6分,第24,25题每小题6分,共72分,解答应写出必要的文字说明或演算过程)
17.计算:.
18.在四边形ABCD中,已知AB=10,BC=6,AD=8,且AC⊥BC于点C.试求:
(1)AC的长;
(2)∠BCD的度数.
19.解一元二次方程:
(1)2x2﹣8=0;
(2)x2﹣6=2(x+1).
20.某校要选举一名学生会主席,先对甲、乙、丙三名候选人进行了笔试和面试,成绩如下表,又进行了学生投票,每个学生都投了一张票,且选票上只写了三名候选人中的一名,每张选票记0.5分,对选票进行统计后,绘有如图1,图2尚不完整的统计图.
笔试、面试成绩统计表
甲 乙 丙
笔试成绩(分) 90 86 90
面试成绩(分) 85 85 87
请完成下列问题:
(1)乙的得票率是 ,选票的总数为 ;
(2)补全图2的条形统计图;
(3)根据实际情况,学校选取票数最多的两位学生,从笔试、面试、学生投票三项得分按2:4:4的比例确定每人最终成绩,高者当选,请通过计算说明,哪位候选人当选?
21.点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.
(1)用含x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积是多少?
22.如图,?ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证:?ABCD是矩形;
(2)求点A到线段BD的距离.
23.为积极响应新旧功能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应是多少万元?
24.我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
25.【基础巩固】
(1)如图1,四边形ABCD的两条对角线AC,BD交于点O,若AC⊥BD,求证:AB2+CD2=AD2+BC2.
【尝试应用】
(2)如图2,在△ABC中,AB=3,BC=6,AC=4,分别以AB,AC为边向外作两个等腰直角三角形BAD和CAE,使得∠BAD=∠CAE=90°,连接DE,求DE的长.
【拓展提高】
(3)如图3,四边形ABCD是菱形,对角线AC,BD交于点O,点E,F分别是OA,OD的中点,连接BE,CF并延长交于点P.若BP2+CP2=60,求菱形的周长.
参考答案
一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项,本题共10题,每小题3分,共30分)
1.如图,下列的四个图象中,不能表示y是x的函数图象的是( )
A. B.
C. D.
解:A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故A不合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故B不合题意;
C、满足对于x的每一个取值,y都有唯一确定的值与之对应关系故C不合题意;
D、,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故D符合题意;
故选:D.
2.下列运算结果正确的是( )
A. B. C. D.
解:A.()2=3,故此选项不合题意;
B.+无法合并,故此选项不合题意;
C.÷=2,故此选项符合题意;
D.×=,故此选项不合题意.
故选:C.
3.下列各组数中,不能构成直角三角形的一组是( )
A.7,24,25 B.,4,5 C.3,4,5 D.4,5,6
解:A、72+242=252,能构成直角三角形,故此选项不符合题意;
B、42+52=()2,能构成直角三角形,故此选项不符合题意;
C、32+42=52,能构成直角三角形,故此选项不符合题意;
D、52+42≠62,不能构成直角三角形,故此选项符合题意.
故选:D.
4.在?ABCD中,如果∠A+∠C=140°,那么∠C的大小是( )
A.20° B.40° C.70° D.75°
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=140°,
∴2∠C=140°,
∴∠C=70°,
故选:C.
5.为了向建党一百周年献礼,我市中小学生开展了图说党史比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.平均数是85 D.方差是84
解:将数据重新排列为82,82,83,85,86,92,
A、数据的众数为82,此选项正确,不符合题意;
B、数据的中位数为=84,此选项正确,不符合题意;
C、数据的平均数为×(82+82+83+85+86+92)=85,此选项正确,不符合题意;
D、方差为×[(85﹣85)2+(83﹣85)2+2×(82﹣85)2+(86﹣85)2+(92﹣85)2]=12,此选项错误,符合题意;
故选:D.
6.正方形具有而矩形不具有的性质是( )
A.对角相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
解:因为正方形的对角相等,对角线相等、垂直、且互相平分,矩形的对角相等,对角线相等,互相平分,
所以正方形具有而矩形不具有的性质是对角线互相垂直.
故选:D.
7.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,分别以点A和点C为圆心,以大于长为半径画弧,两弧交于点M和点N,作直线MN交AC于点E,交AB于点D,连接CD,则CD长为( )
A.3 B.2.5 C.2 D.1.5
解:由作图可知,DE垂直平分线段AC,
∴DE⊥AC,AE=EC,
∵∠AED=∠ACB=90°,
∴DE∥BC,
∴AD=DB,
∵AC=4,BC=3,
∴AB===5,
∴CD=AB=2.5,
故选:B.
8.对于一元二次方程2x2﹣3x+4=0,则它根的情况为( )
A.没有实数根 B.两根之和是3
C.两根之积是﹣2 D.有两个不相等的实数根
解:∵a=2,b=﹣3,c=4,
∴△=b2﹣4ac=(﹣3)2﹣4×2×4=﹣23<0,
∴一元二次方程2x2﹣3x+4=0没有实数根.
故选:A.
9.如图,直线y=2x+1和直线y=kx+3相交于点,则关于x的不等式kx+3≤2x+1的解集为( )
A. B. C. D.
解:由函数图象可知,当x≥时,直线y=2x+1的图象不在直线y=kx+3的图象的下方,
∵当x≥时,kx+3≤2x+1,
故选:B.
10.如图,在矩形ABCD中,AB=3,AD=4,点E在边BC上,连接DE,若AE平分∠BED,则EC的长为( )
A. B. C. D.
解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD=3,
∴∠DAE=∠AEB,
∵AE平分∠BED,
∴∠AED=∠AEB,
∴∠AED=∠DAE,
∴AD=DE=4,
∴EC===,
故选:C.
二、填空题(本题共6小题,每小题3分,共18分)
11.式子在实数范围内有意义,则实数m的取值范围是 m≥2 .
解:式子在实数范围内有意义,
则m﹣2≥0,
解得:m≥2.
故答案为:m≥2.
12.甲、乙两射击运动员10次射击训练的平均成绩恰好都是8.5环,方差分别是S甲2=0.85,S乙2=1.45,则在本次测试中, 甲 运动员的成绩更稳定(填“甲”或“乙”).
解:∵S甲2=0.85,S乙2=1.45,
∴S2甲<S2乙,
∴甲运动员比乙运动员的成绩稳定;
故答案为:甲.
13.若直线y=x﹣1上有两点A(x1,﹣3)和B(x2,1),则x1 < x2(填“>”或“<”).
解:∵直线y=x﹣1上有两点A(x1,﹣3)和B(x2,1),
∴﹣3=x1﹣1,1=x2﹣1.
∴x1=﹣2,x2=2,
∴x1<x2.
故答案为:<.
14.已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为 ﹣1 .
解:设方程的两个根为a、b,
∴a+b=﹣3,
∵方程的一根a=﹣2,
∴b=﹣1.
故答案为:﹣1.
15.如图,在菱形ABCD中,点E,F分别是边AD、BD的中点,若EF=2,则BC长为 4 .
解:∵点E,F分别是边AD、BD的中点,
∴AB=2EF=4,
∵四边形ABCD是菱形,
∴AB=BC=4,
故答案为:4.
16.如图,在?ABCD中,将△ABC沿着AC所在的直线翻折得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是 .
解:∵将△ABC沿着AC所在的直线翻折得到△AB′C,
∴△ABC≌△AB'C,
∴AB=AB',∠B=∠AB'C,∠ACB=∠ACB'
∵∠B=60°,∠ACB=45°,
∴∠ACB'=45°,
∴∠BCB'=90°,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴△EAC为等腰直角三角形,
∵AC=,
∴AE=EC=,
∵平行四边形ABCD,
∴∠ADC=∠B=60°,
在Rt△CDE中,ED=1,CD=2,
∴AB=AB'=2,
在Rt△AEB'中,B'E=1,
在Rt△EDB'中,B'D=,
故答案为.
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题6分,第22,23题每小题6分,第24,25题每小题6分,共72分,解答应写出必要的文字说明或演算过程)
17.计算:.
解:原式=3+2﹣2+1
=4.
18.在四边形ABCD中,已知AB=10,BC=6,AD=8,且AC⊥BC于点C.试求:
(1)AC的长;
(2)∠BCD的度数.
解:(1)∵AB=10,BC=6,AC⊥BC,
∴AC=8;
(2)∵AD=8,AC=8,CD=8,
∴CD2=AD2+AC2,
∴∠CAD=90°,
又∵AD=AC=8,
∴∠ACD=∠ADC=45°,
∴∠BCD=90°+45°=135°.
19.解一元二次方程:
(1)2x2﹣8=0;
(2)x2﹣6=2(x+1).
解:(1)∵x2=4,
∴x=±2,
∴x1=2,x2=﹣2;
(2)方程整理为x2﹣2x﹣8.
(x﹣4)(x+2)=0,
x﹣4=0或x+2=0,
∴x1=4,x2=﹣2.
20.某校要选举一名学生会主席,先对甲、乙、丙三名候选人进行了笔试和面试,成绩如下表,又进行了学生投票,每个学生都投了一张票,且选票上只写了三名候选人中的一名,每张选票记0.5分,对选票进行统计后,绘有如图1,图2尚不完整的统计图.
笔试、面试成绩统计表
甲 乙 丙
笔试成绩(分) 90 86 90
面试成绩(分) 85 85 87
请完成下列问题:
(1)乙的得票率是 36% ,选票的总数为 400 ;
(2)补全图2的条形统计图;
(3)根据实际情况,学校选取票数最多的两位学生,从笔试、面试、学生投票三项得分按2:4:4的比例确定每人最终成绩,高者当选,请通过计算说明,哪位候选人当选?
解:(1)1﹣30%﹣34%=36% 136÷34%=400.
故答案为:36%,400;
(2)400×30%=120(人),补图如下:
(3)将笔试、面试、学生投票三项得分按2:4:4的比例确定每人的最终成绩为:
甲的成绩:90×0.2+85×0.4+136×0.5×0.4=79.2(分),
乙的成绩:86×0.2+85×0.4+144×0.5×0.4=80(分),
丙的成绩:90×0.2+87×0.4+120×0.5×0.4=76.8(分),
∵80>79.2>76.8,
∴乙当选.
21.点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0),设△OPA的面积为S.
(1)用含x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积是多少?
解:(1)∵A和P点的坐标分别是(6,0)、(x,y),
∴△OPA的面积=OA?|yP|,
∴S=×6×|y|=3y.
∵x+y=8,
∴y=8﹣x.
∴S=3(8﹣x)=24﹣3x;
∵S=﹣3x+24>0,
解得:x<8;
又∵点P在第一象限,
∴x>0,
即x的范围为:0<x<8;
∵S=﹣3x+24,S是x的一次函数,
∴函数图象经过点(8,0),(0,24).
所画图象如下:
(2)∵S=﹣3x+24,
∴当x=5时,S=﹣3×5+24=9.
即当点P的横坐标为5时,△OPA的面积为9.
22.如图,?ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证:?ABCD是矩形;
(2)求点A到线段BD的距离.
【解答】(1)证明:∵△AOB为等边三角形,
∴∠BAO=∠AOB=60°,OA=OB,
∵四边形ABCD是平行四边形
∴OB=OD=BD,OA=OC=AC,
∴BD=AC,
∴?ABCD是矩形;
(2)解:∵?ABCD是矩形,
∴∠BAD=90°,
∵∠ABO=60°,
∴∠ADB=90°﹣60°=30°,
∴AD=AB=4,
设点A到线段BD的距离为h,
∵S△ABD=BD?h=AB?AD,
∴8h=4×4,
∴h=2,
即点A到线段BD的距离为2.
23.为积极响应新旧功能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应是多少万元?
解:(1)设年销售量y与销售单价x的函数关系式为y=kx+b(k≠0),
将(35,550)、(40,500)代入y=kx+b,得
.
解得:,
∴年销售量y与销售单价x的函数关系式为y=﹣10x+900;
(2)设此设备的销售单价为x万元/台,
则每台设备的利润为(x﹣30)万元,销售数量为(﹣10x+900)台,
根据题意得:(x﹣30)(﹣10x+900)=8000.
整理,得:x2﹣120x+3500=0,
解得:x1=50,x2=70.
∵此设备的销售单价不得高于60万元,
∴x=50.
答:该设备的销售单价应是50万元/台.
24.我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
【解答】(1)解:根据互为“M”函数的定义,
∴函数y=2x+5的“M”函数为y=﹣2x+5;
(2)解:根据题意,y=mx+n 和 y=﹣mx+n 为一对“M函数”.
∴AB=AC,
又∵∠BAC=90°,
∴△ABC 为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵OB=OC,
∴∠BAO=∠CAO=45°,
∴OA=OB=OC,
又∵ 且 BC=2AO,
∴,
∵A、B、C是一次函数y=mx+n与y=﹣mx+n(m≠0)的图象于坐标轴的交点,
∴A(0,n),B(﹣,0),C(,0),
∵OA=OB=n,
∴=2,
∴m=1,
∴ 和 ;
(3)解:根据等腰三角形的性质,分情况,
∵,
∴AB=4,
由(2)知,A(0,2),B(﹣2,0),C(2,0),
∴①以 A 为顶点,则 AB=AD,
当点D在点A上方时,AD=2+4,
当点D在点A下方时,AD=2﹣4,
∴D1(0,2+4),D2(0,2﹣4),
②以 B 为顶点,则 BA=BD,
此时点D在y轴负半轴,
∴D3(0,﹣2),
③以 D 为顶点,则 DA=DB,
此时D为坐标原点,
∴D4(0,0).
∴D点坐标为 D1(0,2+4),D2(0,2﹣4),D3(0,﹣2),∴D4(0,0).
25.【基础巩固】
(1)如图1,四边形ABCD的两条对角线AC,BD交于点O,若AC⊥BD,求证:AB2+CD2=AD2+BC2.
【尝试应用】
(2)如图2,在△ABC中,AB=3,BC=6,AC=4,分别以AB,AC为边向外作两个等腰直角三角形BAD和CAE,使得∠BAD=∠CAE=90°,连接DE,求DE的长.
【拓展提高】
(3)如图3,四边形ABCD是菱形,对角线AC,BD交于点O,点E,F分别是OA,OD的中点,连接BE,CF并延长交于点P.若BP2+CP2=60,求菱形的周长.
【解答】(1)证明:∵AC⊥BD,
∴∠AOB=∠BOC=∠COD=∠AOD=90°,
∴OA2+OB2=AB2,OB2+OC2=BC2,OC2+OD2=CD2,OD2+OA2=AD2,
∴AB2+CD2=OA2+OB2+OC2+OD2,AD2+BC2=OD2+OA2+OB2+OC2,
∴AB2+CD2=AD2+BC2.
(2)解:连接CD、BE交于点F,BE交AD于G,如图2所示:
∵△BAD和△CAE是等腰直角三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=90°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC,
∴△BAE≌△DAC(SAS),
∴∠ABE=∠ADC,
∵∠ABE+∠AGB=90°,∠DGF=∠AGB,
∴∠ADC+∠DGF=90°,
∴∠BFD=90°,
∴BE⊥CD,
由(1)得:BD2+CE2=BC2+DE2,
在Rt△ABD中,AD=AB=3,
∴BD=AB=3,
在Rt△ACE中,AE=AC=4,
∴CE=AC=4,
∴(3)2+(4)2=62+DE2,
解得:DE=;
(3)解:连接EF,如图3所示:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,AD∥BC,
∵点E,F分别是OA,OD的中点,
∴EF是△AOD的中位线,
∴EF∥AD∥BC,EF=AD=BC,
∴EF是△BCP的中位线,
∴EP=BE=BP,CF=FP=CP,
在四边形BCFE中,CE⊥BF,
∴BE2+CF2=BC2+EF2,
即(BP)2+(CP)2=BC2+(BC)2,
∴(BP2+CP2)=BC2,
∵BP2+CP2=60,
∴×60=BC2,
∴BC==2,
∴菱形的周长=4BC=8.
同课章节目录
