2020-2021学年湖南省长沙市湘一部分学校联考八年级(下)期末数学试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年湖南省长沙市湘一部分学校联考八年级(下)期末数学试卷(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 899.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览



文档简介
2020-2021学年湖南省长沙市部分学校联考八年级(下)期末数学试卷
一、选择题(每题3分).
1.下列“表情图”中,属于轴对称图形的是( )
A. B.
C. D.
2.我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )
A.0.3×106 B.3×107 C.3×106 D.30×105
3.下列四组线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
4.下列各式中属于最简二次根式的是( )
A. B. C. D.
5.若点A(2,m)在正比例函数y=x的图象上,则m的值是( )
A. B.﹣ C.1 D.﹣1
6.下列计算正确的是( )
A.a2+a2=a4 B.2a2﹣a2=2 C.(a2)3=a5 D.a5?a2=a7
7.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
8.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.一组对边平行且对角线相等的四边形是矩形
D.四条边都相等的四边形是菱形
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
10.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x>4时,y1<y2;④b<0.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共6题)
11.直线y=﹣x+1向上平移5个单位后,得到的直线的解析式是 .
12.若在实数范围内有意义,则x的取值范围为 .
13.数据1,2,3,0,﹣3,﹣2,﹣1的中位数是 .
14.在新年晚会的投飞镖游戏环节中,5名同学的投掷成绩(单位:环)分别是:7,8,7,10,8,则这组数据的方差是 .
15.在直角三角形中,若两条直角边长分别为6cm和8cm,则斜边上的中线为 cm.
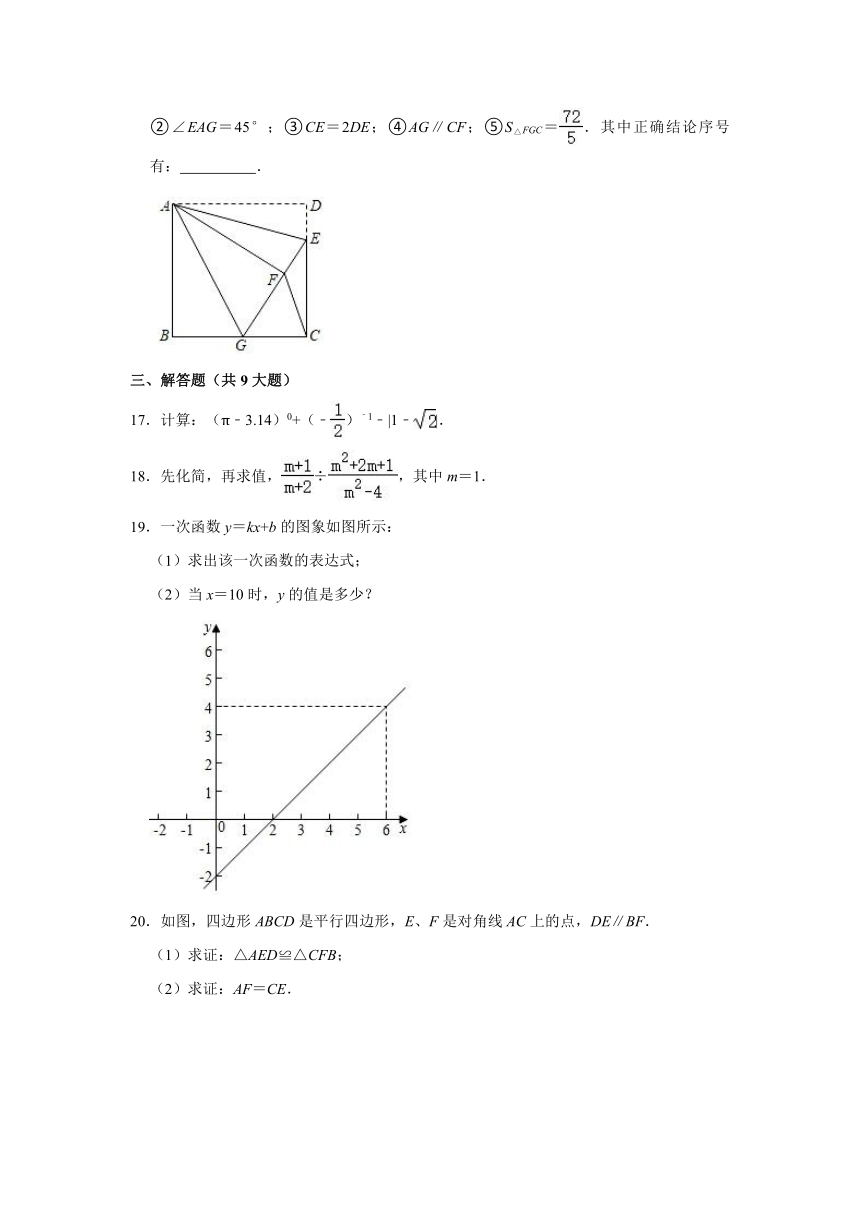
16.如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC=.其中正确结论序号有: .
三、解答题(共9大题)
17.计算:(π﹣3.14)0+(﹣)﹣1﹣|1﹣|.
18.先化简,再求值,÷,其中m=1.
19.一次函数y=kx+b的图象如图所示:
(1)求出该一次函数的表达式;
(2)当x=10时,y的值是多少?
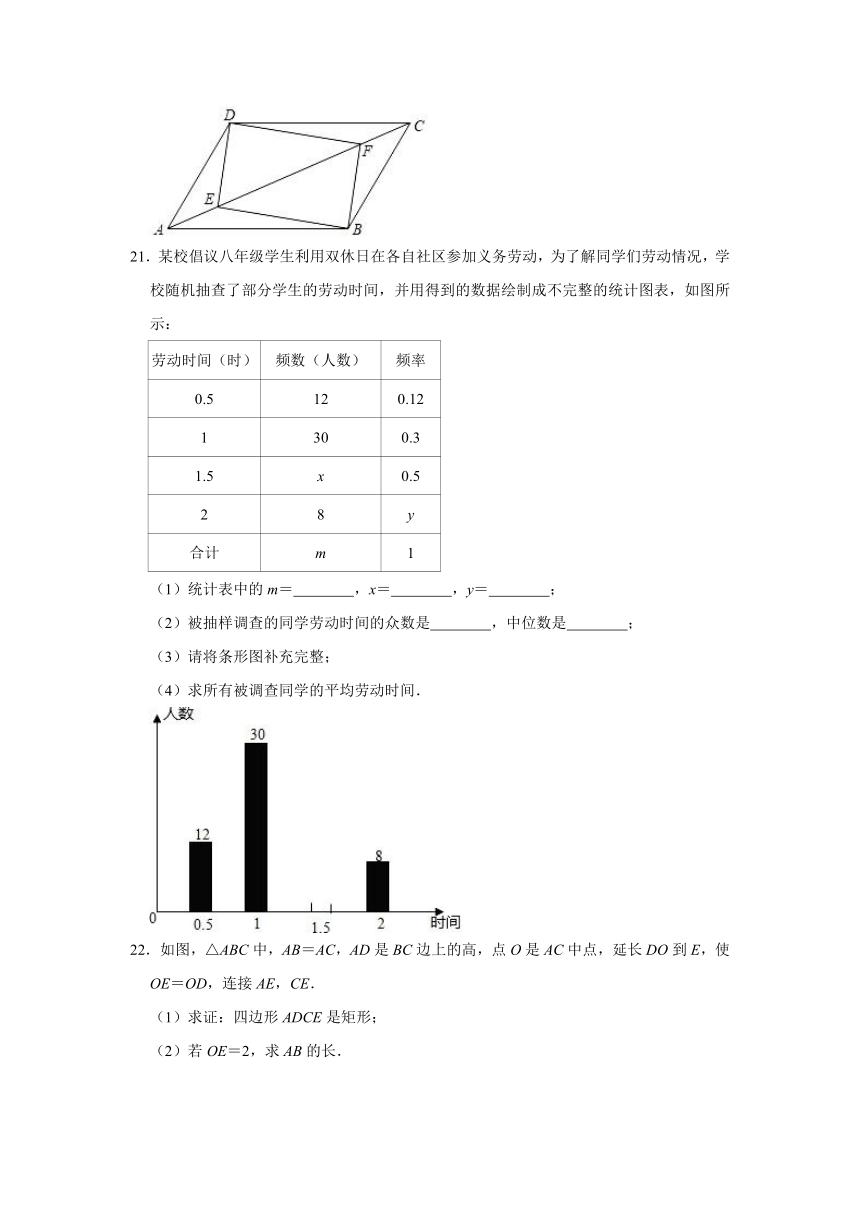
20.如图,四边形ABCD是平行四边形,E、F是对角线AC上的点,DE∥BF.
(1)求证:△AED≌△CFB;
(2)求证:AF=CE.
21.某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) 频数(人数) 频率
0.5 12 0.12
1 30 0.3
1.5 x 0.5
2 8 y
合计 m 1
(1)统计表中的m= ,x= ,y= ;
(2)被抽样调查的同学劳动时间的众数是 ,中位数是 ;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
22.如图,△ABC中,AB=AC,AD是BC边上的高,点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE是矩形;
(2)若OE=2,求AB的长.
23.将220吨物资从A地运往甲、乙两地,用大、小两种货车共18辆,恰好一次性运完这批物资,已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
甲地(元/辆) 乙地(元/辆)
大货车 700 800
小货车 400 600
(1)这两种货车各需多少辆?
(2)如果安排8辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,请写出运费W(元)与a的函数关系式.若运往甲地的物资不少于110吨,请设计出货车调配方案,并求出最少运费.
24.对于平面直角坐标系xOy中的点P(x,y),若x,y满足|y﹣x|=1,则点P(x,y)就称为“完美点”.例如:(5,6),因为|6﹣5|=1,所以(5,6)是“完美点”.
(1)点M(3,2) “完美点”;点N(﹣2,3) “完美点”(填“是”或“不是”);
(2)已知一次函数y=3x+m(m为常数)图象上有一个“完美点”的坐标是(1,2),一次函数y=3x+m(m为常数)图象上是否存在其他“完美点”?若存在,请求出来;若不存在,请说明理由.
(3)点A和点B为一次函数y=2x+a(a为常数且a<﹣2)图象上的两个“完美点”,点Q在x轴上运动,当QA+QB最小时,求点Q的坐标(用含字母a的式子表示).
25.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共10题)
1.下列“表情图”中,属于轴对称图形的是( )
A. B.
C. D.
解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确;
故选:D.
2.我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )
A.0.3×106 B.3×107 C.3×106 D.30×105
解:3000000=3×106,
故选:C.
3.下列四组线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
解:A、12+22≠32,不能构成直角三角形,故不符合题意;
B、22+32≠42,不能构成直角三角形,故不符合题意;
C、32+42=52,能构成直角三角形,故符合题意;
D、42+52≠62,不能构成直角三角形,故不符合题意.
故选:C.
4.下列各式中属于最简二次根式的是( )
A. B. C. D.
解:A、=,即被开方数中含有分母,不是最简二次根式,故本选项不符合题意;
B、=,即被开方数中含有分母,不是最简二次根式,故本选项不符合题意;
C、=4,即被开方数中含有能开得尽方的因式,不是最简二次根式,故本选项不符合题意;
D、是最简二次根式,故本选项符合题意;
故选:D.
5.若点A(2,m)在正比例函数y=x的图象上,则m的值是( )
A. B.﹣ C.1 D.﹣1
解:∵点A(2,m)在正比例函数y=x的图象上,
∴m=×2=1.
故选:C.
6.下列计算正确的是( )
A.a2+a2=a4 B.2a2﹣a2=2 C.(a2)3=a5 D.a5?a2=a7
解:A.a2+a2=2a2,故本选项不符合题意;
B.2a2﹣a2=a2,故本选项不符合题意;
C.(a2)3=a6,故本选项不符合题意;
D.a5?a2=a7,故本选项符合题意;
故选:D.
7.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
解:原不等式组可化简为:.
∴在数轴上表示为:
故选:A.
8.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.一组对边平行且对角线相等的四边形是矩形
D.四条边都相等的四边形是菱形
解:A、∵两组对边分别相等的四边形是平行四边形,
∴选项A不符合题意;
B、∵四个内角都相等的四边形是矩形,
∴选项B不符合题意;
C、∵两组对边分别平行且对角线相等的四边形是矩形,
∴选项C符合题意;
D、∵四条边都相等的四边形是菱形,
∴选项D不符合题意;
故选:C.
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
解:设该店有客房x间,房客y人;
根据题意得:,
故选:A.
10.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x>4时,y1<y2;④b<0.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
解:根据图象y1=kx+b经过第一、二、四象限,
∴k<0,b>0,
故①正确,④错误;
∵y2=x+a与y轴负半轴相交,
∴a<0,
故②错误;
当x>4时,图象y2在y1的上方,所以y1<y2,故③正确.
所以正确的有①共2个.
故选:B.
二、填空题(每小题3分,共6题)
11.直线y=﹣x+1向上平移5个单位后,得到的直线的解析式是 y=﹣x+6 .
解:直线y=﹣x+1向上平移5个单位后,得到的直线的解析式是y=﹣x+1+5,即y=﹣x+6.
故答案为y=﹣x+6.
12.若在实数范围内有意义,则x的取值范围为 x≥2 .
解:由题意得:x﹣2≥0,
解得:x≥2,
故答案为:x≥2.
13.数据1,2,3,0,﹣3,﹣2,﹣1的中位数是 0 .
解:把数据按从小到大排列:﹣3,﹣2,﹣1,0,1,2,3,共有7个数,最中间一个数为0,所以这组数据的中位数为0.
故答案为:0.
14.在新年晚会的投飞镖游戏环节中,5名同学的投掷成绩(单位:环)分别是:7,8,7,10,8,则这组数据的方差是 1.2 .
解:根据题意,平均数==8,
方差s2=[(7﹣8)2+(8﹣8)2+(7﹣8)2+(10﹣8)2+(8﹣8)2]=1.2;
故答案为:1.2.
15.在直角三角形中,若两条直角边长分别为6cm和8cm,则斜边上的中线为 5 cm.
解:根据勾股定理得,斜边==10cm,
∴斜边上的中线=×斜边=×10=5cm.
故答案为:5.
16.如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC=.其中正确结论序号有: ①②③④⑤ .
解:①∵正方形ABCD,
∴AB=BC=CD=AD=12,∠B=∠GCE=∠D=90°,
由折叠的性质可得,AF=AD,∠AFE=∠D=90°,
∴∠AFG=90°=∠B,AB=AF,
∴Rt△ABG≌Rt△AFG(HL),
故①正确;
②∵∠BAG=∠FAG,∠DAE=∠FAE,
∴∠EAF=∠BAD=45°,
故②正确;
③由题意得EF=DE,GB=CG=GF=6,
设DE=EF=x,则CE=12﹣x,
在Rt△ECG中,(12﹣x)2+36=(x+6)2,
∴x=4,
∴DE=4,CE=8,
∴CE=2DE,
故③正确;
④∵CG=BG,BG=GF,
∴CG=GF,
∴∠GFC=∠GCF,
∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,
∵∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GCF,
∴∠AGB=∠GCF,
∴AG∥CF,
故④正确;
⑤∵S△GCE=×GC×CE=×6×8=24,
∵GF=6,EF=4,△GFC和△FCE等高,
∴S△GFC:S△FEC=3:2,
∴S△GFC=×24=,
故⑤正确;
故答案为①②③④⑤.
三、解答题(共9大题)
17.计算:(π﹣3.14)0+(﹣)﹣1﹣|1﹣|.
解:(π﹣3.14)0+(﹣)﹣1﹣|1﹣|
=1﹣2﹣(﹣1)
=﹣1+1﹣
=﹣.
18.先化简,再求值,÷,其中m=1.
解:÷
=?
=,
当m=1时,原式==﹣.
19.一次函数y=kx+b的图象如图所示:
(1)求出该一次函数的表达式;
(2)当x=10时,y的值是多少?
解:(1)观察函数图象,可知:点(2,0),(6,4)在函数y=kx+b的图象上,
∴,解得:,
∴该一次函数的表达式为y=x﹣2.
(2)当x=10时,y=10﹣2=8.
20.如图,四边形ABCD是平行四边形,E、F是对角线AC上的点,DE∥BF.
(1)求证:△AED≌△CFB;
(2)求证:AF=CE.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
∵DE∥BF,
∴∠DEF=∠BFE,
∴∠AED=∠CFB,
在△ADE和△CBF中,
,
∴△AED≌△CFB(AAS);
(2)∵△AED≌△CFB,
∴AE=CF,
∴AE+EF=CF+EF,
即:AF=CE.
21.某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) 频数(人数) 频率
0.5 12 0.12
1 30 0.3
1.5 x 0.5
2 8 y
合计 m 1
(1)统计表中的m= 100 ,x= 50 ,y= 0.08 ;
(2)被抽样调查的同学劳动时间的众数是 1.5 ,中位数是 1.5 ;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
解:(1)调查的总人数是m=12÷0.12=100(人),
则x=100×0.5=50(人),
y==0.08;
(2)被调查同学劳动时间的众数为1.5小时;中位数是1.5小时;
(3)
;
(4)所有被调查同学的平均劳动时间是:=1.27(小时).
22.如图,△ABC中,AB=AC,AD是BC边上的高,点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE是矩形;
(2)若OE=2,求AB的长.
【解答】(1)证明:∵点O是AC中点,
∴AO=CO,
又∵OE=OD,
∴四边形ADCE为平行四边形,
∵AD是BC边上的高,
∴AD⊥DC,
∴∠ADC=90°,
∴四边形ADCE为矩形;
(2)解:∵四边形ADCE为矩形,
∴OE=AO=2,
∵点O是AC中点,
∴AO=2,AC=4,
又∵AB=AC,
∴AB=4.
23.将220吨物资从A地运往甲、乙两地,用大、小两种货车共18辆,恰好一次性运完这批物资,已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
甲地(元/辆) 乙地(元/辆)
大货车 700 800
小货车 400 600
(1)这两种货车各需多少辆?
(2)如果安排8辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,请写出运费W(元)与a的函数关系式.若运往甲地的物资不少于110吨,请设计出货车调配方案,并求出最少运费.
解:(1)设需要大货车x辆,需要小货车y辆,根据题意得:
解得,
答:需要大货车8辆,需要小货车10辆;
(2)根据题意得:
W=700a+800(8﹣a)+400(8﹣a)+600(2+a),
W=100a+10800.
∵15a+10(8﹣a)≥110,
∴a≥6,
∵k=100>0,
∴W随a的增大而增大,
∴a=6时,W最小,最小值=11400,
∴运往甲地的大货车6辆,小货车2辆,运往乙地的大货车2辆,小货车8辆.最少运费为11400元.
24.对于平面直角坐标系xOy中的点P(x,y),若x,y满足|y﹣x|=1,则点P(x,y)就称为“完美点”.例如:(5,6),因为|6﹣5|=1,所以(5,6)是“完美点”.
(1)点M(3,2) 是 “完美点”;点N(﹣2,3) 不是 “完美点”(填“是”或“不是”);
(2)已知一次函数y=3x+m(m为常数)图象上有一个“完美点”的坐标是(1,2),一次函数y=3x+m(m为常数)图象上是否存在其他“完美点”?若存在,请求出来;若不存在,请说明理由.
(3)点A和点B为一次函数y=2x+a(a为常数且a<﹣2)图象上的两个“完美点”,点Q在x轴上运动,当QA+QB最小时,求点Q的坐标(用含字母a的式子表示).
解:(1)∵|3﹣2|=1,
∴点M(3,2)是“完美点”;
∵|﹣2﹣3|=5≠1,
∴点N(﹣2,3)不是“完美点”;
故答案为:是;不是;
(2)将点坐标(1,2)代入y=3x+m得,3+m=2;
∴m=﹣1,
∴y=3x﹣1,
又∵|x﹣y|=1,
∴y=x+1或y=x﹣1,
①当y=x+1时,
联立得:x+1=3x﹣1,
解得x=1代入得y=2,
所以(1,2)为其本身,
②当y=x﹣1时,
联立得:x﹣1=2x﹣1,
解得x=0代入得y=﹣1,
所以为另一个点坐标(0,﹣1),
综上所述,存在其他“完美点”为(0,﹣1);
(3)由题意得“完美点”在函数y=x+1或y=x﹣1图象上,
①当在函数y=x+1上时,2x+a=x+1,
解得x=1﹣a,
代入得y=1﹣a+1=2﹣a,
∴A为(1﹣a,2﹣a),
②当在函数y=x﹣1上时,2x+a=x﹣1,
解得x=﹣1﹣a,
代入得y=﹣1﹣a﹣1=﹣2﹣a,
∴B为(﹣1﹣a,﹣2﹣a),
∵a<﹣2,
∴A、B都在第一象限.
点A关于x轴的对称点为A'(1﹣a,a﹣2),
设直线A′B的解析式为yA′B=kx+b,
代入点A′、B得,
解得:,
∴直线A′B的解析式为yA′B=ax+a2﹣2,
令yA′B=0,
解得:x=,
∴点Q为(,0).
25.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.
解:(1)∵点A的坐标为(3,0)
∴AO=3
∵∠ABO=30°,∠AOB=90°
∴BO=AO=3,AB=2OA=6,∠OAB=60°,
又∵AB⊥BC
∴∠ACB=30°
∴AC=2AB=12
∴OC=AC﹣OA=12﹣3=9
∵OC=9,OB=3
∴点B(0,3),点C(﹣9,0)
设直线BC解析式y=kx+b
解得:k=,b=3
∴直线BC解析式y=x+3
设直线AB解析式y=mx+n
解得:m=﹣,n=3
∴直线AB解析式y=﹣x+3
(2)
∵折叠,点O与点B重合
∴DE是BO的垂直平分线
∴EO=BE,BD=OD
∴∠EBO=∠EOB,∠DBO=∠DOB
∵BO⊥CO
∴∠EBO+∠ECO=90°,∠EOB+∠EOC=90°
∴∠EOC=∠ECO
∴CE=EO
∴CE=BE
同理BD=DA
∴DE=AC=6
∵点A(3,0),点B(0,3),点C(﹣9,0)
∴点E(﹣,),点D(,)
设点F(x,0)
∵△EFD是直角三角形,DE是斜边
∴DE2=EF2+DF2.
∴36=(x+)2++(x﹣)2+
解得:x1=0,x2=﹣3
∴点F(0,0)或(﹣3,0)
(3)若BC为边,在BC上方和下方作正方形,如图:四边形BCFE是正方形,四边形BCMN是正方形
过点F作FH⊥AC于点H,过点E作EG⊥BO于点G
∵四边形BCFE是正方形
∴BC=CF,∠BCF=90°
∴∠BCO+∠FCH=90°,且∠FCH+∠CFH=90°
∴∠BCO=∠CFH且∠BOC=∠CHF=90°,BC=CF
∴△BCO≌△CFO(AAS)
∴CH=OB=3,HF=CO=9
∴OH=9﹣3
∴点F(﹣9+3,﹣9)
同理可得△BEG≌△CBO
∴BG=CO=9,GE=BO=3
∴OG=9﹣3
∴点E(3,﹣9+3)
同理可得:点M(﹣9﹣3,9),点N(﹣3,9+3)
若BC为对角线,如图:四边形BECF是正方形
过点F作FM⊥CO于点M,作FN⊥BO于点 N
∵FM⊥CO,FN⊥BO,BO⊥CO
∴四边形OMFN是矩形
∴OM=FN,ON=FM
∵四边形BECF是正方形
∴CF=BF,∠CFB=90°
∵∠CFB=∠COB=90°
∴点C,点B,点O,点F四点共圆
∴∠FCO=∠OBF,且CF=BF,∠FMC=∠FNB=90°
∴△FMC≌△FNB(AAS)
∴FM=FN,CM=BN
∴边形FNOM是正方形
∴OM=ON=FM=FN
∵CM+OM=9,BN﹣ON=3
∴OM=ON=,CM=BN=
∴点F(,)
同理可求点E坐标为(,),
综上所述:这两点的坐标为(﹣9﹣3,9),(﹣3,9+3)或(,)或(,).
一、选择题(每题3分).
1.下列“表情图”中,属于轴对称图形的是( )
A. B.
C. D.
2.我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )
A.0.3×106 B.3×107 C.3×106 D.30×105
3.下列四组线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
4.下列各式中属于最简二次根式的是( )
A. B. C. D.
5.若点A(2,m)在正比例函数y=x的图象上,则m的值是( )
A. B.﹣ C.1 D.﹣1
6.下列计算正确的是( )
A.a2+a2=a4 B.2a2﹣a2=2 C.(a2)3=a5 D.a5?a2=a7
7.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
8.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.一组对边平行且对角线相等的四边形是矩形
D.四条边都相等的四边形是菱形
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
10.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x>4时,y1<y2;④b<0.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共6题)
11.直线y=﹣x+1向上平移5个单位后,得到的直线的解析式是 .
12.若在实数范围内有意义,则x的取值范围为 .
13.数据1,2,3,0,﹣3,﹣2,﹣1的中位数是 .
14.在新年晚会的投飞镖游戏环节中,5名同学的投掷成绩(单位:环)分别是:7,8,7,10,8,则这组数据的方差是 .
15.在直角三角形中,若两条直角边长分别为6cm和8cm,则斜边上的中线为 cm.
16.如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC=.其中正确结论序号有: .
三、解答题(共9大题)
17.计算:(π﹣3.14)0+(﹣)﹣1﹣|1﹣|.
18.先化简,再求值,÷,其中m=1.
19.一次函数y=kx+b的图象如图所示:
(1)求出该一次函数的表达式;
(2)当x=10时,y的值是多少?
20.如图,四边形ABCD是平行四边形,E、F是对角线AC上的点,DE∥BF.
(1)求证:△AED≌△CFB;
(2)求证:AF=CE.
21.某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) 频数(人数) 频率
0.5 12 0.12
1 30 0.3
1.5 x 0.5
2 8 y
合计 m 1
(1)统计表中的m= ,x= ,y= ;
(2)被抽样调查的同学劳动时间的众数是 ,中位数是 ;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
22.如图,△ABC中,AB=AC,AD是BC边上的高,点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE是矩形;
(2)若OE=2,求AB的长.
23.将220吨物资从A地运往甲、乙两地,用大、小两种货车共18辆,恰好一次性运完这批物资,已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
甲地(元/辆) 乙地(元/辆)
大货车 700 800
小货车 400 600
(1)这两种货车各需多少辆?
(2)如果安排8辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,请写出运费W(元)与a的函数关系式.若运往甲地的物资不少于110吨,请设计出货车调配方案,并求出最少运费.
24.对于平面直角坐标系xOy中的点P(x,y),若x,y满足|y﹣x|=1,则点P(x,y)就称为“完美点”.例如:(5,6),因为|6﹣5|=1,所以(5,6)是“完美点”.
(1)点M(3,2) “完美点”;点N(﹣2,3) “完美点”(填“是”或“不是”);
(2)已知一次函数y=3x+m(m为常数)图象上有一个“完美点”的坐标是(1,2),一次函数y=3x+m(m为常数)图象上是否存在其他“完美点”?若存在,请求出来;若不存在,请说明理由.
(3)点A和点B为一次函数y=2x+a(a为常数且a<﹣2)图象上的两个“完美点”,点Q在x轴上运动,当QA+QB最小时,求点Q的坐标(用含字母a的式子表示).
25.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共10题)
1.下列“表情图”中,属于轴对称图形的是( )
A. B.
C. D.
解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确;
故选:D.
2.我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )
A.0.3×106 B.3×107 C.3×106 D.30×105
解:3000000=3×106,
故选:C.
3.下列四组线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
解:A、12+22≠32,不能构成直角三角形,故不符合题意;
B、22+32≠42,不能构成直角三角形,故不符合题意;
C、32+42=52,能构成直角三角形,故符合题意;
D、42+52≠62,不能构成直角三角形,故不符合题意.
故选:C.
4.下列各式中属于最简二次根式的是( )
A. B. C. D.
解:A、=,即被开方数中含有分母,不是最简二次根式,故本选项不符合题意;
B、=,即被开方数中含有分母,不是最简二次根式,故本选项不符合题意;
C、=4,即被开方数中含有能开得尽方的因式,不是最简二次根式,故本选项不符合题意;
D、是最简二次根式,故本选项符合题意;
故选:D.
5.若点A(2,m)在正比例函数y=x的图象上,则m的值是( )
A. B.﹣ C.1 D.﹣1
解:∵点A(2,m)在正比例函数y=x的图象上,
∴m=×2=1.
故选:C.
6.下列计算正确的是( )
A.a2+a2=a4 B.2a2﹣a2=2 C.(a2)3=a5 D.a5?a2=a7
解:A.a2+a2=2a2,故本选项不符合题意;
B.2a2﹣a2=a2,故本选项不符合题意;
C.(a2)3=a6,故本选项不符合题意;
D.a5?a2=a7,故本选项符合题意;
故选:D.
7.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
解:原不等式组可化简为:.
∴在数轴上表示为:
故选:A.
8.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.一组对边平行且对角线相等的四边形是矩形
D.四条边都相等的四边形是菱形
解:A、∵两组对边分别相等的四边形是平行四边形,
∴选项A不符合题意;
B、∵四个内角都相等的四边形是矩形,
∴选项B不符合题意;
C、∵两组对边分别平行且对角线相等的四边形是矩形,
∴选项C符合题意;
D、∵四条边都相等的四边形是菱形,
∴选项D不符合题意;
故选:C.
9.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )
A. B.
C. D.
解:设该店有客房x间,房客y人;
根据题意得:,
故选:A.
10.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x>4时,y1<y2;④b<0.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
解:根据图象y1=kx+b经过第一、二、四象限,
∴k<0,b>0,
故①正确,④错误;
∵y2=x+a与y轴负半轴相交,
∴a<0,
故②错误;
当x>4时,图象y2在y1的上方,所以y1<y2,故③正确.
所以正确的有①共2个.
故选:B.
二、填空题(每小题3分,共6题)
11.直线y=﹣x+1向上平移5个单位后,得到的直线的解析式是 y=﹣x+6 .
解:直线y=﹣x+1向上平移5个单位后,得到的直线的解析式是y=﹣x+1+5,即y=﹣x+6.
故答案为y=﹣x+6.
12.若在实数范围内有意义,则x的取值范围为 x≥2 .
解:由题意得:x﹣2≥0,
解得:x≥2,
故答案为:x≥2.
13.数据1,2,3,0,﹣3,﹣2,﹣1的中位数是 0 .
解:把数据按从小到大排列:﹣3,﹣2,﹣1,0,1,2,3,共有7个数,最中间一个数为0,所以这组数据的中位数为0.
故答案为:0.
14.在新年晚会的投飞镖游戏环节中,5名同学的投掷成绩(单位:环)分别是:7,8,7,10,8,则这组数据的方差是 1.2 .
解:根据题意,平均数==8,
方差s2=[(7﹣8)2+(8﹣8)2+(7﹣8)2+(10﹣8)2+(8﹣8)2]=1.2;
故答案为:1.2.
15.在直角三角形中,若两条直角边长分别为6cm和8cm,则斜边上的中线为 5 cm.
解:根据勾股定理得,斜边==10cm,
∴斜边上的中线=×斜边=×10=5cm.
故答案为:5.
16.如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC=.其中正确结论序号有: ①②③④⑤ .
解:①∵正方形ABCD,
∴AB=BC=CD=AD=12,∠B=∠GCE=∠D=90°,
由折叠的性质可得,AF=AD,∠AFE=∠D=90°,
∴∠AFG=90°=∠B,AB=AF,
∴Rt△ABG≌Rt△AFG(HL),
故①正确;
②∵∠BAG=∠FAG,∠DAE=∠FAE,
∴∠EAF=∠BAD=45°,
故②正确;
③由题意得EF=DE,GB=CG=GF=6,
设DE=EF=x,则CE=12﹣x,
在Rt△ECG中,(12﹣x)2+36=(x+6)2,
∴x=4,
∴DE=4,CE=8,
∴CE=2DE,
故③正确;
④∵CG=BG,BG=GF,
∴CG=GF,
∴∠GFC=∠GCF,
∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,
∵∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GCF,
∴∠AGB=∠GCF,
∴AG∥CF,
故④正确;
⑤∵S△GCE=×GC×CE=×6×8=24,
∵GF=6,EF=4,△GFC和△FCE等高,
∴S△GFC:S△FEC=3:2,
∴S△GFC=×24=,
故⑤正确;
故答案为①②③④⑤.
三、解答题(共9大题)
17.计算:(π﹣3.14)0+(﹣)﹣1﹣|1﹣|.
解:(π﹣3.14)0+(﹣)﹣1﹣|1﹣|
=1﹣2﹣(﹣1)
=﹣1+1﹣
=﹣.
18.先化简,再求值,÷,其中m=1.
解:÷
=?
=,
当m=1时,原式==﹣.
19.一次函数y=kx+b的图象如图所示:
(1)求出该一次函数的表达式;
(2)当x=10时,y的值是多少?
解:(1)观察函数图象,可知:点(2,0),(6,4)在函数y=kx+b的图象上,
∴,解得:,
∴该一次函数的表达式为y=x﹣2.
(2)当x=10时,y=10﹣2=8.
20.如图,四边形ABCD是平行四边形,E、F是对角线AC上的点,DE∥BF.
(1)求证:△AED≌△CFB;
(2)求证:AF=CE.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
∵DE∥BF,
∴∠DEF=∠BFE,
∴∠AED=∠CFB,
在△ADE和△CBF中,
,
∴△AED≌△CFB(AAS);
(2)∵△AED≌△CFB,
∴AE=CF,
∴AE+EF=CF+EF,
即:AF=CE.
21.某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) 频数(人数) 频率
0.5 12 0.12
1 30 0.3
1.5 x 0.5
2 8 y
合计 m 1
(1)统计表中的m= 100 ,x= 50 ,y= 0.08 ;
(2)被抽样调查的同学劳动时间的众数是 1.5 ,中位数是 1.5 ;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
解:(1)调查的总人数是m=12÷0.12=100(人),
则x=100×0.5=50(人),
y==0.08;
(2)被调查同学劳动时间的众数为1.5小时;中位数是1.5小时;
(3)
;
(4)所有被调查同学的平均劳动时间是:=1.27(小时).
22.如图,△ABC中,AB=AC,AD是BC边上的高,点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE是矩形;
(2)若OE=2,求AB的长.
【解答】(1)证明:∵点O是AC中点,
∴AO=CO,
又∵OE=OD,
∴四边形ADCE为平行四边形,
∵AD是BC边上的高,
∴AD⊥DC,
∴∠ADC=90°,
∴四边形ADCE为矩形;
(2)解:∵四边形ADCE为矩形,
∴OE=AO=2,
∵点O是AC中点,
∴AO=2,AC=4,
又∵AB=AC,
∴AB=4.
23.将220吨物资从A地运往甲、乙两地,用大、小两种货车共18辆,恰好一次性运完这批物资,已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
甲地(元/辆) 乙地(元/辆)
大货车 700 800
小货车 400 600
(1)这两种货车各需多少辆?
(2)如果安排8辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,请写出运费W(元)与a的函数关系式.若运往甲地的物资不少于110吨,请设计出货车调配方案,并求出最少运费.
解:(1)设需要大货车x辆,需要小货车y辆,根据题意得:
解得,
答:需要大货车8辆,需要小货车10辆;
(2)根据题意得:
W=700a+800(8﹣a)+400(8﹣a)+600(2+a),
W=100a+10800.
∵15a+10(8﹣a)≥110,
∴a≥6,
∵k=100>0,
∴W随a的增大而增大,
∴a=6时,W最小,最小值=11400,
∴运往甲地的大货车6辆,小货车2辆,运往乙地的大货车2辆,小货车8辆.最少运费为11400元.
24.对于平面直角坐标系xOy中的点P(x,y),若x,y满足|y﹣x|=1,则点P(x,y)就称为“完美点”.例如:(5,6),因为|6﹣5|=1,所以(5,6)是“完美点”.
(1)点M(3,2) 是 “完美点”;点N(﹣2,3) 不是 “完美点”(填“是”或“不是”);
(2)已知一次函数y=3x+m(m为常数)图象上有一个“完美点”的坐标是(1,2),一次函数y=3x+m(m为常数)图象上是否存在其他“完美点”?若存在,请求出来;若不存在,请说明理由.
(3)点A和点B为一次函数y=2x+a(a为常数且a<﹣2)图象上的两个“完美点”,点Q在x轴上运动,当QA+QB最小时,求点Q的坐标(用含字母a的式子表示).
解:(1)∵|3﹣2|=1,
∴点M(3,2)是“完美点”;
∵|﹣2﹣3|=5≠1,
∴点N(﹣2,3)不是“完美点”;
故答案为:是;不是;
(2)将点坐标(1,2)代入y=3x+m得,3+m=2;
∴m=﹣1,
∴y=3x﹣1,
又∵|x﹣y|=1,
∴y=x+1或y=x﹣1,
①当y=x+1时,
联立得:x+1=3x﹣1,
解得x=1代入得y=2,
所以(1,2)为其本身,
②当y=x﹣1时,
联立得:x﹣1=2x﹣1,
解得x=0代入得y=﹣1,
所以为另一个点坐标(0,﹣1),
综上所述,存在其他“完美点”为(0,﹣1);
(3)由题意得“完美点”在函数y=x+1或y=x﹣1图象上,
①当在函数y=x+1上时,2x+a=x+1,
解得x=1﹣a,
代入得y=1﹣a+1=2﹣a,
∴A为(1﹣a,2﹣a),
②当在函数y=x﹣1上时,2x+a=x﹣1,
解得x=﹣1﹣a,
代入得y=﹣1﹣a﹣1=﹣2﹣a,
∴B为(﹣1﹣a,﹣2﹣a),
∵a<﹣2,
∴A、B都在第一象限.
点A关于x轴的对称点为A'(1﹣a,a﹣2),
设直线A′B的解析式为yA′B=kx+b,
代入点A′、B得,
解得:,
∴直线A′B的解析式为yA′B=ax+a2﹣2,
令yA′B=0,
解得:x=,
∴点Q为(,0).
25.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.
解:(1)∵点A的坐标为(3,0)
∴AO=3
∵∠ABO=30°,∠AOB=90°
∴BO=AO=3,AB=2OA=6,∠OAB=60°,
又∵AB⊥BC
∴∠ACB=30°
∴AC=2AB=12
∴OC=AC﹣OA=12﹣3=9
∵OC=9,OB=3
∴点B(0,3),点C(﹣9,0)
设直线BC解析式y=kx+b
解得:k=,b=3
∴直线BC解析式y=x+3
设直线AB解析式y=mx+n
解得:m=﹣,n=3
∴直线AB解析式y=﹣x+3
(2)
∵折叠,点O与点B重合
∴DE是BO的垂直平分线
∴EO=BE,BD=OD
∴∠EBO=∠EOB,∠DBO=∠DOB
∵BO⊥CO
∴∠EBO+∠ECO=90°,∠EOB+∠EOC=90°
∴∠EOC=∠ECO
∴CE=EO
∴CE=BE
同理BD=DA
∴DE=AC=6
∵点A(3,0),点B(0,3),点C(﹣9,0)
∴点E(﹣,),点D(,)
设点F(x,0)
∵△EFD是直角三角形,DE是斜边
∴DE2=EF2+DF2.
∴36=(x+)2++(x﹣)2+
解得:x1=0,x2=﹣3
∴点F(0,0)或(﹣3,0)
(3)若BC为边,在BC上方和下方作正方形,如图:四边形BCFE是正方形,四边形BCMN是正方形
过点F作FH⊥AC于点H,过点E作EG⊥BO于点G
∵四边形BCFE是正方形
∴BC=CF,∠BCF=90°
∴∠BCO+∠FCH=90°,且∠FCH+∠CFH=90°
∴∠BCO=∠CFH且∠BOC=∠CHF=90°,BC=CF
∴△BCO≌△CFO(AAS)
∴CH=OB=3,HF=CO=9
∴OH=9﹣3
∴点F(﹣9+3,﹣9)
同理可得△BEG≌△CBO
∴BG=CO=9,GE=BO=3
∴OG=9﹣3
∴点E(3,﹣9+3)
同理可得:点M(﹣9﹣3,9),点N(﹣3,9+3)
若BC为对角线,如图:四边形BECF是正方形
过点F作FM⊥CO于点M,作FN⊥BO于点 N
∵FM⊥CO,FN⊥BO,BO⊥CO
∴四边形OMFN是矩形
∴OM=FN,ON=FM
∵四边形BECF是正方形
∴CF=BF,∠CFB=90°
∵∠CFB=∠COB=90°
∴点C,点B,点O,点F四点共圆
∴∠FCO=∠OBF,且CF=BF,∠FMC=∠FNB=90°
∴△FMC≌△FNB(AAS)
∴FM=FN,CM=BN
∴边形FNOM是正方形
∴OM=ON=FM=FN
∵CM+OM=9,BN﹣ON=3
∴OM=ON=,CM=BN=
∴点F(,)
同理可求点E坐标为(,),
综上所述:这两点的坐标为(﹣9﹣3,9),(﹣3,9+3)或(,)或(,).
同课章节目录
