1.3勾股定理的应用学案 2021年暑假自主学习八年级数学北师大版上册(无答案)
文档属性
| 名称 | 1.3勾股定理的应用学案 2021年暑假自主学习八年级数学北师大版上册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 283.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 00:00:00 | ||
图片预览

文档简介
1.3勾股定理的应用
知识点一?圆柱侧面上两点间的最短距离
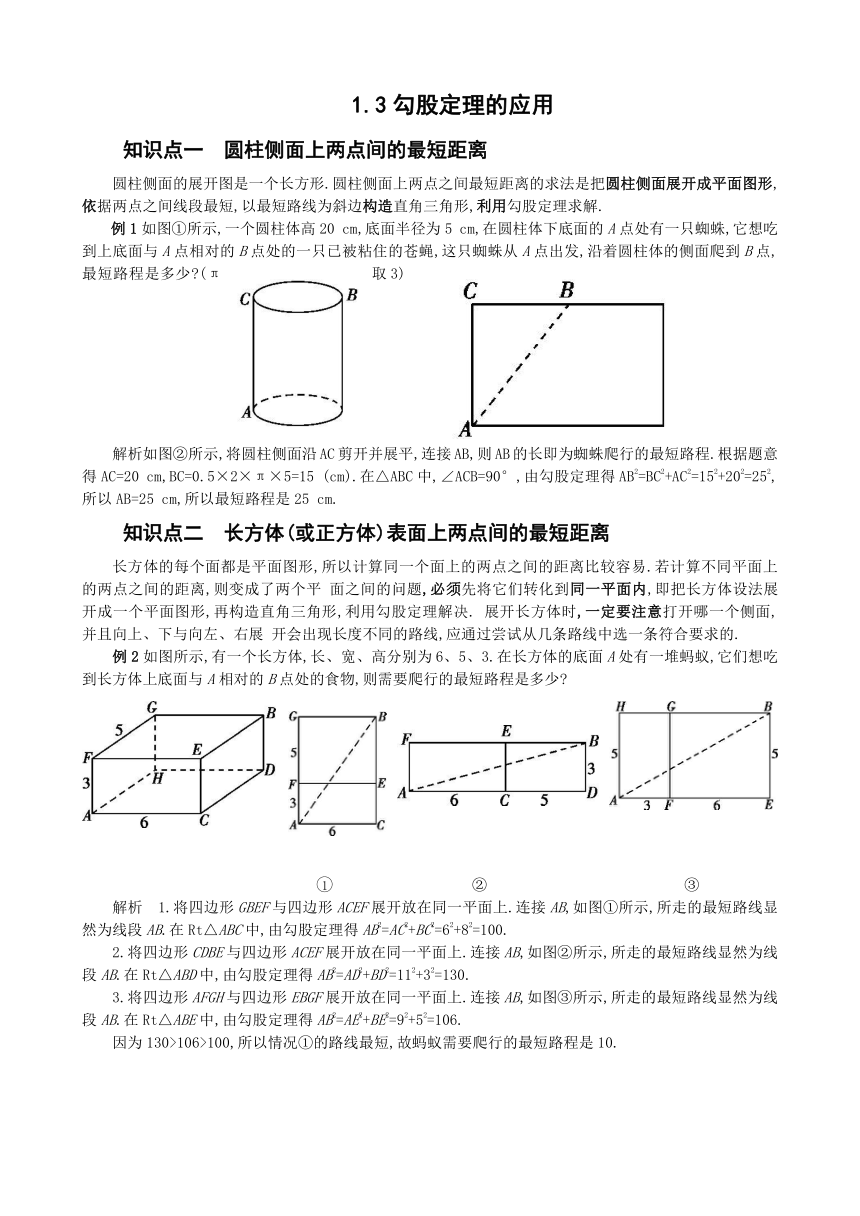
圆柱侧面的展开图是一个长方形.圆柱侧面上两点之间最短距离的求法是把圆柱侧面展开成平面图形,依据两点之间线段最短,以最短路线为斜边构造直角三角形,利用勾股定理求解.
例1如图①所示,一个圆柱体高20
cm,底面半径为5
cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)
②
解析如图②所示,将圆柱侧面沿AC剪开并展平,连接AB,则AB的长即为蜘蛛爬行的最短路程.根据题意得AC=20
cm,BC=0.5×2×π×5=15
(cm).在△ABC中,∠ACB=90°,由勾股定理得AB2=BC2+AC2=152+202=252,所以AB=25
cm,所以最短路程是25
cm.
知识点二?长方体(或正方体)表面上两点间的最短距离
长方体的每个面都是平面图形,所以计算同一个面上的两点之间的距离比较容易.若计算不同平面上的两点之间的距离,则变成了两个平
面之间的问题,必须先将它们转化到同一平面内,即把长方体设法展开成一个平面图形,再构造直角三角形,利用勾股定理解决.
展开长方体时,一定要注意打开哪一个侧面,并且向上、下与向左、右展
开会出现长度不同的路线,应通过尝试从几条路线中选一条符合要求的.
例2如图所示,有一个长方体,长、宽、高分别为6、5、3.在长方体的底面A处有一堆蚂蚁,它们想吃到长方体上底面与A相对的B点处的食物,则需要爬行的最短路程是多少?
②
③
解析 1.将四边形GBEF与四边形ACEF展开放在同一平面上.连接AB,如图①所示,所走的最短路线显然为线段AB.在Rt△ABC中,由勾股定理得AB2=AC2+BC2=62+82=100.
2.将四边形CDBE与四边形ACEF展开放在同一平面上.连接AB,如图②所示,所走的最短路线显然为线段AB.在Rt△ABD中,由勾股定理得AB2=AD2+BD2=112+32=130.
3.将四边形AFGH与四边形EBGF展开放在同一平面上.连接AB,如图③所示,所走的最短路线显然为线段AB.在Rt△ABE中,由勾股定理得AB2=AE2+BE2=92+52=106.
因为130>106>100,所以情况①的路线最短,故蚂蚁需要爬行的最短路程是10.
巩固练习:基础篇
1.如图,若圆柱的底面周长是30
cm,高是40
cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是(
)A.80
cm
B.70
cm
C.60
cm
D.50
cm
(第1题图)
(第2题图)
(第3题图)
(第4题图)
2.如图所示,正方体的边长为1,一只蜘蛛从正方体的一个顶点A爬行到另一个顶点B,则蜘蛛爬行的最短距离的平方是(
)A.2
B.3
C.4
D.5
3.如图是一个三级台阶,它的每一级的长、宽、高分别为20
dm,3
dm,2
dm,A和B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬行到B点的最短路程为
。
4.如图,一棵大树在一次强台风中距地面5
m处折断,倒下后树顶端着地点A距树底端B的距离为12
m,这棵大树在折断前的高度为(
)A.10
m
B.15
m
C.18
m
D.20
m
5.如图,在长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5,BF=3,则CD的长是(
)A.7
B.8
C.9
D.10
(第5题图)
(第6题图)
(第7题图)
(第8题图)
6.如图,某会展中心在会展期间准备将高5
m,长13
m,宽2
m的楼梯铺上地毯,已知地毯每平方米30元,请你帮助计算一下,铺完这个楼梯至少需要_____________元钱.
7.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直,如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为(
)
A.600
m
B.500
m
C.400
m
D.300
m
8.如图,小明在广场上先向东走10
m,又向南走40
m,再向西走20
m,又向南走40
m,再向东走70
m.求小明到达的终止点与原出发点的距离.
巩固练习:提高篇
9.如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=π,S2=2π,则S3是(
)A.π
B.π
C.π
D.π
(第9题图)
(第10题图)
(第12题图)
(第13题图)
10.如图,将一根长为24
cm的筷子,置于底面直径为5
cm,高为12
cm的圆柱形水杯中,设筷子露出杯子外面的长为
h
cm,则h的取值范围是__________________________.
11.在Rt△ABC中,∠C=90°,BC=6
cm,CA=8
cm,动点P从C点出发,以每秒2cm的速度沿CA,AB运动到点B,则点P从点C出发____________秒时,可使S△BCP=S△ABC.
12.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是________尺.
13.如图,圆柱形容器高为18
cm,底面周长为24
cm,在杯内壁离杯底4
cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2
cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为
.
14.如图,一张直角三角形纸片,两直角边AC=6
cm,BC=8
cm,∠C=90°,现将三角形沿AD对折,直角边AC落在AB上,点C落在点E处,求折叠后重合部分△ADE的面积.
15.如图,某居民楼A与公路MN相距60
m(AB=60
m),在公路MN上行驶的汽车在距居民楼A100
m的点P处就可使其受到噪音的影响,求在公路上以10
m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.
知识点一?圆柱侧面上两点间的最短距离
圆柱侧面的展开图是一个长方形.圆柱侧面上两点之间最短距离的求法是把圆柱侧面展开成平面图形,依据两点之间线段最短,以最短路线为斜边构造直角三角形,利用勾股定理求解.
例1如图①所示,一个圆柱体高20
cm,底面半径为5
cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)
②
解析如图②所示,将圆柱侧面沿AC剪开并展平,连接AB,则AB的长即为蜘蛛爬行的最短路程.根据题意得AC=20
cm,BC=0.5×2×π×5=15
(cm).在△ABC中,∠ACB=90°,由勾股定理得AB2=BC2+AC2=152+202=252,所以AB=25
cm,所以最短路程是25
cm.
知识点二?长方体(或正方体)表面上两点间的最短距离
长方体的每个面都是平面图形,所以计算同一个面上的两点之间的距离比较容易.若计算不同平面上的两点之间的距离,则变成了两个平
面之间的问题,必须先将它们转化到同一平面内,即把长方体设法展开成一个平面图形,再构造直角三角形,利用勾股定理解决.
展开长方体时,一定要注意打开哪一个侧面,并且向上、下与向左、右展
开会出现长度不同的路线,应通过尝试从几条路线中选一条符合要求的.
例2如图所示,有一个长方体,长、宽、高分别为6、5、3.在长方体的底面A处有一堆蚂蚁,它们想吃到长方体上底面与A相对的B点处的食物,则需要爬行的最短路程是多少?
②
③
解析 1.将四边形GBEF与四边形ACEF展开放在同一平面上.连接AB,如图①所示,所走的最短路线显然为线段AB.在Rt△ABC中,由勾股定理得AB2=AC2+BC2=62+82=100.
2.将四边形CDBE与四边形ACEF展开放在同一平面上.连接AB,如图②所示,所走的最短路线显然为线段AB.在Rt△ABD中,由勾股定理得AB2=AD2+BD2=112+32=130.
3.将四边形AFGH与四边形EBGF展开放在同一平面上.连接AB,如图③所示,所走的最短路线显然为线段AB.在Rt△ABE中,由勾股定理得AB2=AE2+BE2=92+52=106.
因为130>106>100,所以情况①的路线最短,故蚂蚁需要爬行的最短路程是10.
巩固练习:基础篇
1.如图,若圆柱的底面周长是30
cm,高是40
cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是(
)A.80
cm
B.70
cm
C.60
cm
D.50
cm
(第1题图)
(第2题图)
(第3题图)
(第4题图)
2.如图所示,正方体的边长为1,一只蜘蛛从正方体的一个顶点A爬行到另一个顶点B,则蜘蛛爬行的最短距离的平方是(
)A.2
B.3
C.4
D.5
3.如图是一个三级台阶,它的每一级的长、宽、高分别为20
dm,3
dm,2
dm,A和B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬行到B点的最短路程为
。
4.如图,一棵大树在一次强台风中距地面5
m处折断,倒下后树顶端着地点A距树底端B的距离为12
m,这棵大树在折断前的高度为(
)A.10
m
B.15
m
C.18
m
D.20
m
5.如图,在长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AE=5,BF=3,则CD的长是(
)A.7
B.8
C.9
D.10
(第5题图)
(第6题图)
(第7题图)
(第8题图)
6.如图,某会展中心在会展期间准备将高5
m,长13
m,宽2
m的楼梯铺上地毯,已知地毯每平方米30元,请你帮助计算一下,铺完这个楼梯至少需要_____________元钱.
7.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直,如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为(
)
A.600
m
B.500
m
C.400
m
D.300
m
8.如图,小明在广场上先向东走10
m,又向南走40
m,再向西走20
m,又向南走40
m,再向东走70
m.求小明到达的终止点与原出发点的距离.
巩固练习:提高篇
9.如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=π,S2=2π,则S3是(
)A.π
B.π
C.π
D.π
(第9题图)
(第10题图)
(第12题图)
(第13题图)
10.如图,将一根长为24
cm的筷子,置于底面直径为5
cm,高为12
cm的圆柱形水杯中,设筷子露出杯子外面的长为
h
cm,则h的取值范围是__________________________.
11.在Rt△ABC中,∠C=90°,BC=6
cm,CA=8
cm,动点P从C点出发,以每秒2cm的速度沿CA,AB运动到点B,则点P从点C出发____________秒时,可使S△BCP=S△ABC.
12.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是________尺.
13.如图,圆柱形容器高为18
cm,底面周长为24
cm,在杯内壁离杯底4
cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2
cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为
.
14.如图,一张直角三角形纸片,两直角边AC=6
cm,BC=8
cm,∠C=90°,现将三角形沿AD对折,直角边AC落在AB上,点C落在点E处,求折叠后重合部分△ADE的面积.
15.如图,某居民楼A与公路MN相距60
m(AB=60
m),在公路MN上行驶的汽车在距居民楼A100
m的点P处就可使其受到噪音的影响,求在公路上以10
m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.
同课章节目录
