2021-2022学年北师大版数学 八年级上册1.3 勾股定理的应用 课件(共47张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学 八年级上册1.3 勾股定理的应用 课件(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 16:49:06 | ||
图片预览




文档简介
北师大版 数学 八年级上册
第一章 勾股定理
1.3 勾股定理的应用
1.灵活会用勾股定理求解立体图形上两点之间的最短距离问题。
2.运用勾股定理及其逆定理解决简单的实际问题。
学习目标
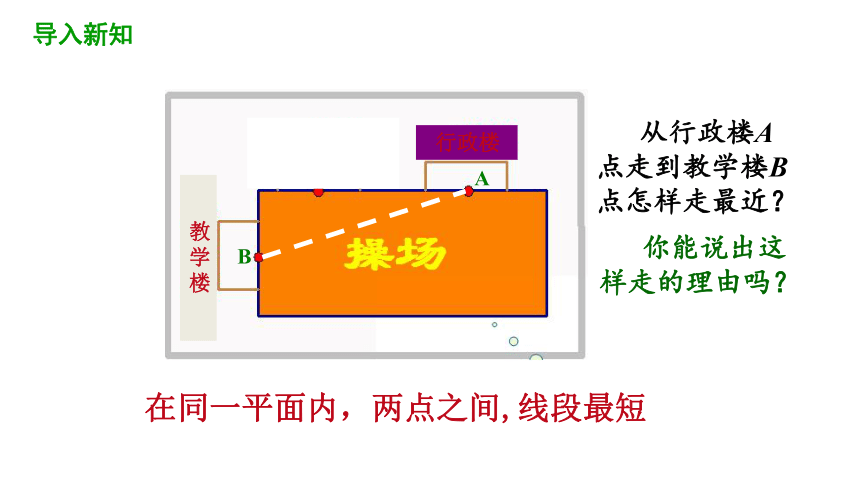
在同一平面内,两点之间,线段最短
从行政楼A点走到教学楼B点怎样走最近?
教学楼
行政楼
B
A
你能说出这样走的理由吗?
导入新知
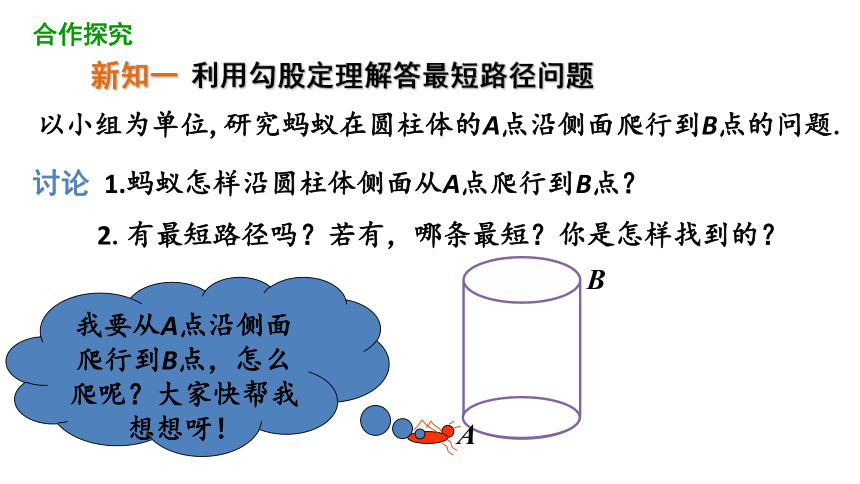
以小组为单位,研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题.
讨论 1.蚂蚁怎样沿圆柱体侧面从A点爬行到B点?
2.有最短路径吗?若有,哪条最短?你是怎样找到的?
B
A
我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!
新知一 利用勾股定理解答最短路径问题
合作探究
B
A
d
A
B
A'
A
B
B
A
O
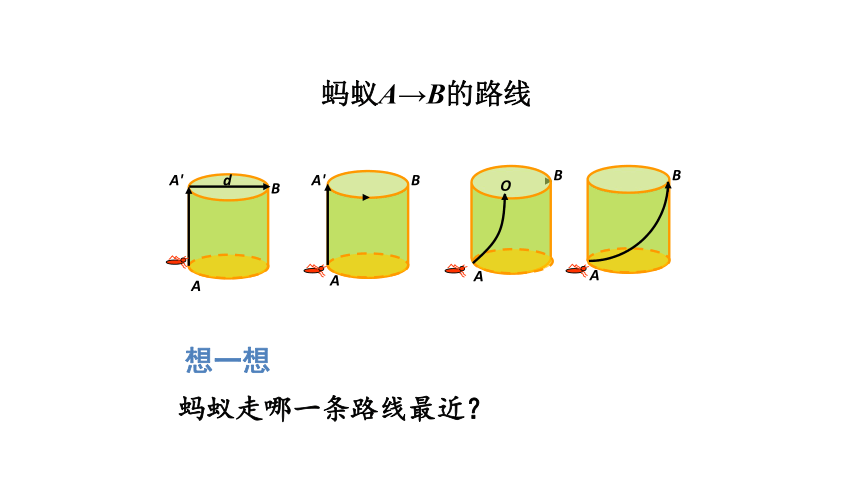
想一想
蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
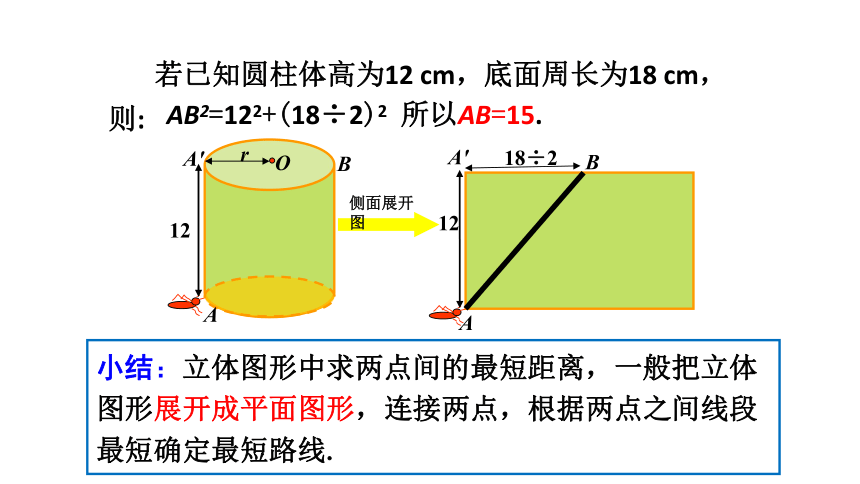
若已知圆柱体高为12 cm,底面周长为18 cm,则:
B
A
r
O
12
侧面展开图
12
18÷2
A
B
小结:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
A'
A'
AB2=122+(18÷2)2 所以AB=15.
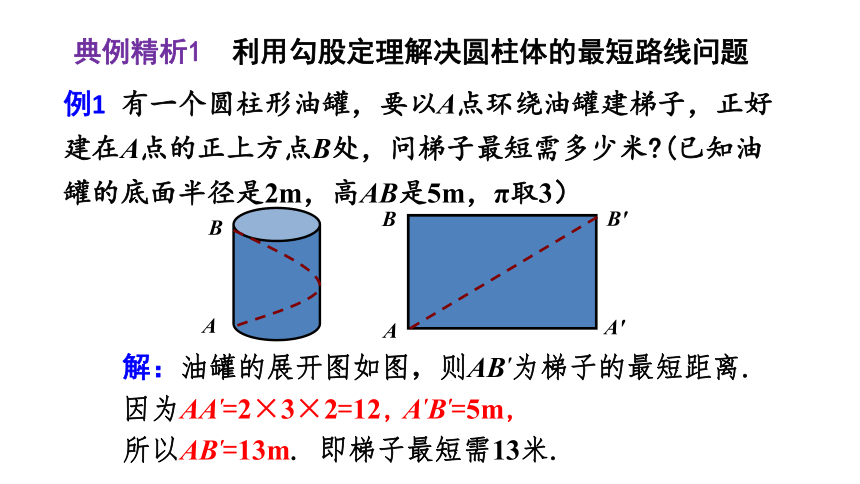
例1 有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米?(已知油罐的底面半径是2m,高AB是5m,π取3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则AB'为梯子的最短距离.
因为AA'=2×3×2=12, A'B'=5m,
所以AB'=13m. 即梯子最短需13米.
典例精析1 利用勾股定理解决圆柱体的最短路线问题
数学思想:
立体图形
平面图形
转化
展开
如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)
3 勾股定理的应用
巩固新知
解:如图所示,将圆柱侧面沿AC剪开并展平,连接AB,则AB的长即为蜘蛛爬行的最短路程.
根据题意得AC=20 cm,BC=????????×2×π×5=15(cm).
在△ABC中,∠ACB=90°,由勾股定理得
AB2=BC2+AC2=152+202=252,
所以AB=25 cm,最短路程是25cm.
?
3 勾股定理的应用
B
牛奶盒
A
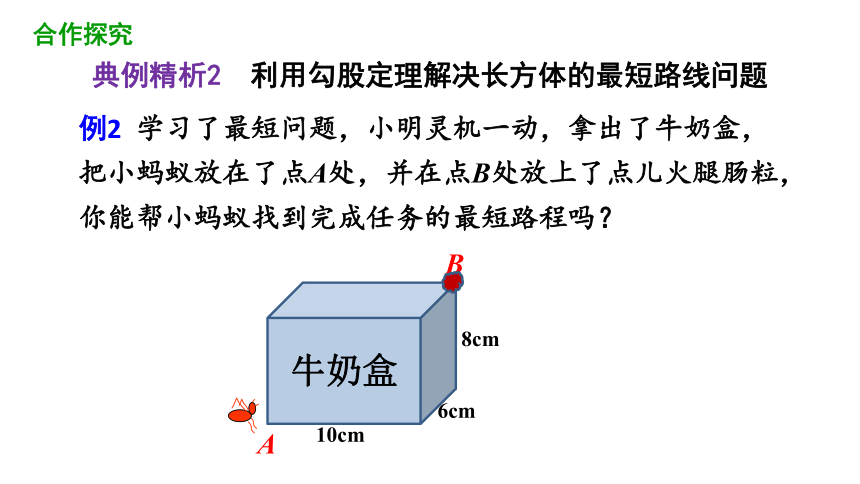
例2 学习了最短问题,小明灵机一动,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程吗?
6cm
8cm
10cm
典例精析2 利用勾股定理解决长方体的最短路线问题
合作探究
长
方
体
爬
行
路
径
A
B
F
E
H
G
A
B
C
D
E
F
G
H
前(后)
上(下)
A
B
C
D
E
F
G
H
B
C
G
F
E
H
A
B
C
D
E
F
G
H
右(左)
上(下)
前(后)
右(左)
B
C
A
E
F
G
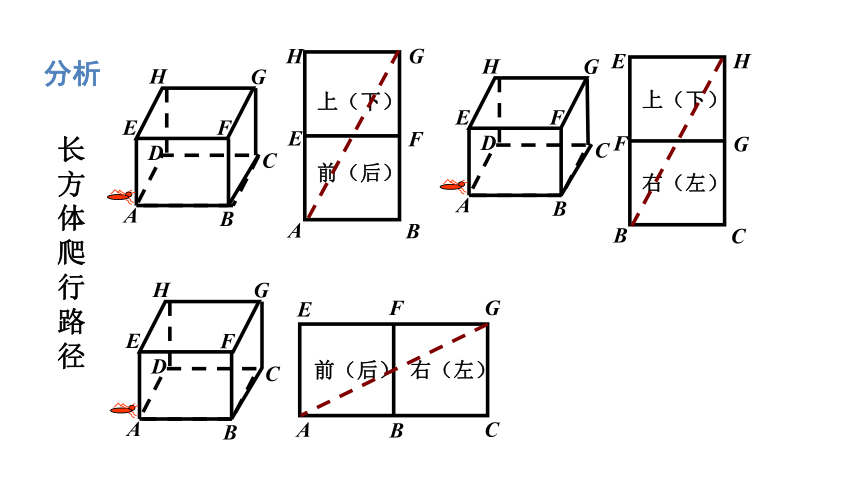
分析
B
B1
8
A
B2
6
10
B3
AB12=102 +(6+8)2=296
AB22= 82 +(10+6)2=320
AB32= 62 +(10+8)2=360
因为360>320>296
所以AB1 最短.
A
B
点A和点B分别是棱长为10cm的正方体盒子上相对的两点,一只蚂蚁在盒子表面由A处向B处爬行,所走最短路程的平方是多少?
前
上
A
B
A
B
左
上
A
B
前
右
巩固新知
A
B
C
解:如图所示
在Rt△ABC中,利用勾股定理可得,
AB 2=AC2+BC2
=20 2+102
=500
10
10
10
所以AB2=500.
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
解:连接对角线AC,只要分别量出AB、BC、AC的长度即可.
AB2+BC2=AC2
△ABC为直角三角形
新知二 利用勾股定理的逆定理解答实际问题
合作探究
(2)量得AD长是30 cm,AB长是40 cm,BD长是50 cm. AD边垂直于AB边吗?
解:AD2+AB2=302+402=502=BD2,
得∠DAB=90°,AD边垂直于AB边.
(3)若随身只有一个长度为20 cm的刻度尺,能有办法检验AD边是否垂直于AB边吗?
解:在AD上取点M,使AM=9,
在AB上取点N使AN=12,
测量MN是否是15,是,就是垂直;
不是,就是不垂直.
例 如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:因为AB=DC=8m,AD=BC=6m,
所以AB2+BC2=82+62=64+36=100.
又因为AC2=92=81,
所以AB2+BC2≠AC2,∠ABC≠90°,
所以该农民挖的不合格.
典例精析 利用勾股定理的逆定理解答测量问题
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为
x米,即AB=x米,而AC=2米,BC=1.5米,
有x2=1.52+22 ,x =2.5
故,最长是2.5+0.5=3(米)
答:这根铁棒的最长3米,最短2米.
故,最短是1.5+0.5=2(米)
当最短时:x =1.5
A
C
B
最短是多少米?
巩固新知
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.
故滑道AC的长度为5m.
解:设滑道AC的长度为x m,则AB的长也为x m,
AE的长度为(x-1)m.
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,
即(x-1)2+32=x2,
解得x=5.
例
新知三 利用勾股定理解答长度问题
合作探究
甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走.上午10:00,甲、乙两人相距多远?
解:如图:已知A 是甲、乙的出发点,10:00甲到达B 点,乙到达C 点.则:
AB=2×6=12(千米),
AC=1×5=5(千米).
在Rt△ABC 中,
所以BC =13(千米)
即甲乙两人相距13千米.
BC2=AC2+AB2 =52+122=169=132
巩固新知
解:连接BD.
在Rt△ABD中,由勾股定理得 BD2=AB2+AD2,
所以BD=5cm.又因为CD=12cm,BC=13cm,
所以BC2=CD2+BD2,所以△BDC是直角三角形.
所以S四边形ABCD=SRt△BCD-SRt△ABD=????????BD?CD-????????AB?AD
=???????? ×(5×12-3×4)=24 (cm2).
?
C
B
A
D
例 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
典例精析 利用勾股定理的逆定理解答面积问题
合作探究
如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解:因为S△ACD=30 cm2,DC=12 cm.
所以AC=5 cm.
又因为AB2+BC2=32+42=52=AC2,
所以△ABC是直角三角形, ∠B是直角.
所以
D
C
B
A
S△ACD=????????CD?AC=????????×12× AC=30( cm2 )
?
S△ABC=????????AB?BC=????????×3× 4=6( cm2 )
?
巩固新知
B
1.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中摆放方法正确的是 ( )
D
A. B.
C. D.
课堂练习
2.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300 m,公园到医院的距离为400 m,若公园到超市的距离为500 m,则公园在医院的 ( )
A.北偏东75°的方向上 B.北偏东65°的方向上
C.北偏东55°的方向上 D.无法确定
B
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:因为出发2小时,A组行了12×2=24(km),
B组行了9×2=18(km),
又因为A,B两组相距30km,
且有242+182=302,
所以A,B两组行进的方向成直角.
A
O
B
勾股定理及逆定理的应用
应用
最短路径问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题
解决不规则图形面积问题
测量问题
归纳新知
1.如图是一块长、宽、高分别是6 cm,4 cm和3 cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是( )
A.85 B.97 C.109 D.81
A
课后练习
5cm
3.如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,点A和点B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶面爬行到B点的最短路程是多少?
解:如图,应把台阶看成是纸片折成的,拉平(没高度)成一张长方形(长为3×3+2×3=15(dm),宽为20 dm)的纸.所以AB2=152+202=625(dm2).所以AB=25 dm,即蚂蚁沿着台阶面爬行到B点的最短路程是25 dm
4.一个圆柱形的油桶高120 cm,底面直径为50 cm,则桶内所能容下的最长的木棒长为( )
A.5 cm B.100 cm
C.120 cm D.130 cm
D
5.一有盖长方体笔盒长、宽、高分别为12 cm,6 cm,4 cm,则它能容纳的最长的笔的长度为( )
A.12 cm B.13 cm
C.14 cm D.15 cm
C
6.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口点A处出发先往东走8 km,又往北走2 km,遇到障碍后又往西走3 km,再折向北走到6 km处往东拐,仅走了1 km,就找到了宝藏,则门口点A到藏宝点的直线距离是( )
A.20 km B.14 km
C.11 km D.10 km
D
7.印度数学家什迦逻(1141年~1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.
解:如图,由题意知,AC=2,AD=0.5,在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=22-0.52=3.75.设湖水深BD为x尺,则BC为(x+0.5)尺.在Rt△BCD中,由勾股定理,得BD2+CD2=BC2,即x2+3.75=(x+0.5)2,解得x=3.5.答:湖水深3.5尺
D
9.(2019·西安月考)如图,长方体的透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼铒,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内到G处吃鱼铒,则小虫爬行的最短路线长为( )
A.40 cm B.60 cm C.80 cm D.100 cm
D
10.(2019·佛山期末)小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1 m,当他把绳子下端拉开5 m后,发现下端刚好接触地面,则旗杆高度为____m.
12
11.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶端A在AC上运动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑竿顶端A下滑多少米?
12.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6米,当秋千荡到AB1的位置时,下端B1距静止位置的水平距离EB1等于2.4米,距地面1.4米,求秋千AB的长.
解:设AB的长为x米,则AB1=x米,AE=AB+0.6-1.4=(x-0.8)米,在Rt△AB1E中,由勾股定理得AE2+B1E2=AB12,∴(x-0.8)2+2.42=x2,解得x=4,故秋千AB的长为4米
13.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°)放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=6 cm,BE=8 cm,求该三角形零件的面积.
再 见
第一章 勾股定理
1.3 勾股定理的应用
1.灵活会用勾股定理求解立体图形上两点之间的最短距离问题。
2.运用勾股定理及其逆定理解决简单的实际问题。
学习目标
在同一平面内,两点之间,线段最短
从行政楼A点走到教学楼B点怎样走最近?
教学楼
行政楼
B
A
你能说出这样走的理由吗?
导入新知
以小组为单位,研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题.
讨论 1.蚂蚁怎样沿圆柱体侧面从A点爬行到B点?
2.有最短路径吗?若有,哪条最短?你是怎样找到的?
B
A
我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!
新知一 利用勾股定理解答最短路径问题
合作探究
B
A
d
A
B
A'
A
B
B
A
O
想一想
蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
若已知圆柱体高为12 cm,底面周长为18 cm,则:
B
A
r
O
12
侧面展开图
12
18÷2
A
B
小结:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
A'
A'
AB2=122+(18÷2)2 所以AB=15.
例1 有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米?(已知油罐的底面半径是2m,高AB是5m,π取3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则AB'为梯子的最短距离.
因为AA'=2×3×2=12, A'B'=5m,
所以AB'=13m. 即梯子最短需13米.
典例精析1 利用勾股定理解决圆柱体的最短路线问题
数学思想:
立体图形
平面图形
转化
展开
如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)
3 勾股定理的应用
巩固新知
解:如图所示,将圆柱侧面沿AC剪开并展平,连接AB,则AB的长即为蜘蛛爬行的最短路程.
根据题意得AC=20 cm,BC=????????×2×π×5=15(cm).
在△ABC中,∠ACB=90°,由勾股定理得
AB2=BC2+AC2=152+202=252,
所以AB=25 cm,最短路程是25cm.
?
3 勾股定理的应用
B
牛奶盒
A
例2 学习了最短问题,小明灵机一动,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程吗?
6cm
8cm
10cm
典例精析2 利用勾股定理解决长方体的最短路线问题
合作探究
长
方
体
爬
行
路
径
A
B
F
E
H
G
A
B
C
D
E
F
G
H
前(后)
上(下)
A
B
C
D
E
F
G
H
B
C
G
F
E
H
A
B
C
D
E
F
G
H
右(左)
上(下)
前(后)
右(左)
B
C
A
E
F
G
分析
B
B1
8
A
B2
6
10
B3
AB12=102 +(6+8)2=296
AB22= 82 +(10+6)2=320
AB32= 62 +(10+8)2=360
因为360>320>296
所以AB1 最短.
A
B
点A和点B分别是棱长为10cm的正方体盒子上相对的两点,一只蚂蚁在盒子表面由A处向B处爬行,所走最短路程的平方是多少?
前
上
A
B
A
B
左
上
A
B
前
右
巩固新知
A
B
C
解:如图所示
在Rt△ABC中,利用勾股定理可得,
AB 2=AC2+BC2
=20 2+102
=500
10
10
10
所以AB2=500.
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
解:连接对角线AC,只要分别量出AB、BC、AC的长度即可.
AB2+BC2=AC2
△ABC为直角三角形
新知二 利用勾股定理的逆定理解答实际问题
合作探究
(2)量得AD长是30 cm,AB长是40 cm,BD长是50 cm. AD边垂直于AB边吗?
解:AD2+AB2=302+402=502=BD2,
得∠DAB=90°,AD边垂直于AB边.
(3)若随身只有一个长度为20 cm的刻度尺,能有办法检验AD边是否垂直于AB边吗?
解:在AD上取点M,使AM=9,
在AB上取点N使AN=12,
测量MN是否是15,是,就是垂直;
不是,就是不垂直.
例 如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:因为AB=DC=8m,AD=BC=6m,
所以AB2+BC2=82+62=64+36=100.
又因为AC2=92=81,
所以AB2+BC2≠AC2,∠ABC≠90°,
所以该农民挖的不合格.
典例精析 利用勾股定理的逆定理解答测量问题
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为
x米,即AB=x米,而AC=2米,BC=1.5米,
有x2=1.52+22 ,x =2.5
故,最长是2.5+0.5=3(米)
答:这根铁棒的最长3米,最短2米.
故,最短是1.5+0.5=2(米)
当最短时:x =1.5
A
C
B
最短是多少米?
巩固新知
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.
故滑道AC的长度为5m.
解:设滑道AC的长度为x m,则AB的长也为x m,
AE的长度为(x-1)m.
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,
即(x-1)2+32=x2,
解得x=5.
例
新知三 利用勾股定理解答长度问题
合作探究
甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走.上午10:00,甲、乙两人相距多远?
解:如图:已知A 是甲、乙的出发点,10:00甲到达B 点,乙到达C 点.则:
AB=2×6=12(千米),
AC=1×5=5(千米).
在Rt△ABC 中,
所以BC =13(千米)
即甲乙两人相距13千米.
BC2=AC2+AB2 =52+122=169=132
巩固新知
解:连接BD.
在Rt△ABD中,由勾股定理得 BD2=AB2+AD2,
所以BD=5cm.又因为CD=12cm,BC=13cm,
所以BC2=CD2+BD2,所以△BDC是直角三角形.
所以S四边形ABCD=SRt△BCD-SRt△ABD=????????BD?CD-????????AB?AD
=???????? ×(5×12-3×4)=24 (cm2).
?
C
B
A
D
例 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
典例精析 利用勾股定理的逆定理解答面积问题
合作探究
如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解:因为S△ACD=30 cm2,DC=12 cm.
所以AC=5 cm.
又因为AB2+BC2=32+42=52=AC2,
所以△ABC是直角三角形, ∠B是直角.
所以
D
C
B
A
S△ACD=????????CD?AC=????????×12× AC=30( cm2 )
?
S△ABC=????????AB?BC=????????×3× 4=6( cm2 )
?
巩固新知
B
1.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中摆放方法正确的是 ( )
D
A. B.
C. D.
课堂练习
2.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300 m,公园到医院的距离为400 m,若公园到超市的距离为500 m,则公园在医院的 ( )
A.北偏东75°的方向上 B.北偏东65°的方向上
C.北偏东55°的方向上 D.无法确定
B
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:因为出发2小时,A组行了12×2=24(km),
B组行了9×2=18(km),
又因为A,B两组相距30km,
且有242+182=302,
所以A,B两组行进的方向成直角.
A
O
B
勾股定理及逆定理的应用
应用
最短路径问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题
解决不规则图形面积问题
测量问题
归纳新知
1.如图是一块长、宽、高分别是6 cm,4 cm和3 cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长的平方是( )
A.85 B.97 C.109 D.81
A
课后练习
5cm
3.如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,点A和点B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶面爬行到B点的最短路程是多少?
解:如图,应把台阶看成是纸片折成的,拉平(没高度)成一张长方形(长为3×3+2×3=15(dm),宽为20 dm)的纸.所以AB2=152+202=625(dm2).所以AB=25 dm,即蚂蚁沿着台阶面爬行到B点的最短路程是25 dm
4.一个圆柱形的油桶高120 cm,底面直径为50 cm,则桶内所能容下的最长的木棒长为( )
A.5 cm B.100 cm
C.120 cm D.130 cm
D
5.一有盖长方体笔盒长、宽、高分别为12 cm,6 cm,4 cm,则它能容纳的最长的笔的长度为( )
A.12 cm B.13 cm
C.14 cm D.15 cm
C
6.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口点A处出发先往东走8 km,又往北走2 km,遇到障碍后又往西走3 km,再折向北走到6 km处往东拐,仅走了1 km,就找到了宝藏,则门口点A到藏宝点的直线距离是( )
A.20 km B.14 km
C.11 km D.10 km
D
7.印度数学家什迦逻(1141年~1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.
解:如图,由题意知,AC=2,AD=0.5,在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=22-0.52=3.75.设湖水深BD为x尺,则BC为(x+0.5)尺.在Rt△BCD中,由勾股定理,得BD2+CD2=BC2,即x2+3.75=(x+0.5)2,解得x=3.5.答:湖水深3.5尺
D
9.(2019·西安月考)如图,长方体的透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼铒,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内到G处吃鱼铒,则小虫爬行的最短路线长为( )
A.40 cm B.60 cm C.80 cm D.100 cm
D
10.(2019·佛山期末)小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1 m,当他把绳子下端拉开5 m后,发现下端刚好接触地面,则旗杆高度为____m.
12
11.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶端A在AC上运动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑竿顶端A下滑多少米?
12.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6米,当秋千荡到AB1的位置时,下端B1距静止位置的水平距离EB1等于2.4米,距地面1.4米,求秋千AB的长.
解:设AB的长为x米,则AB1=x米,AE=AB+0.6-1.4=(x-0.8)米,在Rt△AB1E中,由勾股定理得AE2+B1E2=AB12,∴(x-0.8)2+2.42=x2,解得x=4,故秋千AB的长为4米
13.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°)放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=6 cm,BE=8 cm,求该三角形零件的面积.
再 见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
