2.1认识无理数 同步课时训练 2021-2022学年八年级数学北师大版上册 (辽宁地区专用)(Word版含答案)
文档属性
| 名称 | 2.1认识无理数 同步课时训练 2021-2022学年八年级数学北师大版上册 (辽宁地区专用)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 14:54:07 | ||
图片预览




文档简介
同步课时训练-2021-2022学年八年级数学北师大版上册
(辽宁地区专用)
2.1无理数
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.下列各数中,是无理数的是( )
A.0
B.1.010
010
001
C.π
D.
2.下列说法中
无限小数是无理数;无理数是无限小数;无理数的平方一定是无理数;实数与数轴上的点是一一对应的,正确的个数S是(
)
A.1
B.2
C.3
D.4
3.公元前
5
世纪,毕达哥拉斯学派的一名成员希伯索斯发现了无理数.这个发现引发了数
学史上的第一次数学危机,打破了“万物皆数”的局限认识,迎来了数学的一次飞跃发展.
下面关于无理数的说法错误的是(
)
A.面积为
2
的正方形的边长是无理数
B.无限小数是无理数
C.无理数可以用数轴上的点来表示
D.半径为
1
的圆的周长是无理数
4.下列说法正确的有(
)
(1)有理数包括整数、分数和零;(2)不带根号的数都是有理数;(3)带根号的数都是无理数;(4)无理数都是无限小数;(5)无限小数都是无理数.
A.1
B.2
C.3
D.4
5.下列说法正确的是( )
A.所有无限小数都是无理数
B.所有无理数都是无限小数
C.有理数都是有限小数
D.不是有限小数的不是有理数
6.下列一组数:﹣8;2.7;;;0.66666…;0;2;0.080080008…(相邻两个8之间依次增加一个0)其中是无理数的有( )
A.0个
B.1个
C.2个
D.3个
7.下列命题是假命题的是(
)
A.所有的实数都可用数轴上的点表示;
B.同位角相等,两直线平行;
C.无理数包括正无理数,0,负无理数;
D.两点之间,线段最短.
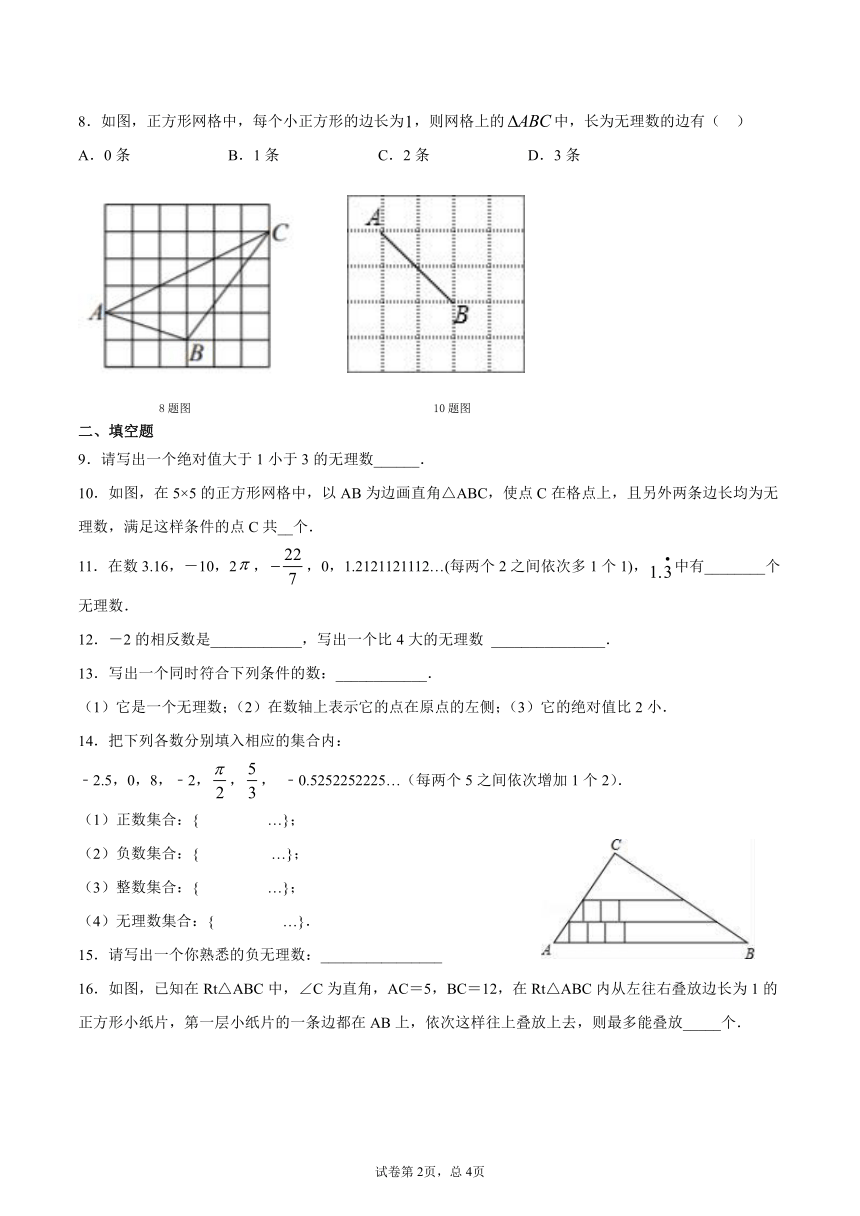
8.如图,正方形网格中,每个小正方形的边长为,则网格上的中,长为无理数的边有(
)
A.0条
B.1条
C.2条
D.3条
8题图
10题图
二、填空题
9.请写出一个绝对值大于1小于3的无理数______.
10.如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样条件的点C共__个.
11.在数3.16,-10,2,,0,1.2121121112…(每两个2之间依次多1个1),中有________个无理数.
12.-2的相反数是____________,写出一个比4大的无理数
_______________.
13.写出一个同时符合下列条件的数:____________.
(1)它是一个无理数;(2)在数轴上表示它的点在原点的左侧;(3)它的绝对值比2小.
14.把下列各数分别填入相应的集合内:
﹣2.5,0,8,﹣2,,,
﹣0.5252252225…(每两个5之间依次增加1个2).
(1)正数集合:{????????????????
…};
(2)负数集合:{?????????????????
…};
(3)整数集合:{????????????????
…};
(4)无理数集合:{????????????????
…}.
15.请写出一个你熟悉的负无理数:________________
16.如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放_____个.
三、解答题
17.无理数像一首读不完的长诗,既不循环,也不枯竭,无穷无尽,永葆常新,数学家称之为一种特殊的数.设面积为的圆的半径为x.
(1)x是有理数吗?说明理由.
(2)x的整数部分是多少?
(3)将x精确到十分位是多少?
18.把下列各数填入相应的集合中:-2,17,-3,+6,,0,32%,-,-0.6,2.101001000...,-(-42)
分数集合(
)
非负有理数集合(
)
整数集合(
)
无理数集合(
)
19.在下列网格中分别画出一个符合条件的直角三角形,要求三角形的顶点均在格点上,且满足:
(1)三边均为有理数;(2)其中只有一边为无理数.
20.阅读下列材料:
设:,①则.②
由,得,即.
所以.
根据上述提供的方法.把和化成分数,并想一想.是不是任何无限循环小数都可以化成分数?
21.有六个数:0.142
7,(-0.5)3,3.141
6,,-2π,0.102
002
000
2…,若无理数的个数为x,整数的个数为y,非负数的个数为z,求x+y+z的值.
22.已知在Rt△ABC中,∠C=90°,点A,B,C所对的边长分别为a,b,c.
(1)若,,求c的值,c是有理数吗?
(2)若,,求b的值,b是有理数吗?
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.C
【解析】
【思路点拨】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详细解答】解:A.0是整数,属于有理数;
B.1.010
010
001是有限小数,即分数,属于有理数;
C.π是无理数;
D.是分数,属于有理数;
故选:C.
【方法总结】此题主要考查了无理数的定义,熟练掌握是解题的关键.
2.B
【思路点拨】据无理数的定义和运算即可得到正确选项.
【详细解答】①无限不循环小数是无理数;错误;
②无理数是无限小数,正确;
③无理数的平方不一定是无理数;错误;
④实数与数轴上的点是一一对应的,正确.
故选B.
【方法总结】本题考查了无理数的定义及其运算,熟记无理数的定义是解题的关键.
3.B
【解析】
【思路点拨】根据无理数的概念解答即可.
【详细解答】A.
面积为
2
的正方形的边长为,是无理数
,正确;
B.
无限不循环小数是无理数,错误;C.
无理数可以用数轴上的点来表示,正确;
D.
半径为
1
的圆的周长是2π,是无理数,正确.故选B.
【方法总结】本题考查了无理数的概念,解题的关键是熟练掌握无理数的概念.
4.A
【思路点拨】根据有理数的分类,结合相关概念进行判断即可,整数包括正整数、负整数和0;分数包括正分数和负分数;有理数包括正有理数、负有理数和0;0不是正数也不是负数.
【详细解答】整数包含0,故错误;
Π不带根号,但是是无理数,错误;
例如能开方开的尽的是有理数,错误;
无理数都是无限不循环小数,都属于无限小数,正确;
无理数都是无限不循环小数,不是全部的无限小数,错误;
总共1个正确,故选A
【方法总结】考查有理数的概念,理解有理数的分类中各自的含义是解题的关键.
5.B
【解析】
【思路点拨】根据无理数的定义,以及无限小数的定义分析各选项即可作出判断.
【详细解答】解:A、
是无限小数,不是无理数,故A错误;
B、所有无理数都是无限小数,故B正确;
C、有理数5是整数,不是有限小数,故C错误;
D、有理数5是整数,不是有限小数,是有理数,故D错误.
故选:B.
【方法总结】本题考查了实数中无理数的定义,以及无限小数的定义,是基础题型,比较简单.
6.C
【详细解答】试题分析:无理数有:,0.080080008…(相邻两个8之间依次增加一个0).共2个.故选C.
考点:无理数.
7.C
【解析】试题解析:A、所有的实数都可用数轴上的点表示,所以A为真命题;
B、同位角相等,两直线平行,所以B为真命题;
C、无理数包括正无理数,负无理数,所以C为假命题;
D、两点之间,线段最短,所以D为真命题.
故选C.
8.C
【思路点拨】利用勾股定理计算出三边的长度即可.
【详细解答】解:;
;
;
∴的长是无理数,
故选:.
【方法总结】本题主要考查了勾股定理和无理数的识别,关键是牢记勾股定理的公式和无理数的定义.
9.(答案不唯一)
【思路点拨】结合题意,根据无理数和绝对值的性质分析,即可得到答案.
【详细解答】为无理数,且,
故答案为:(答案不唯一).
【方法总结】本题考查了无理数、绝对值的知识;解题的关键是熟练掌握无理数、绝对值的性质,从而完成求解.
10.4
【思路点拨】本题需根据直角三角形的定义和图形即可找出所有满足条件的点.
【详细解答】解:根据题意可得以AB为边画直角△ABC,使点C在格点上,且三边都为无理数,满足这样条件的点C共D,E,F,H4个点.
故答案为8.
11.2
【思路点拨】无理数的形式有:无限不循环小数,开方开不尽的数,π,据此逐个判断即可.
【详细解答】3.16是有限小数,属于有理数;-10是负整数,属于有理数;2π是无理数;是负分数,属于有理数;0是整数,属于有理数;1.2121121112…是无限不循环小数,属于无理数;是无限循环小数,属于有理数.无理数有2个.
【方法总结】本题考查实数的分类,熟记无理数的形式是关键.
12.2,
π+1(不唯一);
【思路点拨】根据一个数的相反数就是在这个数前面添上“-”号,求解即可;根据无理数的定义和已知写出符合的一个即可.
【详细解答】解:﹣2的相反数是2;比4大的无理数可以是π+1(不唯一).
故答案为:2;π+1(不唯一).
【方法总结】本题考查了相反数及无理数的概念,理解掌握相反数及无理数的概念是解题的关键.
13.-(不唯一)
【解析】
试题解析:符合上述三个条件.
故答案为:
(答案不唯一).
14.(1)正数集合:{8,,,,…};
(2)负数集合:{-2.5,-2
,-0.525225222…,…};
(3)整数集合:{0,8,-2
…};
(4)无理数集合:{
,-0.5252252225…,…}.
【解析】
试题分析:正数包括正有理数和正无理数,负数包括负有理数和负无理数,整数包括正整数、负整数和0,无理数是无限不循环小数.由此即可解决问题.
试题解析:
(1)正数集合:{8,,…};
(2)负数集合:{﹣2.5,﹣2,﹣0.5252252225…(每两个5之间依次增加1个2)…};
(3)整数集合:{0,8,﹣2,…};
(4)无理数集合:{,﹣0.5252252225…(每两个5之间依次增加1个2),…}.
15.
【解析】
由于开方开不尽的数或无限不循环小数是无理数,根据此定义即可解答.
解:例如-.(答案不唯一).
16.22个
【解析】
由勾股定理得:AB=.
由三角形的面积计算公式可知:△ABC的高=.
如图所示:根据题意有:△CAB∽△CEF,
∴,
∴EF=
,
∴第一层可放置10个小正方形纸片.
同法可得总共能放4层,依次可放置10、7、4、1个小正方形纸片,
∴最多能叠放10+7+4+1=22(个),
故答案为22个.
17.(1)x不是有理数;(2)x的整数部分是3;(3)将x精确到十分位为3.2.
【思路点拨】(1)根据圆的面积公式列式,再利用算术平方根的定义解答;
(2)根据无理数的大小估算计算即可得解;
(3)根据无理数的大小估算计算即可得解.
【详细解答】(1)x不是有理数.理由如下:
由圆的面积公式可得.
所以.
因为没有一个整数或分数的平方等于10,所以x不是有理数.
(2)由(1)知,
因为,,
所以,
所以x的整数部分是3.
(3)因为,,
所以.
又因为,,
所以,
所以将x精确到十分位为3.2.
【方法总结】本题考查了算术平方根以及无理数的大小估算,是基础题,熟记概念是解题的关键.
18.,32%,,-0.6;17,+6,0,32%,-(-42);17,-3,+6,0,-(-42);,2.101001000...
【思路点拨】按照有理数的分类填写.
【详细解答】解:分数集合{,32%,,-0.6,…};
非负有理数集合{17,+6,0,32%,-(-42),…}.
整数集合{17,-3,+6,0,-(-42),…}
无理数集合{,2.101001000...,…}
故答案为:,32%,,-0.6;17,+6,0,32%,-(-42);17,-3,+6,0,-(-42);,2.101001000...
【方法总结】本题考查了有理数以及证数和负数,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.
19.答案见解析
【思路点拨】(1)由勾股定理得出5,画出图形即可;
(2)由勾股定理得出直角边长为2、斜边长为的等腰直角三角形,画出图形即可.
【详细解答】(1)5,
△ABC即为所求,
如图1所示;
(2)由勾股定理得:
,
△DEF即为所求,
如图2所示.
【方法总结】本题考查了勾股定理、实数的定义;熟练掌握勾股定理,并能进行推理计算与作图是解决问题的关键.
20.,.任何无限循环小数都可以化成分数.
【解析】
【思路点拨】设①则,②;由,得;由已知,得,所以任何无限循环小数都可以这样化成分数.
【详细解答】解:设①则,②
由,得,即.
所以.
由已知,得,
所以.
任何无限循环小数都能化成分数.
【方法总结】考核知识点:无限循环小数和有理数.模仿,理解材料是关键.
21.x+y+z=6.
【思路点拨】由于无理数就是无限不循环小数.初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及0.1010010001…,等有这样规律的数,由此即可判定无理数x的值,根据整数的定义非负数的定义即可判定y、z的值,然后即可求解.
【详细解答】由题意得无理数有2个,所以x=2;整数有0个,所以y=0,非负数有4个,所以z=4,所以x+y+z=2+0+4=6.
【方法总结】本题主要考查实数的分类.无理数和有理数统称实数.有一定的综合性.
22.(1)有理数(2)不是有理数
【解析】
【思路点拨】根据勾股定理求出边长即可解答.
【详细解答】解:∵Rt△ABC中,∠C=90°,点A,B,C所对的边长分别为a,b,c,根据勾股定理得:
(1)c=
,c是有理数;
(2)b=
,b不是有理数.
【方法总结】本题考查勾股定理和有理数、无理数的定义,解题关键是熟练掌握勾股定理.
答案第1页,总2页
答案第1页,总2页
(辽宁地区专用)
2.1无理数
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.下列各数中,是无理数的是( )
A.0
B.1.010
010
001
C.π
D.
2.下列说法中
无限小数是无理数;无理数是无限小数;无理数的平方一定是无理数;实数与数轴上的点是一一对应的,正确的个数S是(
)
A.1
B.2
C.3
D.4
3.公元前
5
世纪,毕达哥拉斯学派的一名成员希伯索斯发现了无理数.这个发现引发了数
学史上的第一次数学危机,打破了“万物皆数”的局限认识,迎来了数学的一次飞跃发展.
下面关于无理数的说法错误的是(
)
A.面积为
2
的正方形的边长是无理数
B.无限小数是无理数
C.无理数可以用数轴上的点来表示
D.半径为
1
的圆的周长是无理数
4.下列说法正确的有(
)
(1)有理数包括整数、分数和零;(2)不带根号的数都是有理数;(3)带根号的数都是无理数;(4)无理数都是无限小数;(5)无限小数都是无理数.
A.1
B.2
C.3
D.4
5.下列说法正确的是( )
A.所有无限小数都是无理数
B.所有无理数都是无限小数
C.有理数都是有限小数
D.不是有限小数的不是有理数
6.下列一组数:﹣8;2.7;;;0.66666…;0;2;0.080080008…(相邻两个8之间依次增加一个0)其中是无理数的有( )
A.0个
B.1个
C.2个
D.3个
7.下列命题是假命题的是(
)
A.所有的实数都可用数轴上的点表示;
B.同位角相等,两直线平行;
C.无理数包括正无理数,0,负无理数;
D.两点之间,线段最短.
8.如图,正方形网格中,每个小正方形的边长为,则网格上的中,长为无理数的边有(
)
A.0条
B.1条
C.2条
D.3条
8题图
10题图
二、填空题
9.请写出一个绝对值大于1小于3的无理数______.
10.如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样条件的点C共__个.
11.在数3.16,-10,2,,0,1.2121121112…(每两个2之间依次多1个1),中有________个无理数.
12.-2的相反数是____________,写出一个比4大的无理数
_______________.
13.写出一个同时符合下列条件的数:____________.
(1)它是一个无理数;(2)在数轴上表示它的点在原点的左侧;(3)它的绝对值比2小.
14.把下列各数分别填入相应的集合内:
﹣2.5,0,8,﹣2,,,
﹣0.5252252225…(每两个5之间依次增加1个2).
(1)正数集合:{????????????????
…};
(2)负数集合:{?????????????????
…};
(3)整数集合:{????????????????
…};
(4)无理数集合:{????????????????
…}.
15.请写出一个你熟悉的负无理数:________________
16.如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放_____个.
三、解答题
17.无理数像一首读不完的长诗,既不循环,也不枯竭,无穷无尽,永葆常新,数学家称之为一种特殊的数.设面积为的圆的半径为x.
(1)x是有理数吗?说明理由.
(2)x的整数部分是多少?
(3)将x精确到十分位是多少?
18.把下列各数填入相应的集合中:-2,17,-3,+6,,0,32%,-,-0.6,2.101001000...,-(-42)
分数集合(
)
非负有理数集合(
)
整数集合(
)
无理数集合(
)
19.在下列网格中分别画出一个符合条件的直角三角形,要求三角形的顶点均在格点上,且满足:
(1)三边均为有理数;(2)其中只有一边为无理数.
20.阅读下列材料:
设:,①则.②
由,得,即.
所以.
根据上述提供的方法.把和化成分数,并想一想.是不是任何无限循环小数都可以化成分数?
21.有六个数:0.142
7,(-0.5)3,3.141
6,,-2π,0.102
002
000
2…,若无理数的个数为x,整数的个数为y,非负数的个数为z,求x+y+z的值.
22.已知在Rt△ABC中,∠C=90°,点A,B,C所对的边长分别为a,b,c.
(1)若,,求c的值,c是有理数吗?
(2)若,,求b的值,b是有理数吗?
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.C
【解析】
【思路点拨】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详细解答】解:A.0是整数,属于有理数;
B.1.010
010
001是有限小数,即分数,属于有理数;
C.π是无理数;
D.是分数,属于有理数;
故选:C.
【方法总结】此题主要考查了无理数的定义,熟练掌握是解题的关键.
2.B
【思路点拨】据无理数的定义和运算即可得到正确选项.
【详细解答】①无限不循环小数是无理数;错误;
②无理数是无限小数,正确;
③无理数的平方不一定是无理数;错误;
④实数与数轴上的点是一一对应的,正确.
故选B.
【方法总结】本题考查了无理数的定义及其运算,熟记无理数的定义是解题的关键.
3.B
【解析】
【思路点拨】根据无理数的概念解答即可.
【详细解答】A.
面积为
2
的正方形的边长为,是无理数
,正确;
B.
无限不循环小数是无理数,错误;C.
无理数可以用数轴上的点来表示,正确;
D.
半径为
1
的圆的周长是2π,是无理数,正确.故选B.
【方法总结】本题考查了无理数的概念,解题的关键是熟练掌握无理数的概念.
4.A
【思路点拨】根据有理数的分类,结合相关概念进行判断即可,整数包括正整数、负整数和0;分数包括正分数和负分数;有理数包括正有理数、负有理数和0;0不是正数也不是负数.
【详细解答】整数包含0,故错误;
Π不带根号,但是是无理数,错误;
例如能开方开的尽的是有理数,错误;
无理数都是无限不循环小数,都属于无限小数,正确;
无理数都是无限不循环小数,不是全部的无限小数,错误;
总共1个正确,故选A
【方法总结】考查有理数的概念,理解有理数的分类中各自的含义是解题的关键.
5.B
【解析】
【思路点拨】根据无理数的定义,以及无限小数的定义分析各选项即可作出判断.
【详细解答】解:A、
是无限小数,不是无理数,故A错误;
B、所有无理数都是无限小数,故B正确;
C、有理数5是整数,不是有限小数,故C错误;
D、有理数5是整数,不是有限小数,是有理数,故D错误.
故选:B.
【方法总结】本题考查了实数中无理数的定义,以及无限小数的定义,是基础题型,比较简单.
6.C
【详细解答】试题分析:无理数有:,0.080080008…(相邻两个8之间依次增加一个0).共2个.故选C.
考点:无理数.
7.C
【解析】试题解析:A、所有的实数都可用数轴上的点表示,所以A为真命题;
B、同位角相等,两直线平行,所以B为真命题;
C、无理数包括正无理数,负无理数,所以C为假命题;
D、两点之间,线段最短,所以D为真命题.
故选C.
8.C
【思路点拨】利用勾股定理计算出三边的长度即可.
【详细解答】解:;
;
;
∴的长是无理数,
故选:.
【方法总结】本题主要考查了勾股定理和无理数的识别,关键是牢记勾股定理的公式和无理数的定义.
9.(答案不唯一)
【思路点拨】结合题意,根据无理数和绝对值的性质分析,即可得到答案.
【详细解答】为无理数,且,
故答案为:(答案不唯一).
【方法总结】本题考查了无理数、绝对值的知识;解题的关键是熟练掌握无理数、绝对值的性质,从而完成求解.
10.4
【思路点拨】本题需根据直角三角形的定义和图形即可找出所有满足条件的点.
【详细解答】解:根据题意可得以AB为边画直角△ABC,使点C在格点上,且三边都为无理数,满足这样条件的点C共D,E,F,H4个点.
故答案为8.
11.2
【思路点拨】无理数的形式有:无限不循环小数,开方开不尽的数,π,据此逐个判断即可.
【详细解答】3.16是有限小数,属于有理数;-10是负整数,属于有理数;2π是无理数;是负分数,属于有理数;0是整数,属于有理数;1.2121121112…是无限不循环小数,属于无理数;是无限循环小数,属于有理数.无理数有2个.
【方法总结】本题考查实数的分类,熟记无理数的形式是关键.
12.2,
π+1(不唯一);
【思路点拨】根据一个数的相反数就是在这个数前面添上“-”号,求解即可;根据无理数的定义和已知写出符合的一个即可.
【详细解答】解:﹣2的相反数是2;比4大的无理数可以是π+1(不唯一).
故答案为:2;π+1(不唯一).
【方法总结】本题考查了相反数及无理数的概念,理解掌握相反数及无理数的概念是解题的关键.
13.-(不唯一)
【解析】
试题解析:符合上述三个条件.
故答案为:
(答案不唯一).
14.(1)正数集合:{8,,,,…};
(2)负数集合:{-2.5,-2
,-0.525225222…,…};
(3)整数集合:{0,8,-2
…};
(4)无理数集合:{
,-0.5252252225…,…}.
【解析】
试题分析:正数包括正有理数和正无理数,负数包括负有理数和负无理数,整数包括正整数、负整数和0,无理数是无限不循环小数.由此即可解决问题.
试题解析:
(1)正数集合:{8,,…};
(2)负数集合:{﹣2.5,﹣2,﹣0.5252252225…(每两个5之间依次增加1个2)…};
(3)整数集合:{0,8,﹣2,…};
(4)无理数集合:{,﹣0.5252252225…(每两个5之间依次增加1个2),…}.
15.
【解析】
由于开方开不尽的数或无限不循环小数是无理数,根据此定义即可解答.
解:例如-.(答案不唯一).
16.22个
【解析】
由勾股定理得:AB=.
由三角形的面积计算公式可知:△ABC的高=.
如图所示:根据题意有:△CAB∽△CEF,
∴,
∴EF=
,
∴第一层可放置10个小正方形纸片.
同法可得总共能放4层,依次可放置10、7、4、1个小正方形纸片,
∴最多能叠放10+7+4+1=22(个),
故答案为22个.
17.(1)x不是有理数;(2)x的整数部分是3;(3)将x精确到十分位为3.2.
【思路点拨】(1)根据圆的面积公式列式,再利用算术平方根的定义解答;
(2)根据无理数的大小估算计算即可得解;
(3)根据无理数的大小估算计算即可得解.
【详细解答】(1)x不是有理数.理由如下:
由圆的面积公式可得.
所以.
因为没有一个整数或分数的平方等于10,所以x不是有理数.
(2)由(1)知,
因为,,
所以,
所以x的整数部分是3.
(3)因为,,
所以.
又因为,,
所以,
所以将x精确到十分位为3.2.
【方法总结】本题考查了算术平方根以及无理数的大小估算,是基础题,熟记概念是解题的关键.
18.,32%,,-0.6;17,+6,0,32%,-(-42);17,-3,+6,0,-(-42);,2.101001000...
【思路点拨】按照有理数的分类填写.
【详细解答】解:分数集合{,32%,,-0.6,…};
非负有理数集合{17,+6,0,32%,-(-42),…}.
整数集合{17,-3,+6,0,-(-42),…}
无理数集合{,2.101001000...,…}
故答案为:,32%,,-0.6;17,+6,0,32%,-(-42);17,-3,+6,0,-(-42);,2.101001000...
【方法总结】本题考查了有理数以及证数和负数,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.
19.答案见解析
【思路点拨】(1)由勾股定理得出5,画出图形即可;
(2)由勾股定理得出直角边长为2、斜边长为的等腰直角三角形,画出图形即可.
【详细解答】(1)5,
△ABC即为所求,
如图1所示;
(2)由勾股定理得:
,
△DEF即为所求,
如图2所示.
【方法总结】本题考查了勾股定理、实数的定义;熟练掌握勾股定理,并能进行推理计算与作图是解决问题的关键.
20.,.任何无限循环小数都可以化成分数.
【解析】
【思路点拨】设①则,②;由,得;由已知,得,所以任何无限循环小数都可以这样化成分数.
【详细解答】解:设①则,②
由,得,即.
所以.
由已知,得,
所以.
任何无限循环小数都能化成分数.
【方法总结】考核知识点:无限循环小数和有理数.模仿,理解材料是关键.
21.x+y+z=6.
【思路点拨】由于无理数就是无限不循环小数.初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及0.1010010001…,等有这样规律的数,由此即可判定无理数x的值,根据整数的定义非负数的定义即可判定y、z的值,然后即可求解.
【详细解答】由题意得无理数有2个,所以x=2;整数有0个,所以y=0,非负数有4个,所以z=4,所以x+y+z=2+0+4=6.
【方法总结】本题主要考查实数的分类.无理数和有理数统称实数.有一定的综合性.
22.(1)有理数(2)不是有理数
【解析】
【思路点拨】根据勾股定理求出边长即可解答.
【详细解答】解:∵Rt△ABC中,∠C=90°,点A,B,C所对的边长分别为a,b,c,根据勾股定理得:
(1)c=
,c是有理数;
(2)b=
,b不是有理数.
【方法总结】本题考查勾股定理和有理数、无理数的定义,解题关键是熟练掌握勾股定理.
答案第1页,总2页
答案第1页,总2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
