平行四边形的判定2
图片预览




文档简介
(共28张PPT)
19.1.2 平行四边形的判定
(第2课时)
2、会综合运用平行四边形的四种判定方法和性质来证明问题.
1、掌握用一组对边平行且相等来判定平行四边形的方法.
3、理解三角形中位线的概念,掌握它的性质.
4、能较熟练地应用三角形中位线的性质进行有关的证明和计算.
到上一节课为止我们学习了几种判定平行四边形的方法?
2、两组对边分别相等的四边形是平行四边形
3、两组对角分别相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形
1、两组对边分别平行的四边形是平行四边形
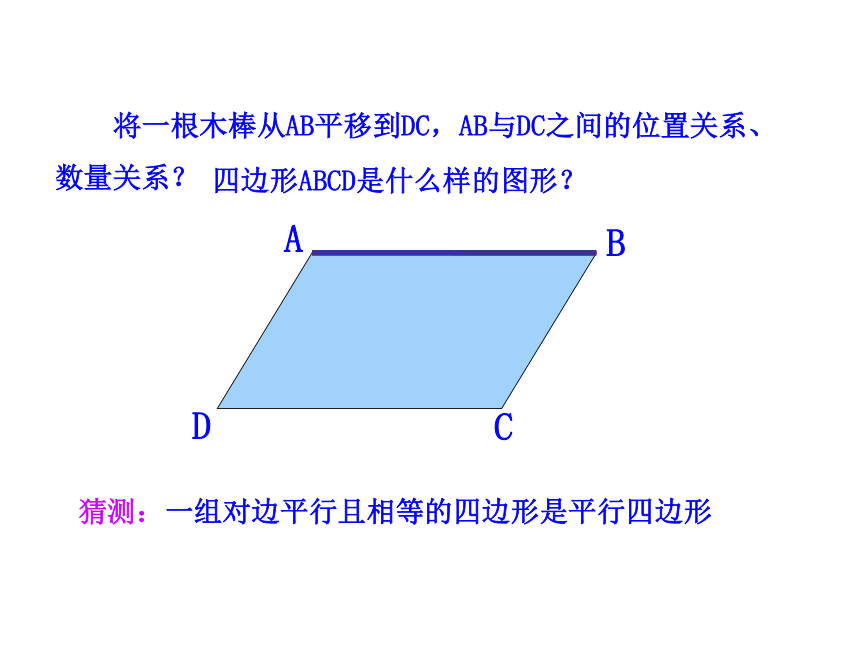
将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?
A
B
C
D
四边形ABCD是什么样的图形?
猜测:一组对边平行且相等的四边形是平行四边形
A
B
C
D
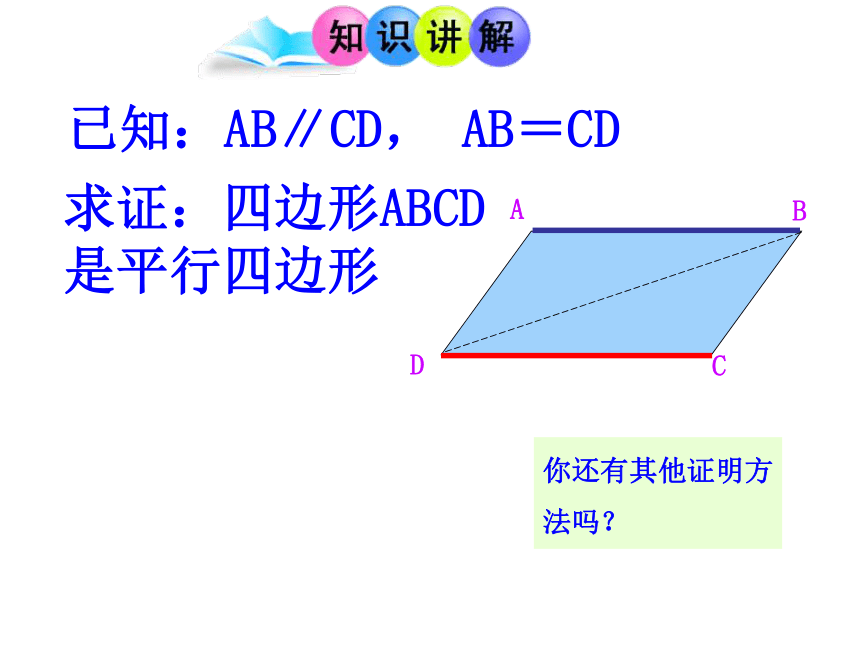
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
你还有其他证明方法吗?
判定定理
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
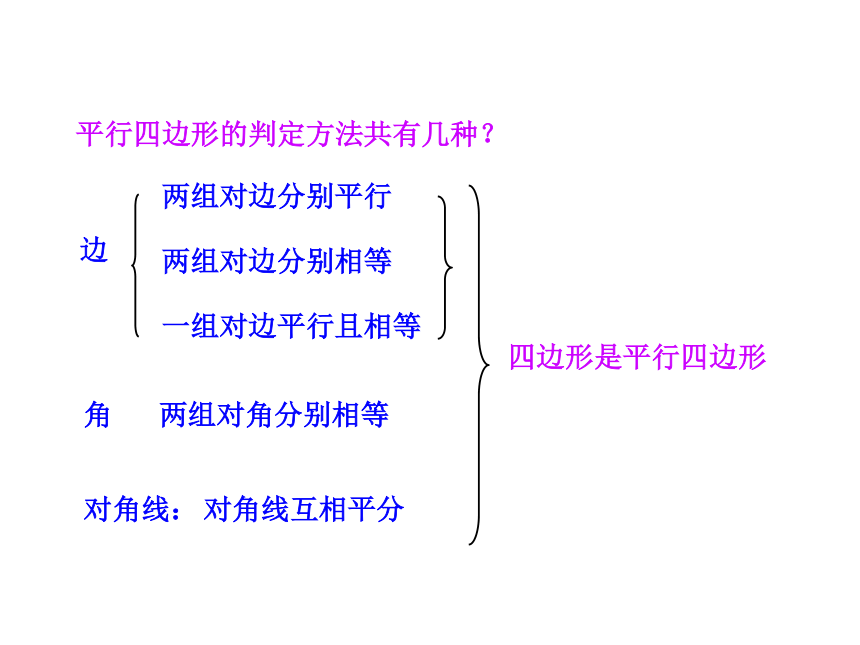
平行四边形的判定方法共有几种?
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
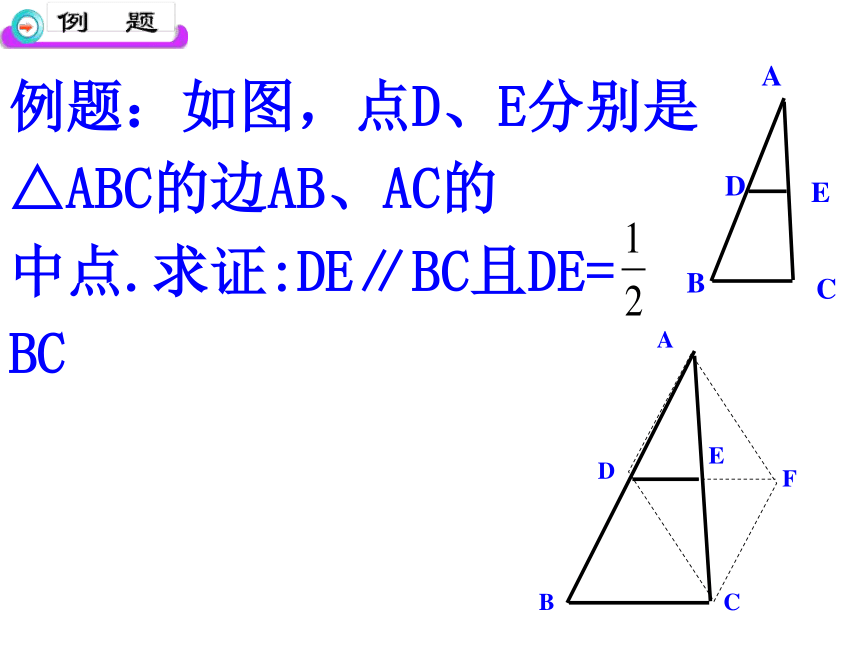
例题:如图,点D、E分别是△ABC的边AB、AC的
中点.求证:DE∥BC且DE= BC
A
B
C
D
E
B
C
A
D
E
F
定义:把连结三角形两边中点的线段叫做三角形的中位线.
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
中位线定理
1.①有一组对边平行的四边形是平行四边形.
②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形.
③对角线相等的四边形是平行四边形.
④一条对角线平分另一条对角线的四边形是平行四边形.
判断正误
2、如图, 四边形ABCD中,已知AB∥CD,那么再添加_________,使得四边形ABCD是一个平行四边形.
A
D
C
B
2.(2010·临沂中考)如图,在□ ABCD中,AC与BD相交于点O,点E是边BC的中点,AB=4,则OE的长( )
(A)2 (B)
(C)1 (D)
结
结
6. (2010·宿迁中考)如图,在□ ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.
【证明】∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形BEDF是平行四边形,
∴∠EBF=∠FDE.
7.(2010·中山中考)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知
∠BAC=30°,EF⊥AB,垂足为F,连结DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
【解析】(1)在Rt△ABC中,∠BAC=30°,
∴BC= AB,∴
在等边△ABE中,EF⊥AB,
∴
∴AC=EF.
(2)∵∠DAF=∠DAC+∠BAC=60°+30°=90°,∠EFA=90°
∴AD∥EF
又AC=AD=EF
∴四边形ADFE是平行四边形.
现有一块等腰直角三角形铁板,要求切割一次焊接成一个含有45°角的平行四边形 (不能有余料), 请你设计一种方案,并说明该方案正确的理由.
A
B
C
C
A
B
F
E
D
D
C
A
B
E
A
B
C
F
D
E
通过本课时的学习,需要我们
1、熟练掌握平行四边形的性质和判定并能灵活运用其解决相关的计算与证明.
2、理解三角形中位线的概念,掌握它的性质并能较熟练地应用三角形中位线的性质进行有关的证明和计算.
做人也要像蜡烛一样,在有限的一生中有一分热发一分光,给人以光明,给人以温暖。 —— 萧楚女
19.1.2 平行四边形的判定
(第2课时)
2、会综合运用平行四边形的四种判定方法和性质来证明问题.
1、掌握用一组对边平行且相等来判定平行四边形的方法.
3、理解三角形中位线的概念,掌握它的性质.
4、能较熟练地应用三角形中位线的性质进行有关的证明和计算.
到上一节课为止我们学习了几种判定平行四边形的方法?
2、两组对边分别相等的四边形是平行四边形
3、两组对角分别相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形
1、两组对边分别平行的四边形是平行四边形
将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?
A
B
C
D
四边形ABCD是什么样的图形?
猜测:一组对边平行且相等的四边形是平行四边形
A
B
C
D
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
你还有其他证明方法吗?
判定定理
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
平行四边形的判定方法共有几种?
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
例题:如图,点D、E分别是△ABC的边AB、AC的
中点.求证:DE∥BC且DE= BC
A
B
C
D
E
B
C
A
D
E
F
定义:把连结三角形两边中点的线段叫做三角形的中位线.
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
中位线定理
1.①有一组对边平行的四边形是平行四边形.
②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形.
③对角线相等的四边形是平行四边形.
④一条对角线平分另一条对角线的四边形是平行四边形.
判断正误
2、如图, 四边形ABCD中,已知AB∥CD,那么再添加_________,使得四边形ABCD是一个平行四边形.
A
D
C
B
2.(2010·临沂中考)如图,在□ ABCD中,AC与BD相交于点O,点E是边BC的中点,AB=4,则OE的长( )
(A)2 (B)
(C)1 (D)
结
结
6. (2010·宿迁中考)如图,在□ ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.
【证明】∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形BEDF是平行四边形,
∴∠EBF=∠FDE.
7.(2010·中山中考)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知
∠BAC=30°,EF⊥AB,垂足为F,连结DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
【解析】(1)在Rt△ABC中,∠BAC=30°,
∴BC= AB,∴
在等边△ABE中,EF⊥AB,
∴
∴AC=EF.
(2)∵∠DAF=∠DAC+∠BAC=60°+30°=90°,∠EFA=90°
∴AD∥EF
又AC=AD=EF
∴四边形ADFE是平行四边形.
现有一块等腰直角三角形铁板,要求切割一次焊接成一个含有45°角的平行四边形 (不能有余料), 请你设计一种方案,并说明该方案正确的理由.
A
B
C
C
A
B
F
E
D
D
C
A
B
E
A
B
C
F
D
E
通过本课时的学习,需要我们
1、熟练掌握平行四边形的性质和判定并能灵活运用其解决相关的计算与证明.
2、理解三角形中位线的概念,掌握它的性质并能较熟练地应用三角形中位线的性质进行有关的证明和计算.
做人也要像蜡烛一样,在有限的一生中有一分热发一分光,给人以光明,给人以温暖。 —— 萧楚女
