6.1.3 面积和体积公式教案-湘教版数学必修3
文档属性
| 名称 | 6.1.3 面积和体积公式教案-湘教版数学必修3 |
|
|
| 格式 | docx | ||
| 文件大小 | 192.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览


文档简介
6.1.3 表面积公式教案
教学目标:
1.通过对简单几何体侧面展开图探究,了解侧面积公式的由来.
2.准确掌握简单几何体的侧面积公式及推导方法.(难点)
3.会利用公式计算简单几何体的侧面积.(重点)
教学过程:
导入:长方形、平行四边形、梯形、三角形、圆……的面积如何求?
讲授新课:
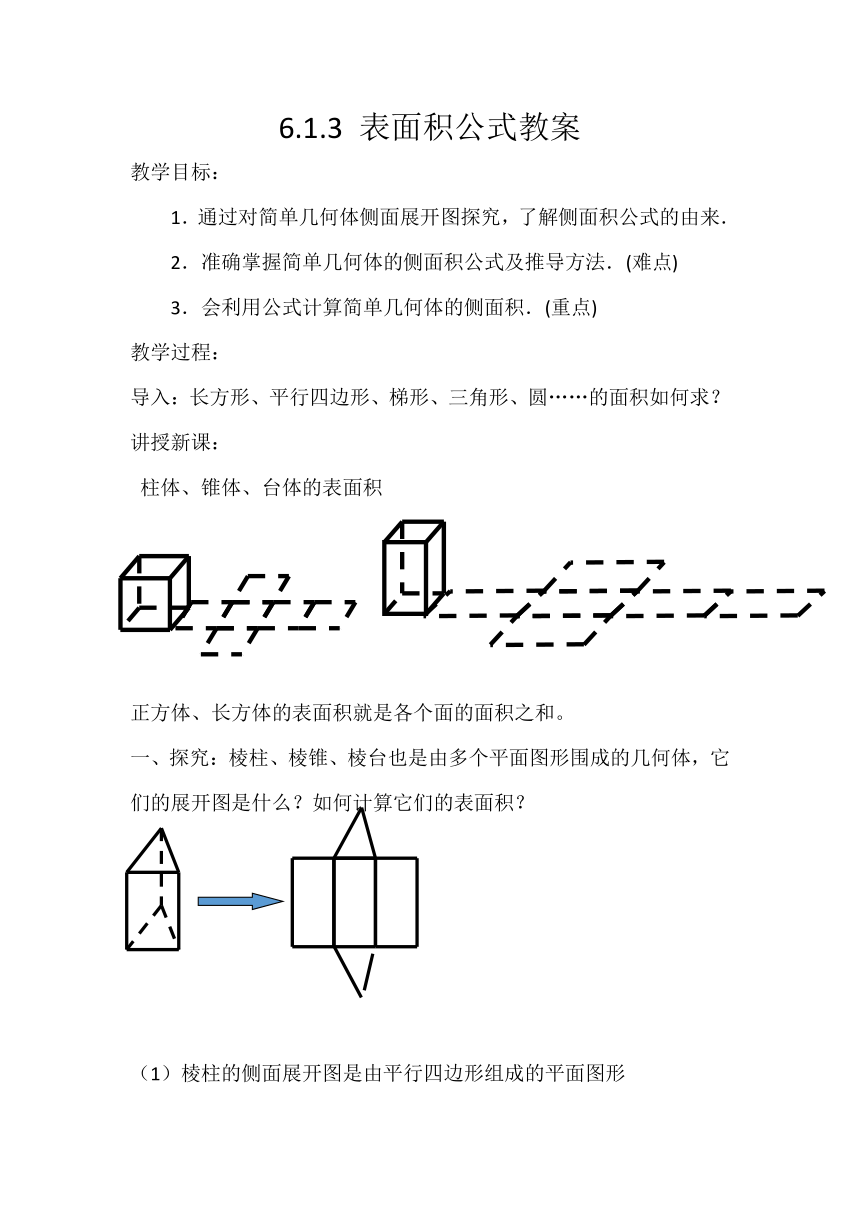
柱体、锥体、台体的表面积
2235835106680
400050189230-8445513335258064066675
正方体、长方体的表面积就是各个面的面积之和。
1426845639445一、探究:棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
600075600075-2921027940
(1)棱柱的侧面展开图是由平行四边形组成的平面图形
628650628650150431556515-133985104775
2235200272415(2)棱锥的侧面展开图是由三角形组成的平面图形
1247775474345-38100142875
(3)棱台的侧面展开图是由梯形组成的平面图形
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。
4080510412115S
B
A
C
S
B
A
C
例1、已知棱长为a,各面均为等边三角形的四面体S-ABC(如下图),求它的表面积。
解:
false
false
false
二、探究:圆柱、圆锥、圆台的表面积
(1)圆柱的侧面展开图是一个矩形:
如果圆柱的底面半径为 false ,母线为 false,那么圆柱的底面积为false,侧面积为false 。因此圆柱的表面积为
false
(2)圆锥的侧面展开图是一个扇形:
如果圆柱的底面半径为false,母线为false,那么圆锥的侧面积为:false
圆锥的表面积为:
false
(3)圆台的侧面展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即
false
证明:
false
360489561595false
false
false
false
思考:圆柱、圆锥、圆台的侧面积公式间的联系与区别-10795191770 S圆柱侧= 2πrl
S圆锥侧= πrl
S圆台侧=π(r1+r2)l
r1=0
r1=r2
S圆柱侧= 2πrl
S圆锥侧= πrl
S圆台侧=π(r1+r2)l
r1=0
r1=r2
(4)球的表面积
设球的半径为r,则表面积为:
false
4318000222250S
O
A
2
S
O
A
2
例2:已知一个圆锥的底面半径为2,高为false。求圆锥的侧面积。
例3:以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于( )
A.2π B.π C.2 D.1
练习:1、如图是一个几何体的三视图,其中正视图和左视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
A.6π B.12π C.18π D.24π
练习:2、如下图,一个圆台形花盆直径为20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm,那么花盆的表面积约是多少平方厘米(false取3.14,结果精确到1cm)?
351345513652515cm
10cm
7.5cm
15cm
10cm
7.5cm
小结:这节课你收获了什么?
作业:课本第21页练习题第1,2题
教学目标:
1.通过对简单几何体侧面展开图探究,了解侧面积公式的由来.
2.准确掌握简单几何体的侧面积公式及推导方法.(难点)
3.会利用公式计算简单几何体的侧面积.(重点)
教学过程:
导入:长方形、平行四边形、梯形、三角形、圆……的面积如何求?
讲授新课:
柱体、锥体、台体的表面积
2235835106680
400050189230-8445513335258064066675
正方体、长方体的表面积就是各个面的面积之和。
1426845639445一、探究:棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
600075600075-2921027940
(1)棱柱的侧面展开图是由平行四边形组成的平面图形
628650628650150431556515-133985104775
2235200272415(2)棱锥的侧面展开图是由三角形组成的平面图形
1247775474345-38100142875
(3)棱台的侧面展开图是由梯形组成的平面图形
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。
4080510412115S
B
A
C
S
B
A
C
例1、已知棱长为a,各面均为等边三角形的四面体S-ABC(如下图),求它的表面积。
解:
false
false
false
二、探究:圆柱、圆锥、圆台的表面积
(1)圆柱的侧面展开图是一个矩形:
如果圆柱的底面半径为 false ,母线为 false,那么圆柱的底面积为false,侧面积为false 。因此圆柱的表面积为
false
(2)圆锥的侧面展开图是一个扇形:
如果圆柱的底面半径为false,母线为false,那么圆锥的侧面积为:false
圆锥的表面积为:
false
(3)圆台的侧面展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即
false
证明:
false
360489561595false
false
false
false
思考:圆柱、圆锥、圆台的侧面积公式间的联系与区别-10795191770 S圆柱侧= 2πrl
S圆锥侧= πrl
S圆台侧=π(r1+r2)l
r1=0
r1=r2
S圆柱侧= 2πrl
S圆锥侧= πrl
S圆台侧=π(r1+r2)l
r1=0
r1=r2
(4)球的表面积
设球的半径为r,则表面积为:
false
4318000222250S
O
A
2
S
O
A
2
例2:已知一个圆锥的底面半径为2,高为false。求圆锥的侧面积。
例3:以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于( )
A.2π B.π C.2 D.1
练习:1、如图是一个几何体的三视图,其中正视图和左视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
A.6π B.12π C.18π D.24π
练习:2、如下图,一个圆台形花盆直径为20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm,那么花盆的表面积约是多少平方厘米(false取3.14,结果精确到1cm)?
351345513652515cm
10cm
7.5cm
15cm
10cm
7.5cm
小结:这节课你收获了什么?
作业:课本第21页练习题第1,2题
