6.2.1 点、线、面的位置关系教案-湘教版数学必修3
文档属性
| 名称 | 6.2.1 点、线、面的位置关系教案-湘教版数学必修3 |
|
|
| 格式 | docx | ||
| 文件大小 | 202.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览

文档简介
点、线、面位置关系(第二课时)
教学目标:
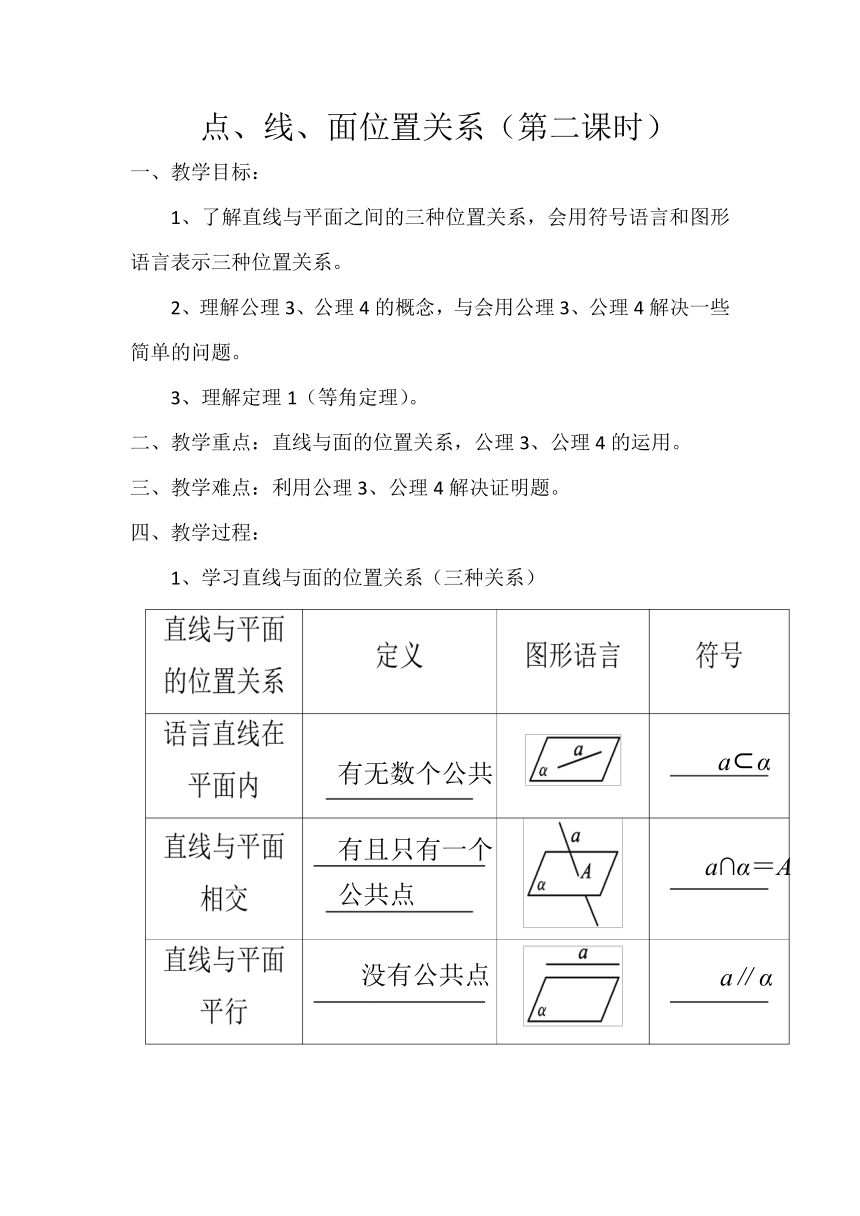
1、了解直线与平面之间的三种位置关系,会用符号语言和图形语言表示三种位置关系。
2、理解公理3、公理4的概念,与会用公理3、公理4解决一些简单的问题。
3、理解定理1(等角定理)。
二、教学重点:直线与面的位置关系,公理3、公理4的运用。
三、教学难点:利用公理3、公理4解决证明题。
四、教学过程:
1、学习直线与面的位置关系(三种关系)
a∥α
a∩α=A
a?α
没有公共点
有且只有一个
公共点
有无数个公共点
\* MERGEFORMAT
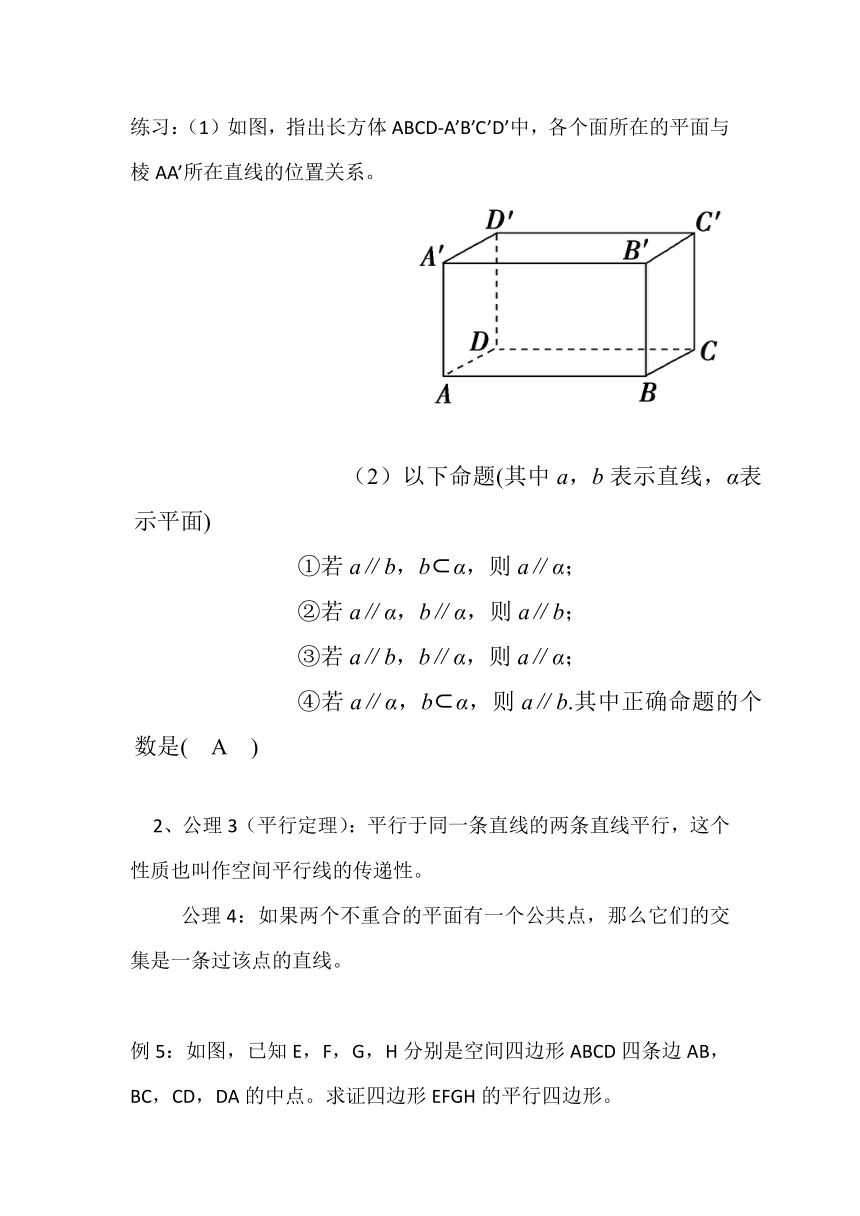
练习:(1)如图,指出长方体ABCD-A’B’C’D’中,各个面所在的平面与棱AA’所在直线的位置关系。
(2)以下命题(其中a,b表示直线,α表示平面)
①若a∥b,b?α,则a∥α;
②若a∥α,b∥α,则a∥b;
③若a∥b,b∥α,则a∥α;
④若a∥α,b?α,则a∥b.其中正确命题的个数是( A )
A.0个 B.1个
C.2个 D.3个
2、公理3(平行定理):平行于同一条直线的两条直线平行,这个性质也叫作空间平行线的传递性。
公理4:如果两个不重合的平面有一个公共点,那么它们的交集是一条过该点的直线。
例5:如图,已知E,F,G,H分别是空间四边形ABCD四条边AB,BC,CD,DA的中点。求证四边形EFGH的平行四边形。
E
A
H
B
D
C
F
G
练习:已知棱长为a的正方体ABCD-A′B′C′D′中,M,N分别为CD、AD的中点.求证:四边形MNA′C′是梯形.
定理1(等角定理):空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补。
\* MERGEFORMAT
练习:如图所示,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点,求证:∠C1E1B1=∠CEB.
课堂小结:
1、直线与平面的位置关系有且只有三种:
直线在平面内、直线与平面相交、直线与平面平行.
如何利用公理3、公理4解决问题。
等角定理的应用。
教学目标:
1、了解直线与平面之间的三种位置关系,会用符号语言和图形语言表示三种位置关系。
2、理解公理3、公理4的概念,与会用公理3、公理4解决一些简单的问题。
3、理解定理1(等角定理)。
二、教学重点:直线与面的位置关系,公理3、公理4的运用。
三、教学难点:利用公理3、公理4解决证明题。
四、教学过程:
1、学习直线与面的位置关系(三种关系)
a∥α
a∩α=A
a?α
没有公共点
有且只有一个
公共点
有无数个公共点
\* MERGEFORMAT
练习:(1)如图,指出长方体ABCD-A’B’C’D’中,各个面所在的平面与棱AA’所在直线的位置关系。
(2)以下命题(其中a,b表示直线,α表示平面)
①若a∥b,b?α,则a∥α;
②若a∥α,b∥α,则a∥b;
③若a∥b,b∥α,则a∥α;
④若a∥α,b?α,则a∥b.其中正确命题的个数是( A )
A.0个 B.1个
C.2个 D.3个
2、公理3(平行定理):平行于同一条直线的两条直线平行,这个性质也叫作空间平行线的传递性。
公理4:如果两个不重合的平面有一个公共点,那么它们的交集是一条过该点的直线。
例5:如图,已知E,F,G,H分别是空间四边形ABCD四条边AB,BC,CD,DA的中点。求证四边形EFGH的平行四边形。
E
A
H
B
D
C
F
G
练习:已知棱长为a的正方体ABCD-A′B′C′D′中,M,N分别为CD、AD的中点.求证:四边形MNA′C′是梯形.
定理1(等角定理):空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补。
\* MERGEFORMAT
练习:如图所示,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点,求证:∠C1E1B1=∠CEB.
课堂小结:
1、直线与平面的位置关系有且只有三种:
直线在平面内、直线与平面相交、直线与平面平行.
如何利用公理3、公理4解决问题。
等角定理的应用。
