2021-2022学年沪科新版九年级上册数学第22章 相似形单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年沪科新版九年级上册数学第22章 相似形单元测试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 376.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览

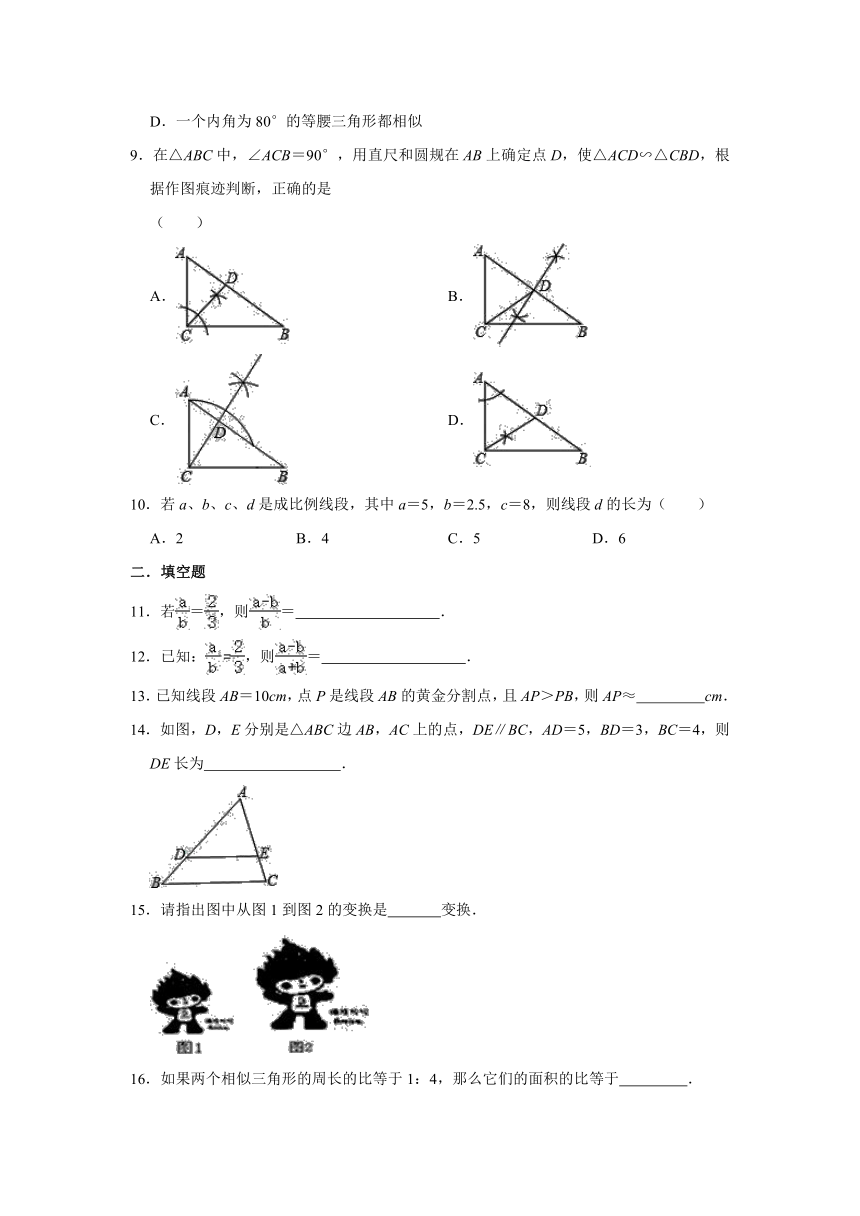
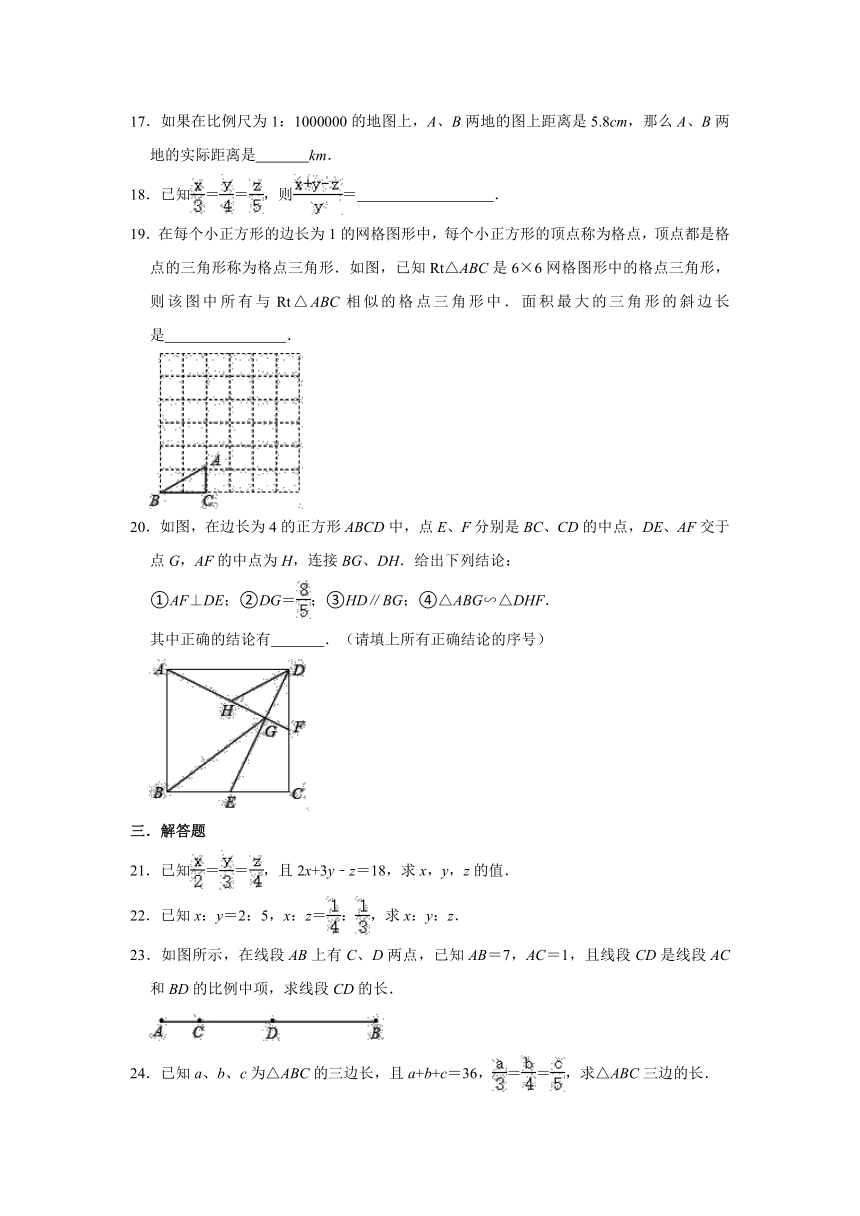
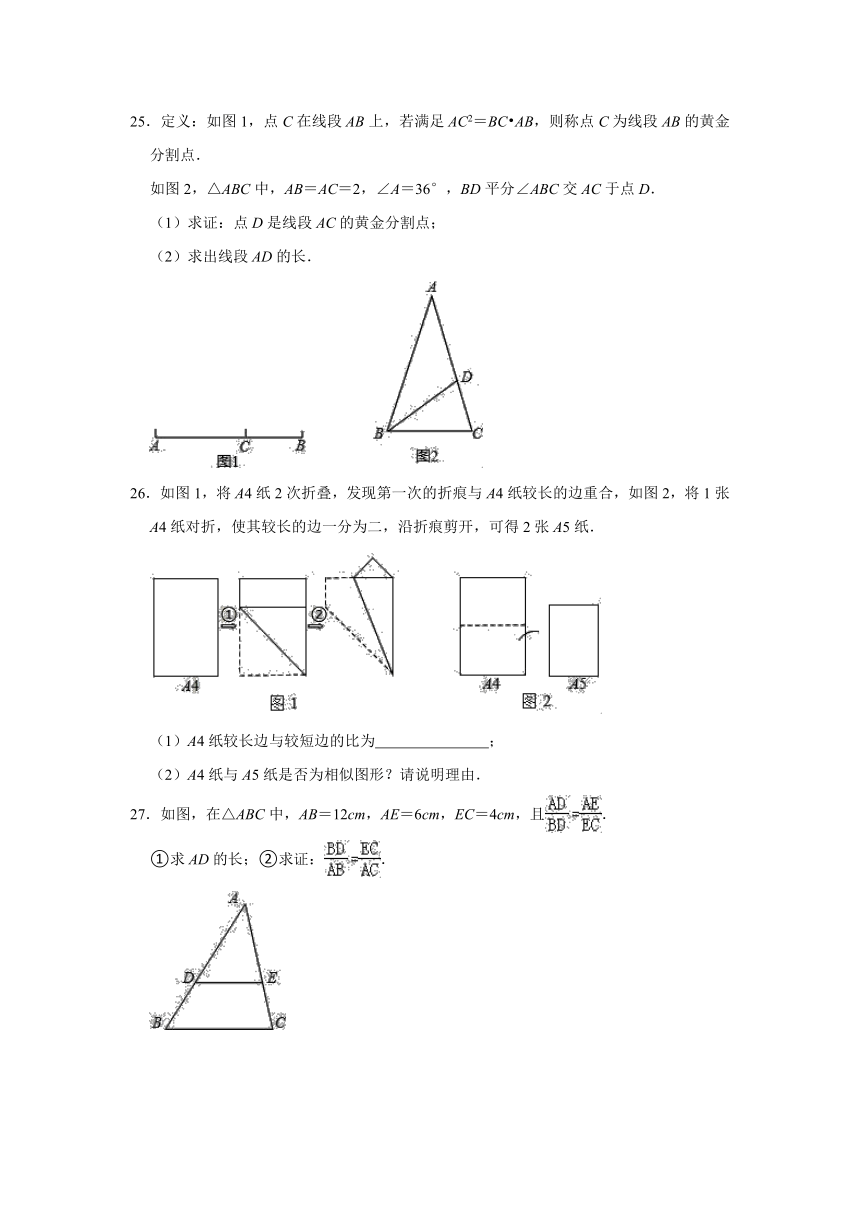

文档简介
2021-2022学年沪科新版九年级上册数学《第22章
相似形》单元测试卷
一.选择题
1.若3x﹣4y=0,则的值是( )
A.
B.
C.
D.
2.若,则的值是( )
A.1
B.2
C.3
D.4
3.已知=,那么的值为( )
A.
B.
C.
D.
4.已知点C是线段AB的黄金分割点(AC>BC),AB=4,则线段AC的长是( )
A.
B.
C.
D.
5.下列各组图形一定相似的是( )
A.有一个角相等的等腰三角形
B.有一个角相等的直角三角形
C.有一个角是100°的等腰三角形
D.有一个角是对顶角的两个三角形
6.若△ABC∽△DEF,=2,△ABC面积为8,则△DEF的面积为( )
A.1
B.2
C.4
D.8
7.如图,已知AB∥CD∥EF,BD:DF=1:2,那么下列结论中,正确的是( )
A.AC:AE=1:3
B.CE:EA=1:3
C.CD:EF=1:2
D.AB:EF=1:2
8.下列说法正确的是( )
A.菱形都相似
B.正六边形都相似
C.矩形都相似
D.一个内角为80°的等腰三角形都相似
9.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是
( )
A.
B.
C.
D.
10.若a、b、c、d是成比例线段,其中a=5,b=2.5,c=8,则线段d的长为( )
A.2
B.4
C.5
D.6
二.填空题
11.若=,则=
.
12.已知:,则=
.
13.已知线段AB=10cm,点P是线段AB的黄金分割点,且AP>PB,则AP≈
cm.
14.如图,D,E分别是△ABC边AB,AC上的点,DE∥BC,AD=5,BD=3,BC=4,则DE长为
.
15.请指出图中从图1到图2的变换是
变换.
16.如果两个相似三角形的周长的比等于1:4,那么它们的面积的比等于
.
17.如果在比例尺为1:1000000的地图上,A、B两地的图上距离是5.8cm,那么A、B两地的实际距离是
km.
18.已知==,则=
.
19.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是
.
20.如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点,DE、AF交于点G,AF的中点为H,连接BG、DH.给出下列结论:
①AF⊥DE;②DG=;③HD∥BG;④△ABG∽△DHF.
其中正确的结论有
.(请填上所有正确结论的序号)
三.解答题
21.已知==,且2x+3y﹣z=18,求x,y,z的值.
22.已知x:y=2:5,x:z=:,求x:y:z.
23.如图所示,在线段AB上有C、D两点,已知AB=7,AC=1,且线段CD是线段AC和BD的比例中项,求线段CD的长.
24.已知a、b、c为△ABC的三边长,且a+b+c=36,==,求△ABC三边的长.
25.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
26.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为
;
(2)A4纸与A5纸是否为相似图形?请说明理由.
27.如图,在△ABC中,AB=12cm,AE=6cm,EC=4cm,且.
①求AD的长;②求证:.
参考答案与试题解析
一.选择题
1.解:由3x﹣4y=0,得
x=,
∴==,
故选:B.
2.解:设=k,则x=2k,y=7k,z=5k,
把x=2k,y=7k,z=5k代入,
故选:B.
3.解:∵=,
∴设a=2k,则b=3k,
则原式==.
故选:B.
4.解:根据题意得AC=AB=×4=2﹣2.
故选:A.
5.解:A.若一个等腰三角形的底角和一个等腰三角形的顶角相等,无法判定两三角形相似,故本选项错误;
B.两个直角三角形中直角相等,则两锐角的大小无法确定,无法判定两三角形相似,故本选项错误;
C.一个角为100°,则这个角必须是顶角,且两底角度数为40°,故两个三角形三内角均相等,即可判定两三角形相似,故本选项正确;
D.对顶角相等的三角形中,其他两个角的度数不确定,故无法判定两三角形相似,故本选项错误,
故选:C.
6.解:∵△ABC∽△DEF,=2,
∴=4.
∵△ABC面积为8,
∴△DEF的面积==2.
故选:B.
7.解:∵AB∥CD∥EF,BD:DF=1:2,
∴AC:AE=1:3,故A选项正确;
CE:EA=2:3,故B选项错误;
CD:EF的值无法确定,故C选项错误;
AB:EF的值无法确定,故D选项错误;
故选:A.
8.解:A、所有的菱形,边长相等,所以对应边成比例,角不一定对应相等,所以不一定都相似,故本选项错误;
B、所有的正六边形,边长相等,所以对应边成比例,角都是120°,相等,所以都相似,故本选项正确;
C、所有的矩形,对应角的度数一定相同,但对应边的比值不一定相等,故本选项错误;
D、一个内角为80°的等腰三角形可能是顶角80°也可能是底角是80°,无法判断,此选项错误;
故选:B.
9.解:当CD是AB的垂线时,△ACD∽△CBD.
∵CD⊥AB,
∴∠CDA=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的角平分线,不符合题意;
B选项中,CD不与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不与AB垂直,不符合题意;
故选:C.
10.解:因为a、b、c、d是成比例线段,
可得:,
解得:d=4,
故选:B.
二.填空题
11.解:∵=,
∴a=b,
则==﹣.
故答案为:﹣.
12.解:∵=,
∴设a=2k,b=3k,
∴==﹣,
故答案为:﹣.
13.解:∵点P是线段AB的黄金分割点,且AP>PB,AB=10cm,
∴AP=AB≈6.18(cm).
故答案为6.18.
14.解:∵DE∥BC
∴,
∴=,
∴DE=,
故答案为:.
15.解:∵从图1到图2,图形形状没变,只是大小发生改变,
∴从图1到图2的变换是相似变换.
故答案为:相似,
16.解:∵两个相似三角形的周长的比等于1:4,
∴它们的相似比为1:4,
∴它们的面积的比等于1:16.
故答案为:1:16.
17.解:根据题意,5.8÷=5800000(厘米)=58(千米).
即实际距离是58千米.
故答案为:58.
18.解:设===a,
x=3a,y=4a,z=5a.
==,
故答案为:.
19.解:∵在Rt△ABC中,AC=1,BC=2,
∴AB=,AC:BC=1:2,
∴与Rt△ABC相似的格点三角形的两直角边的比值为1:2,
若该三角形最短边长为4,则另一直角边长为8,但在6×6网格图形中,最长线段为6,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出DE=,EF=2,DF=5的三角形,
∵===,
∴△ABC∽△DFE,
∴∠DEF=∠C=90°,
∴此时△DEF的面积为:×2÷2=10,△DEF为面积最大的三角形,其斜边长为:5.
故答案为:5.
20.解:∵四边形ABCD为正方形,
∴∠ADC=∠BCD=90°,AD=CD,
∵E和F分别为BC和CD中点,
∴DF=EC=2,
∴△ADF≌△DCE(SAS),
∴∠AFD=∠DEC,∠FAD=∠EDC,
∵∠EDC+∠DEC=90°,
∴∠EDC+∠AFD=90°,
∴∠DGF=90°,即DE⊥AF,故①正确;
∵AD=4,DF=CD=2,
∴AF=,
∴DG=AD×DF÷AF=,故②错误;
∵H为AF中点,
∴HD=HF=AF=,
∴∠HDF=∠HFD,
∵AB∥DC,
∴∠HDF=∠HFD=∠BAG,
∵AG==,AB=4,
∴,
∴△ABG~△DHF,故④正确;
∴∠ABG=∠DHF,而AB≠AG,
则∠ABG和∠AGB不相等,
故∠AGB≠∠DHF,
故HD与BG不平行,故③错误;
故答案为:①④.
三.解答题
21.解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
22.解:∵x:y=2:5,x:z=:=3:4,
∴x:y=6:15,x:z=6:8,
∴x:y:z=6:15:8.
23.解:∵AB=7,AC=1,
∴BD=AB﹣AC﹣CD=6﹣CD,
∵线段CD是线段AC和BD的比例中项,
∴CD2=AC?BD,
即CD2=1×(6﹣CD),
解得:CD=2.
24.解:==,得
a=c,b=c,
把a=c,b=c代入且a+b+c=36,得
c+c+c=36,
解得c=15,
a=c=9,
b=c=12,
△ABC三边的长:a=9,b=12,c=15.
25.解:(1)∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABD=36°,∠BDC=72°,
∴AD=BD,BC=BD,
∴△ABC∽△BDC,
∴=,即=,
∴AD2=AC?CD.
∴点D是线段AC的黄金分割点.
(2)∵点D是线段AC的黄金分割点,
∴AD=AC,
∵AC=2,
∴AD=﹣1.
26.解:(1)如图1,
由折叠过程可以看到:第一次折叠,A与D重合,四边形ABDC为正方形,折痕BC为对角线,由勾股定理可得BC=AB;第二次折叠,第一次的折痕与A4纸较长的边重合,即BC与较长边重合.所以,较长边=AB.
∴A4纸较长边与较短边的比为:.
故答案为:.
(2)A4纸与A5纸是相似图形.理由:
∵A4纸较长边与较短边的比为:,
∴设A4纸较短边的长为a,则较长边为a.
∵由图2可知:A5纸的长边与A4纸的短边重合,短边等于A4纸的长边的一半,
∴A5纸的长边为a,短边为.
∴A5纸的长边与短边的比为:=.
∴A4纸较长边与较短边的比=A5纸的长边与短边的比.
又∵A4纸与A5纸的四个角均为直角,
∴A4纸与A5纸相似.
27.解:①设AD=xcm,则BD=AB﹣AD=(12﹣x)cm
∵,
∴
解得x=7.2cm
∴AD=7.2cm;
②∵,
∴
即.
∴.
相似形》单元测试卷
一.选择题
1.若3x﹣4y=0,则的值是( )
A.
B.
C.
D.
2.若,则的值是( )
A.1
B.2
C.3
D.4
3.已知=,那么的值为( )
A.
B.
C.
D.
4.已知点C是线段AB的黄金分割点(AC>BC),AB=4,则线段AC的长是( )
A.
B.
C.
D.
5.下列各组图形一定相似的是( )
A.有一个角相等的等腰三角形
B.有一个角相等的直角三角形
C.有一个角是100°的等腰三角形
D.有一个角是对顶角的两个三角形
6.若△ABC∽△DEF,=2,△ABC面积为8,则△DEF的面积为( )
A.1
B.2
C.4
D.8
7.如图,已知AB∥CD∥EF,BD:DF=1:2,那么下列结论中,正确的是( )
A.AC:AE=1:3
B.CE:EA=1:3
C.CD:EF=1:2
D.AB:EF=1:2
8.下列说法正确的是( )
A.菱形都相似
B.正六边形都相似
C.矩形都相似
D.一个内角为80°的等腰三角形都相似
9.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是
( )
A.
B.
C.
D.
10.若a、b、c、d是成比例线段,其中a=5,b=2.5,c=8,则线段d的长为( )
A.2
B.4
C.5
D.6
二.填空题
11.若=,则=
.
12.已知:,则=
.
13.已知线段AB=10cm,点P是线段AB的黄金分割点,且AP>PB,则AP≈
cm.
14.如图,D,E分别是△ABC边AB,AC上的点,DE∥BC,AD=5,BD=3,BC=4,则DE长为
.
15.请指出图中从图1到图2的变换是
变换.
16.如果两个相似三角形的周长的比等于1:4,那么它们的面积的比等于
.
17.如果在比例尺为1:1000000的地图上,A、B两地的图上距离是5.8cm,那么A、B两地的实际距离是
km.
18.已知==,则=
.
19.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是
.
20.如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点,DE、AF交于点G,AF的中点为H,连接BG、DH.给出下列结论:
①AF⊥DE;②DG=;③HD∥BG;④△ABG∽△DHF.
其中正确的结论有
.(请填上所有正确结论的序号)
三.解答题
21.已知==,且2x+3y﹣z=18,求x,y,z的值.
22.已知x:y=2:5,x:z=:,求x:y:z.
23.如图所示,在线段AB上有C、D两点,已知AB=7,AC=1,且线段CD是线段AC和BD的比例中项,求线段CD的长.
24.已知a、b、c为△ABC的三边长,且a+b+c=36,==,求△ABC三边的长.
25.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
26.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为
;
(2)A4纸与A5纸是否为相似图形?请说明理由.
27.如图,在△ABC中,AB=12cm,AE=6cm,EC=4cm,且.
①求AD的长;②求证:.
参考答案与试题解析
一.选择题
1.解:由3x﹣4y=0,得
x=,
∴==,
故选:B.
2.解:设=k,则x=2k,y=7k,z=5k,
把x=2k,y=7k,z=5k代入,
故选:B.
3.解:∵=,
∴设a=2k,则b=3k,
则原式==.
故选:B.
4.解:根据题意得AC=AB=×4=2﹣2.
故选:A.
5.解:A.若一个等腰三角形的底角和一个等腰三角形的顶角相等,无法判定两三角形相似,故本选项错误;
B.两个直角三角形中直角相等,则两锐角的大小无法确定,无法判定两三角形相似,故本选项错误;
C.一个角为100°,则这个角必须是顶角,且两底角度数为40°,故两个三角形三内角均相等,即可判定两三角形相似,故本选项正确;
D.对顶角相等的三角形中,其他两个角的度数不确定,故无法判定两三角形相似,故本选项错误,
故选:C.
6.解:∵△ABC∽△DEF,=2,
∴=4.
∵△ABC面积为8,
∴△DEF的面积==2.
故选:B.
7.解:∵AB∥CD∥EF,BD:DF=1:2,
∴AC:AE=1:3,故A选项正确;
CE:EA=2:3,故B选项错误;
CD:EF的值无法确定,故C选项错误;
AB:EF的值无法确定,故D选项错误;
故选:A.
8.解:A、所有的菱形,边长相等,所以对应边成比例,角不一定对应相等,所以不一定都相似,故本选项错误;
B、所有的正六边形,边长相等,所以对应边成比例,角都是120°,相等,所以都相似,故本选项正确;
C、所有的矩形,对应角的度数一定相同,但对应边的比值不一定相等,故本选项错误;
D、一个内角为80°的等腰三角形可能是顶角80°也可能是底角是80°,无法判断,此选项错误;
故选:B.
9.解:当CD是AB的垂线时,△ACD∽△CBD.
∵CD⊥AB,
∴∠CDA=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的角平分线,不符合题意;
B选项中,CD不与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不与AB垂直,不符合题意;
故选:C.
10.解:因为a、b、c、d是成比例线段,
可得:,
解得:d=4,
故选:B.
二.填空题
11.解:∵=,
∴a=b,
则==﹣.
故答案为:﹣.
12.解:∵=,
∴设a=2k,b=3k,
∴==﹣,
故答案为:﹣.
13.解:∵点P是线段AB的黄金分割点,且AP>PB,AB=10cm,
∴AP=AB≈6.18(cm).
故答案为6.18.
14.解:∵DE∥BC
∴,
∴=,
∴DE=,
故答案为:.
15.解:∵从图1到图2,图形形状没变,只是大小发生改变,
∴从图1到图2的变换是相似变换.
故答案为:相似,
16.解:∵两个相似三角形的周长的比等于1:4,
∴它们的相似比为1:4,
∴它们的面积的比等于1:16.
故答案为:1:16.
17.解:根据题意,5.8÷=5800000(厘米)=58(千米).
即实际距离是58千米.
故答案为:58.
18.解:设===a,
x=3a,y=4a,z=5a.
==,
故答案为:.
19.解:∵在Rt△ABC中,AC=1,BC=2,
∴AB=,AC:BC=1:2,
∴与Rt△ABC相似的格点三角形的两直角边的比值为1:2,
若该三角形最短边长为4,则另一直角边长为8,但在6×6网格图形中,最长线段为6,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出DE=,EF=2,DF=5的三角形,
∵===,
∴△ABC∽△DFE,
∴∠DEF=∠C=90°,
∴此时△DEF的面积为:×2÷2=10,△DEF为面积最大的三角形,其斜边长为:5.
故答案为:5.
20.解:∵四边形ABCD为正方形,
∴∠ADC=∠BCD=90°,AD=CD,
∵E和F分别为BC和CD中点,
∴DF=EC=2,
∴△ADF≌△DCE(SAS),
∴∠AFD=∠DEC,∠FAD=∠EDC,
∵∠EDC+∠DEC=90°,
∴∠EDC+∠AFD=90°,
∴∠DGF=90°,即DE⊥AF,故①正确;
∵AD=4,DF=CD=2,
∴AF=,
∴DG=AD×DF÷AF=,故②错误;
∵H为AF中点,
∴HD=HF=AF=,
∴∠HDF=∠HFD,
∵AB∥DC,
∴∠HDF=∠HFD=∠BAG,
∵AG==,AB=4,
∴,
∴△ABG~△DHF,故④正确;
∴∠ABG=∠DHF,而AB≠AG,
则∠ABG和∠AGB不相等,
故∠AGB≠∠DHF,
故HD与BG不平行,故③错误;
故答案为:①④.
三.解答题
21.解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
22.解:∵x:y=2:5,x:z=:=3:4,
∴x:y=6:15,x:z=6:8,
∴x:y:z=6:15:8.
23.解:∵AB=7,AC=1,
∴BD=AB﹣AC﹣CD=6﹣CD,
∵线段CD是线段AC和BD的比例中项,
∴CD2=AC?BD,
即CD2=1×(6﹣CD),
解得:CD=2.
24.解:==,得
a=c,b=c,
把a=c,b=c代入且a+b+c=36,得
c+c+c=36,
解得c=15,
a=c=9,
b=c=12,
△ABC三边的长:a=9,b=12,c=15.
25.解:(1)∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABD=36°,∠BDC=72°,
∴AD=BD,BC=BD,
∴△ABC∽△BDC,
∴=,即=,
∴AD2=AC?CD.
∴点D是线段AC的黄金分割点.
(2)∵点D是线段AC的黄金分割点,
∴AD=AC,
∵AC=2,
∴AD=﹣1.
26.解:(1)如图1,
由折叠过程可以看到:第一次折叠,A与D重合,四边形ABDC为正方形,折痕BC为对角线,由勾股定理可得BC=AB;第二次折叠,第一次的折痕与A4纸较长的边重合,即BC与较长边重合.所以,较长边=AB.
∴A4纸较长边与较短边的比为:.
故答案为:.
(2)A4纸与A5纸是相似图形.理由:
∵A4纸较长边与较短边的比为:,
∴设A4纸较短边的长为a,则较长边为a.
∵由图2可知:A5纸的长边与A4纸的短边重合,短边等于A4纸的长边的一半,
∴A5纸的长边为a,短边为.
∴A5纸的长边与短边的比为:=.
∴A4纸较长边与较短边的比=A5纸的长边与短边的比.
又∵A4纸与A5纸的四个角均为直角,
∴A4纸与A5纸相似.
27.解:①设AD=xcm,则BD=AB﹣AD=(12﹣x)cm
∵,
∴
解得x=7.2cm
∴AD=7.2cm;
②∵,
∴
即.
∴.
