2021-2022学年人教版八年级数学上册《12.1全等三角形》同步优生辅导训练(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册《12.1全等三角形》同步优生辅导训练(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 175.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 22:14:53 | ||
图片预览




文档简介
2021年人教版八年级数学上册《12.1全等三角形》同步优生辅导训练(附答案)
一.选择题(共11小题)
1.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中,与这100°角对应相等的角是( )
A.∠A B.∠B C.∠C D.∠B或∠C
2.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
3.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
4.如图,△ABE≌△ACF.若AB=5,AE=2,BE=4,则CF的长度是( )
A.2 B.5 C.4 D.3
5.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
A.50° B.60° C.100° D.120°
6.如图所示,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:
①BD是∠ABE的平分线;②AB⊥AC;③∠C=30°;④线段DE是△BDC的中线;⑤AD+BD=AC
其中正确的有( )个.
A.2 B.3 C.4 D.5
7.如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )
A.20° B.30° C.40° D.50°
8.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2.5 B.3 C.2.25或3 D.1或5
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150° B.180° C.210° D.225°
10.如图,已知△ABO≌△CDO,则下列结论不正确的是( )
A.AB=OD B.∠A=∠C C.AD=BC D.∠AOB=∠COD
11.如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
A.α=β B.α=2β C.α+β=90° D.α+2β=180°
二.填空题(共6小题)
12.如图,△ABC≌△AED,∠C=40°,∠EAC=30°,∠B=30°,则∠D= 度,∠EAD= 度.
13.如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB= .
14.如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若∠DEF=40°,PB=PF,则∠APF= °.
15.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为 .
16.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数为 .
17.如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= .
三.解答题(共4小题)
18.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
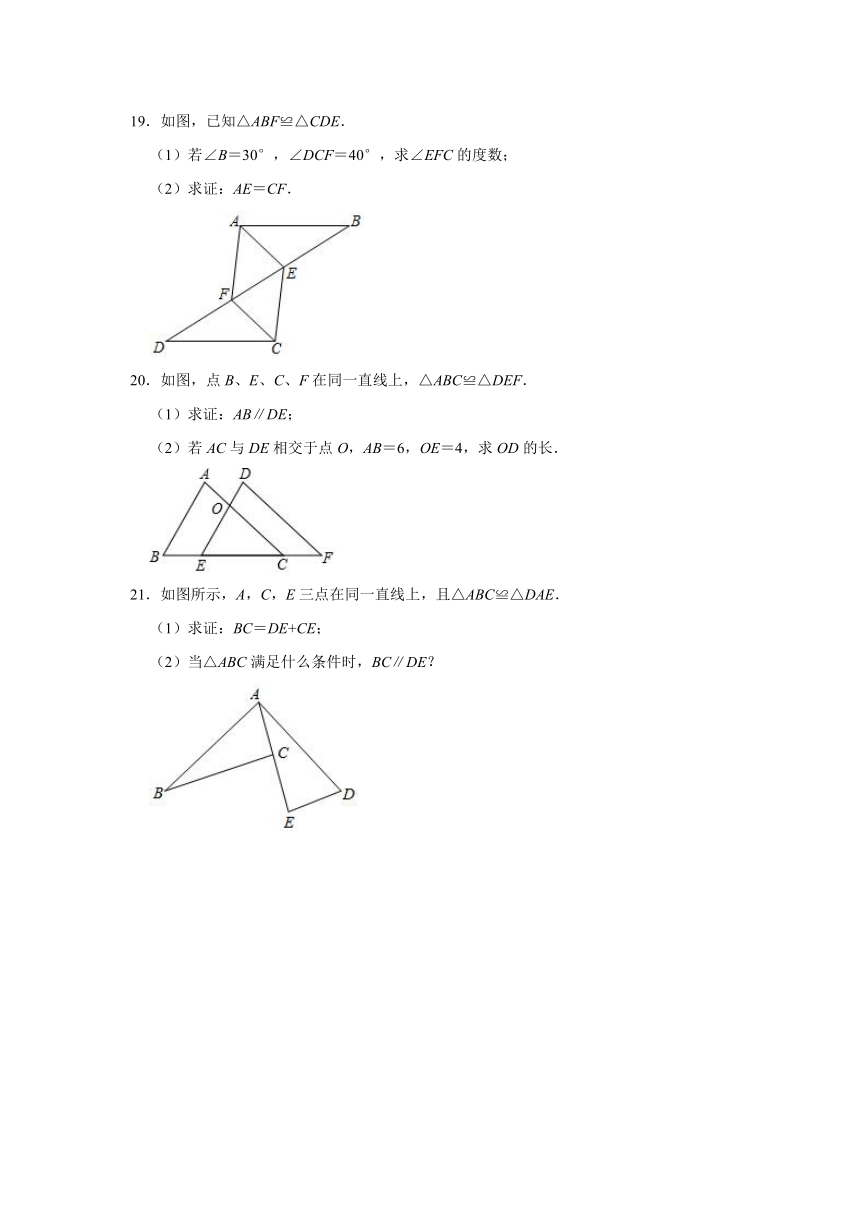
19.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)求证:AE=CF.
20.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
21.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
参考答案
一.选择题(共11小题)
1.解:在△ABC中,∵∠B=∠C,
∴∠B、∠C不能等于100°,
∴与△ABC全等的三角形的100°的角的对应角是∠A.
故选:A.
2.解:
∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,
∴∠DCE=∠B,
故选:A.
3.解:∵△ABC≌△AEF,
∴AC=AF,故①正确;
∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.
故选:C.
4.解:∵△ABE≌△ACF,
∴CF=BE=4,
故选:C.
5.解:∵△ABC≌△EDF,∠EDA=20°,∠F=60°,
∴∠B=∠EDF=20°,∠F=∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=100°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=50°,
故选:A.
6.解:①∵△ADB≌△EDB,
∴∠ABD=∠EBD,
∴BD是∠ABE的平分线,故①正确;
②∵△BDE≌△CDE,
∴BD=CD,BE=CE,
∴DE⊥BC,
∴∠BED=90°,
∵△ADB≌△EDB,
∴∠A=∠BED=90°,
∴AB⊥AD,
∵A、D、C可能不在同一直线上
∴AB可能不垂直于AC,故②不正确;
③∵△ADB≌△EDB,△BDE≌△CDE,
∴∠ABD=∠EBD,∠EBD=∠C,
∵∠A=90°
若A、D、C不在同一直线上,则∠ABD+∠EBD+∠C≠90°,
∴∠C≠30°,故③不正确;
④∵△BDE≌△CDE,
∴BE=CE,
∴线段DE是△BDC的中线,故④正确;
⑤∵△BDE≌△CDE,
∴BD=CD,
若A、D、C不在同一直线上,则AD+CD>AC,
∴AD+BD>AC,故⑤不正确.
故选:A.
7.解:∵△EDC≌△ABC,
∴∠DCE=∠ACB=100°,
∵A、C、D在同一条直线上,
∴∠ACD=180°,
∴∠BCE=∠ACB+∠DCE﹣∠ACD=20°,
故选:A.
8.解:∵△ABC中,AB=AC=12厘米,点D为AB的中点,
∴BD=6厘米,
若△BPD≌△CPQ,则需BD=CQ=6厘米,BP=CP=BC=×9=4.5(厘米),
∵点Q的运动速度为3厘米/秒,
∴点Q的运动时间为:6÷3=2(s),
∴v=4.5÷2=2.25(厘米/秒);
若△BPD≌△CQP,则需CP=BD=6厘米,BP=CQ,
∴,
解得:v=3;
∴v的值为:2.25或3,
故选:C.
9.解:由题意得:AB=ED,BC=DC,∠D=∠B=90°,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠1,
∠1+∠2=180°.
故选:B.
10.解:∵△ABO≌△CDO,
∴AO=OC,AB=CD,OB=OD,∠A=∠C,∠B=∠D,∠AOB=∠COD,
故选:A.
11.解:∵△AOB≌△ADC,
∴AB=AC,∠BAO=∠CAD,
∴∠BAC=∠OAD=α,
在△ABC中,∠ABC=(180°﹣α),
∵BC∥OA,
∴∠OBC=180°﹣∠O=180°﹣90°=90°,
∴β+(180°﹣α)=90°,
整理得,α=2β.故选:B.
二.填空题(共6小题)
12.解:△ABC中,∠C=40°,∠B=30°
∵△ABC≌△AED
∴∠D=∠C=40°,∠E=∠B=30°
∴∠EAD=180°﹣∠D﹣∠E=110°.
13.解:∵∠B=24°,∠CAB=54°,∠DAC=16°,
∴∠AFB=180°﹣(∠B+∠CAB+∠DAC)=86°,
∴∠GFD=∠AFB=86°,
∵△ABC≌△ADE,∠B=24°,
∴∠D=∠B=24°,
∴∠DGB=180°﹣∠D﹣∠DFG=70°,
故答案为:70°.
14.解:
∵△ABC≌△DEF,
∴∠B=∠DEF=40°,
∵PB=PF,
∴∠PFB=∠B=40°,
∴∠APF=∠B+∠PFB=80°,
故答案为:80.
15.解:∵在△ABC和△AED中
,
∴△ABC≌△AED(SAS),
∴∠1=∠AED,
∵∠AED+∠2=90°,
∴∠1+∠2=90°,故答案为:90°.
16.解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE,
又∠BAD=∠BAC﹣∠CAD,∠CAE=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵∠DAC=70°,∠BAE=100°,
∴∠BAD=(∠BAE﹣∠DAC)=(100°﹣70°)=15°,
在△ABG和△FDG中,
∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=15°.
故答案为:15°.
17.解:①当AP=CB时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=6;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=12,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,AP=6或12.
故答案为:6或12.
三.解答题(共4小题)
18.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
19.(1)解:∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠D+∠DCF=70°;
(2)证明:∵△ABF≌△CDE,
∴∠AFB=∠CED,AF=CE,
在△AFE和△CEF中,
,
∴△AFE≌△CEF(SAS),
∴AE=CF.
20.(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE;
(2)解:∵△ABC≌△DEF,
∴AB=DE=6,
∵OE=4,
∴OD=DE﹣OE=6﹣4=2.
21.(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
一.选择题(共11小题)
1.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中,与这100°角对应相等的角是( )
A.∠A B.∠B C.∠C D.∠B或∠C
2.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
3.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
4.如图,△ABE≌△ACF.若AB=5,AE=2,BE=4,则CF的长度是( )
A.2 B.5 C.4 D.3
5.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
A.50° B.60° C.100° D.120°
6.如图所示,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:
①BD是∠ABE的平分线;②AB⊥AC;③∠C=30°;④线段DE是△BDC的中线;⑤AD+BD=AC
其中正确的有( )个.
A.2 B.3 C.4 D.5
7.如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )
A.20° B.30° C.40° D.50°
8.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2.5 B.3 C.2.25或3 D.1或5
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150° B.180° C.210° D.225°
10.如图,已知△ABO≌△CDO,则下列结论不正确的是( )
A.AB=OD B.∠A=∠C C.AD=BC D.∠AOB=∠COD
11.如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
A.α=β B.α=2β C.α+β=90° D.α+2β=180°
二.填空题(共6小题)
12.如图,△ABC≌△AED,∠C=40°,∠EAC=30°,∠B=30°,则∠D= 度,∠EAD= 度.
13.如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB= .
14.如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若∠DEF=40°,PB=PF,则∠APF= °.
15.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为 .
16.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数为 .
17.如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= .
三.解答题(共4小题)
18.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
19.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)求证:AE=CF.
20.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
21.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
参考答案
一.选择题(共11小题)
1.解:在△ABC中,∵∠B=∠C,
∴∠B、∠C不能等于100°,
∴与△ABC全等的三角形的100°的角的对应角是∠A.
故选:A.
2.解:
∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,
∴∠DCE=∠B,
故选:A.
3.解:∵△ABC≌△AEF,
∴AC=AF,故①正确;
∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.
故选:C.
4.解:∵△ABE≌△ACF,
∴CF=BE=4,
故选:C.
5.解:∵△ABC≌△EDF,∠EDA=20°,∠F=60°,
∴∠B=∠EDF=20°,∠F=∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=100°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=50°,
故选:A.
6.解:①∵△ADB≌△EDB,
∴∠ABD=∠EBD,
∴BD是∠ABE的平分线,故①正确;
②∵△BDE≌△CDE,
∴BD=CD,BE=CE,
∴DE⊥BC,
∴∠BED=90°,
∵△ADB≌△EDB,
∴∠A=∠BED=90°,
∴AB⊥AD,
∵A、D、C可能不在同一直线上
∴AB可能不垂直于AC,故②不正确;
③∵△ADB≌△EDB,△BDE≌△CDE,
∴∠ABD=∠EBD,∠EBD=∠C,
∵∠A=90°
若A、D、C不在同一直线上,则∠ABD+∠EBD+∠C≠90°,
∴∠C≠30°,故③不正确;
④∵△BDE≌△CDE,
∴BE=CE,
∴线段DE是△BDC的中线,故④正确;
⑤∵△BDE≌△CDE,
∴BD=CD,
若A、D、C不在同一直线上,则AD+CD>AC,
∴AD+BD>AC,故⑤不正确.
故选:A.
7.解:∵△EDC≌△ABC,
∴∠DCE=∠ACB=100°,
∵A、C、D在同一条直线上,
∴∠ACD=180°,
∴∠BCE=∠ACB+∠DCE﹣∠ACD=20°,
故选:A.
8.解:∵△ABC中,AB=AC=12厘米,点D为AB的中点,
∴BD=6厘米,
若△BPD≌△CPQ,则需BD=CQ=6厘米,BP=CP=BC=×9=4.5(厘米),
∵点Q的运动速度为3厘米/秒,
∴点Q的运动时间为:6÷3=2(s),
∴v=4.5÷2=2.25(厘米/秒);
若△BPD≌△CQP,则需CP=BD=6厘米,BP=CQ,
∴,
解得:v=3;
∴v的值为:2.25或3,
故选:C.
9.解:由题意得:AB=ED,BC=DC,∠D=∠B=90°,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠1,
∠1+∠2=180°.
故选:B.
10.解:∵△ABO≌△CDO,
∴AO=OC,AB=CD,OB=OD,∠A=∠C,∠B=∠D,∠AOB=∠COD,
故选:A.
11.解:∵△AOB≌△ADC,
∴AB=AC,∠BAO=∠CAD,
∴∠BAC=∠OAD=α,
在△ABC中,∠ABC=(180°﹣α),
∵BC∥OA,
∴∠OBC=180°﹣∠O=180°﹣90°=90°,
∴β+(180°﹣α)=90°,
整理得,α=2β.故选:B.
二.填空题(共6小题)
12.解:△ABC中,∠C=40°,∠B=30°
∵△ABC≌△AED
∴∠D=∠C=40°,∠E=∠B=30°
∴∠EAD=180°﹣∠D﹣∠E=110°.
13.解:∵∠B=24°,∠CAB=54°,∠DAC=16°,
∴∠AFB=180°﹣(∠B+∠CAB+∠DAC)=86°,
∴∠GFD=∠AFB=86°,
∵△ABC≌△ADE,∠B=24°,
∴∠D=∠B=24°,
∴∠DGB=180°﹣∠D﹣∠DFG=70°,
故答案为:70°.
14.解:
∵△ABC≌△DEF,
∴∠B=∠DEF=40°,
∵PB=PF,
∴∠PFB=∠B=40°,
∴∠APF=∠B+∠PFB=80°,
故答案为:80.
15.解:∵在△ABC和△AED中
,
∴△ABC≌△AED(SAS),
∴∠1=∠AED,
∵∠AED+∠2=90°,
∴∠1+∠2=90°,故答案为:90°.
16.解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE,
又∠BAD=∠BAC﹣∠CAD,∠CAE=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵∠DAC=70°,∠BAE=100°,
∴∠BAD=(∠BAE﹣∠DAC)=(100°﹣70°)=15°,
在△ABG和△FDG中,
∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=15°.
故答案为:15°.
17.解:①当AP=CB时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=6;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=12,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,AP=6或12.
故答案为:6或12.
三.解答题(共4小题)
18.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
19.(1)解:∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠D+∠DCF=70°;
(2)证明:∵△ABF≌△CDE,
∴∠AFB=∠CED,AF=CE,
在△AFE和△CEF中,
,
∴△AFE≌△CEF(SAS),
∴AE=CF.
20.(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE;
(2)解:∵△ABC≌△DEF,
∴AB=DE=6,
∵OE=4,
∴OD=DE﹣OE=6﹣4=2.
21.(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
