2021-2022学年人教版八年级数学上册《12.2全等三角形的判定》同步优生辅导训练(word版答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册《12.2全等三角形的判定》同步优生辅导训练(word版答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 250.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 00:00:00 | ||
图片预览

文档简介
2021年人教版八年级数学上册《12.2全等三角形的判定》同步优生辅导训练(附答案)
一.选择题(共5小题)
1.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF B.∠A=∠D C.AC=DF D.AC∥DF
2.如图已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
3.如图,在△ABC中,∠B=40°,AB=CB,AF=CD,AE=CF,则∠EFD=( )
A.50° B.60° C.70° D.80°
4.如图,AB=AC,点D、E分别是AB、AC上一点,AD=AE,BE、CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50° B.65° C.70° D.80°
5.如图,E是线段AB的中点,∠AEC=∠DEB,再添加一个条件,使得△AED≌△BEC,所添加的条件不正确的是( )
A.AD=BC B.DE=CE C.∠A=∠B D.∠C=∠D
二.填空题(共7小题)
6.如图,点E、F在BC上,AB=DC,∠B=∠C,请补充一个条件: ,使△ABF≌△DCE.
7.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
8.如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=∠B=40°,DE交线段AC于点E.下列结论:①∠CDE=∠BAD;②BD=CE;③当D为BC中点时,DE⊥AC;④当△ADE为等腰三角形时,∠BAD=30°.其中正确的是 (填序号).
9.如图所示,A、B在一水池的两侧,若BE=DE,∠B=∠D=90°,CD=8m,则水池宽AB= m.
10.如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB= .
11.如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB= .
12.如图,△ABC中,∠ACB=90°,点D在边AC上,DE⊥AB于点E,DC=DE,∠A=32°,则∠BDC的度数为 .
三.解答题(共9小题)
13.如图,E为BC上一点,AC∥BD,AC=BE,∠ABC=∠D.求证:AB=ED.
14.如图,△ABC和△DEF中,AB=DE,AC=DF,BE=CF;
(1)试说明△ABC≌△DEF.
(2)若∠ABC=38°,求∠DEF.
15.如图,在△ABC中,AC=BC,点D在AB边上,点E在BC边上,连接CD,DE.已知∠ACD=∠BDE,CD=DE.
(1)猜想AC与BD的数量关系,并证明你的猜想;
(2)若AD=3,BD=5,求CE的长.
16.如图,点E在△ABC的边AC上,且∠ABE=∠C,AF平分∠BAE交BE于F,FD∥BC交AC于点D.
(1)求证:△ABF≌△ADF;
(2)若BE=7,AB=8,AE=5,求△EFD的周长.
17.如图,已知AD、BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN;
(2)试猜想OA与OD的大小关系,并说明理由.
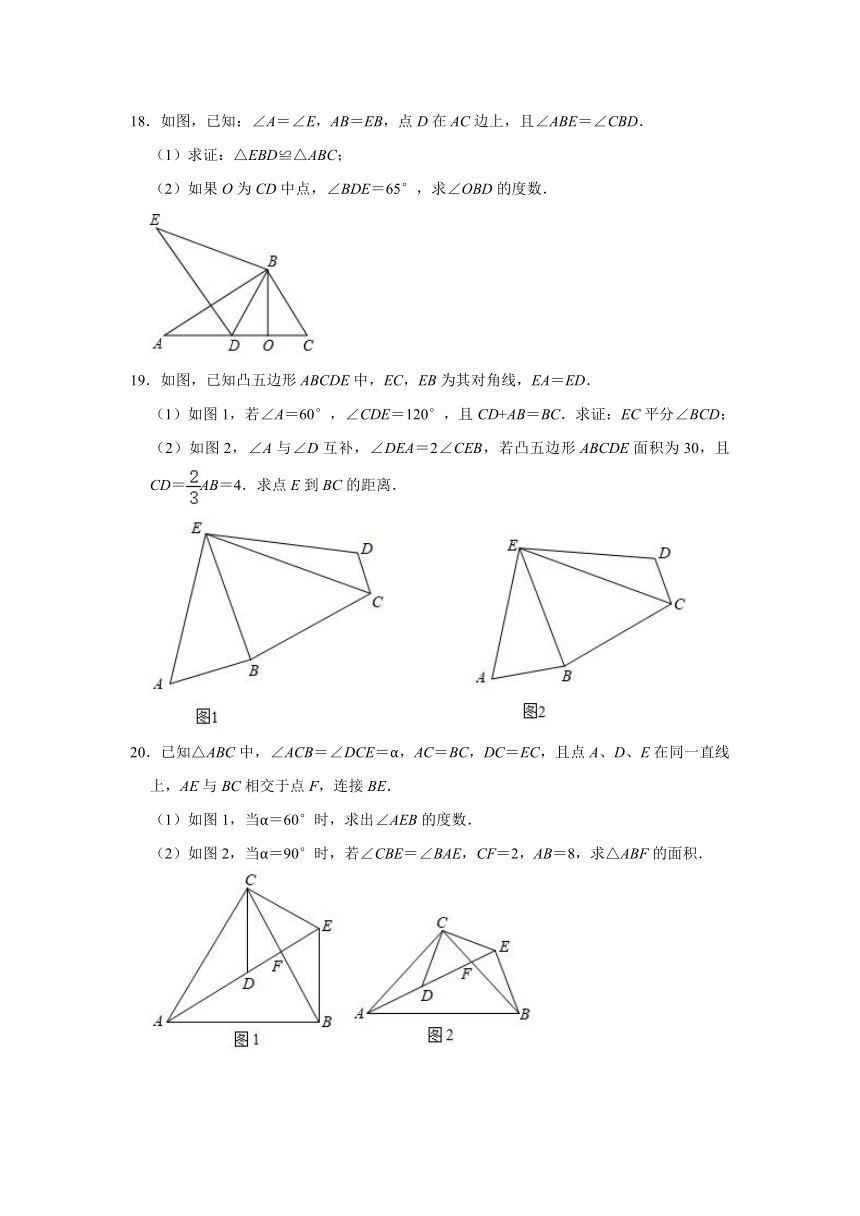
18.如图,已知:∠A=∠E,AB=EB,点D在AC边上,且∠ABE=∠CBD.
(1)求证:△EBD≌△ABC;
(2)如果O为CD中点,∠BDE=65°,求∠OBD的度数.
19.如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED.
(1)如图1,若∠A=60°,∠CDE=120°,且CD+AB=BC.求证:EC平分∠BCD;
(2)如图2,∠A与∠D互补,∠DEA=2∠CEB,若凸五边形ABCDE面积为30,且CD=AB=4.求点E到BC的距离.
20.已知△ABC中,∠ACB=∠DCE=α,AC=BC,DC=EC,且点A、D、E在同一直线上,AE与BC相交于点F,连接BE.
(1)如图1,当α=60°时,求出∠AEB的度数.
(2)如图2,当α=90°时,若∠CBE=∠BAE,CF=2,AB=8,求△ABF的面积.
21.如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.试说明:
(1)△ABP≌△AEQ;
(2)EF=BF.
参考答案
一.选择题(共5小题)
1.解:A、BE=CF可以求出BC=EF,然后利用“SAS”证明△ABC≌△DEF,故本选项错误;
B、∠A=∠D可以利用“ASA”证明△ABC≌△DEF,故本选项错误;
C、AC=DF符合“SSA”,不能证明△ABC≌△DEF,故本选项正确.
D、由AC∥DF可得∠F=∠ACB,然后利用“AAS”证明△ABC≌△DEF,故本选项错误.
故选:C.
2.解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选:B.
3.解:∵∠B=40°,AB=CB,
∴∠A=∠C=(180°﹣40°)=70°,
在△AEF和△CFD中,
,
∴△AEF≌△CFD(SAS),
∴∠AFE=∠CDF,
∵∠AFE+∠EFD+∠CFD=180°,∠C+∠CDF+∠CFD=180°,
∴∠EFD=∠C=70°.
故选:C.
4.解:在△ADC与△AEB中,
,
∴△ADC≌△AEB(SAS),
∴∠B=∠C,∠AEB=∠ADC,
∵∠BAC=70°,∠C=30°,
∴∠AEB=∠ADC=180°﹣∠BAC﹣∠C=180°﹣70°﹣30°=80°,
∴∠BMC=∠DME=360°﹣∠AEB﹣∠ADC﹣∠BAC=360°﹣80°﹣80°﹣70°=130°,
∴∠BMD=180°﹣130°=50°,
故选:A.
5.解:∵∠AEC=∠DEB,
∴∠AED=∠BEC,
∵E是线段AB的中点,
∴AE=BE,
A、添加AD=BC,不能判定△AED≌△BEC,符合题意;
B、添加DE=CE,利用SAS能判定△AED≌△BEC,不符合题意;
C、添加∠A=∠B,利用ASA能判定△AED≌△BEC,不符合题意;
D、添加∠C=∠D,利用AAS能判定△AED≌△BEC,不符合题意;
故选:A.
二.填空题(共7小题)
6.解:根据SAS判断△ABF≌△DCE,可以添加BE=CF或BF=EC.
根据AAS判断△ABF≌△DCE,可以添加∠AFB=∠DEC.
根据ASA判断△ABF≌△DCE,可以添加∠A=∠D.
故答案为BE=CF或BF=EC或∠A=∠D或∠AFB=∠DEC.
7.解:在△ACE和△ADE中,
,
∴△ACE≌△ADE(SSS),
∴∠CAE=∠DAE,
在△CAB和△DAB中,
∴△CAB≌△DAB(SAS),
∴BC=BD,
在△BCE和△BDE中,
∴△BCE≌△BDE(SSS).
∴图中全等三角形有3对.
故答案为:3.
8.解:①∵∠ADC=∠B+∠BAD,∠B=∠ADE=40°,
∴∠BAD=∠CDE;故①正确;
②∵AB=AC,
∴∠B=∠C=40°,
由①知:∠BAD=∠CDE
当△ABD≌△DCE时,BD=CE,
故②不正确;
③∵D为BC中点,AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴∠CDE=50°,
∵∠C=40°,
∴∠DEC=90°,
∴DE⊥AC,故③正确;
④∵∠C=40°,
∴∠AED>40°,
∴∠ADE≠∠AED,
∵△ADE为等腰三角形,
∴AE=DE或AD=DE,
当AE=DE时,∠DAE=∠ADE=40°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=60°,故④不正确,
故答案为:①③.
9.解:∵∠B=∠D,BE=DE,∠AEB=∠CED,
∴△ABE≌△CDE,
∴AB=CD=8m.
故填8.
10.解:在△ACO和△BCO中,
,
∴△AOC≌△BOC(SSS),
∴∠BCO=∠ACO=30°,
∴∠ACB=∠BCO+∠ACO=60°,
故答案为60°.
11.解:在Rt△ADE和Rt△ADC中,
,
∴Rt△ADE≌Rt△ADC(HL),
∴AC=AE=3,
∴BE=AB﹣AE=2,
故答案为2.
12.解:在Rt△BCD和Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴∠CDB=∠EDB,
∵∠CDE=∠A+∠AED=32°+90°=122°,
∴∠CDB=∠EDB=61°,
故答案为:61°.
三.解答题(共9小题)
13.解:∵AC∥BE,
∴∠C=∠EBD,
在△ABC与△EDB中,
,
∴△ABC≌△EDB(AAS),
∴AB=ED.
14.解:(1)∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)由(1)知:△ABC≌△DEF,
∴∠DEF=∠ABC,
∵∠ABC=38°,
∴∠DEF=38°.
15.解:(1)AC=BD,理由如下:
∵AC=BC,
∴∠A=∠B,
在△ADC和△BED中,
,
∴△ADC≌△BED(AAS),
∴AC=BD;
(2)由(1)知:△ADC≌△BED,
∴AC=BD=5,BE=AD=3,
∴BC=AC=5,
∴CE=BC﹣BE=2.
16.解:(1)∵FD∥BC,
∴∠ADF=∠C,
∵∠ABF=∠C,
∴∠ABF=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠CAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS);
(2)∵△ABF≌△ADF,
∴AD=AB=8,BF=DF,
∵AE=5,
∴DE=AD=AE=8﹣5=3,
∴△EFD的周长=EF+DF+DE=EF+BF+DE=BE+DE=7+3=10.
17.(1)证明:∵BN=CM,
∴BN+MN=MN+CM,
即CN=BM,
∵AM⊥BC于点M,DN⊥BC于点N,
∴∠AMB=∠DNC=90°,
在Rt△ABM和Rt△DCN中,
,
∴Rt△ABM≌Rt△DCN(HL);
(2)解:OA=OD,理由如下:
∵Rt△ABM≌Rt△DCN,
∴AM=DN,
在△AMO和△DNO中,
,
∴△AMO≌△DNO(AAS),
∴OA=OD.
18.(1)证明:∵∠ABE=∠CBD,
∴∠ABE+∠ABD=∠CBD+∠ABD,
即∠EBD=∠ABC.
在△EBD和△ABC中,
,
∴△EBD≌△ABC(ASA);
(2)解:∵△EBD≌△ABD,
∴BD=BC,∠BDE=∠C,
∵∠BDE=65°,
∴∠BDC=∠BDE=65°,
∵∠CBD=50°,
∵O点为CD中点,
∴∠OBD=CBD=25°.
19.(1)证明:延长CD到T,使得DT=BA,连接ET.
∵∠CDE=120°,
∴∠EDT=180°﹣120°=60°,
∵∠A=60°,
∴∠A=∠EDT,
在△EAB和△EDT中,
,
∴△EAB≌△EDT(SAS),
∴EB=ET,
∴CB=CD+BA=CD+DT=CT,
在△ECB和△ECT中,
,
∴△ECB≌△ECT(SSS),
∴∠ECB=∠ECD.
(2)解:延长CD到Q,使得∠QED=∠AEB,过点E作EH⊥BC于H.
∵∠A+∠CDE=180°,∠CDE+∠EDQ=180°,
∴∠A=∠EDQ,
在△AEB和△DEQ中,
,
∴△AEB≌△DEQ(ASA),
∴EB=EQ,
∵∠AED=2∠BEC,
∴∠AEB+∠CED=∠BEC,
∴∠CED+∠DEQ=∠BEC,
∴∠CEB=∠CEQ,
在△CEB和△CEQ中,
,
∴△EC≌△ECQ(SAS),
∵S五边形ABCDE=S四边形EBCQ=2S△EBC=30°,
∴S△EBC=15,
∵CD=AB=4,
∴AB=6,CD=4,
∴BC=CD+QD=CD+AB=10,
∴×10×EH=15,
∴EH=3,
∴点E到BC的距离为3.
20.解:(1)∵∠ACB=∠DCE=60°,CA=CB,CD=CE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∵∠CFA=∠BFE,
∴∠AEB=∠ACF=60°.
(2)同理可证△ACD≌△BCE,
∴∠CAF=∠CBE,
∵∠CBE=∠BAE,
∴∠CAF=∠BAE,
∴AF平分∠CAB,
∵FC⊥AC,CF=2,
∴点F到AB的距离=CF=2,
∴S△ABF=?AB?CF=×8×2=8.
21.解:(1)∵△ABE和△APQ是等边三角形,
∴AB=AE,AP=AQ,∠BAE=∠PAQ=∠ABE=∠AEB=60°,
∴∠BAE﹣∠PAE=∠PAQ﹣∠PAE,
∴∠BAP=∠EAQ.
在△ABP和△AEQ中,
,
∴△QAE≌△PAB(SAS);
(2)∵△QAE≌△PAB
∴∠ABP=∠AEQ=90°.
∴∠AEF=90°,
∴∠ABP=∠AEF
∴∠ABP﹣∠AEB=∠AEF﹣∠ABE,
∴∠BEF=∠EBF,
∴BF=EF.
一.选择题(共5小题)
1.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF B.∠A=∠D C.AC=DF D.AC∥DF
2.如图已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
3.如图,在△ABC中,∠B=40°,AB=CB,AF=CD,AE=CF,则∠EFD=( )
A.50° B.60° C.70° D.80°
4.如图,AB=AC,点D、E分别是AB、AC上一点,AD=AE,BE、CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50° B.65° C.70° D.80°
5.如图,E是线段AB的中点,∠AEC=∠DEB,再添加一个条件,使得△AED≌△BEC,所添加的条件不正确的是( )
A.AD=BC B.DE=CE C.∠A=∠B D.∠C=∠D
二.填空题(共7小题)
6.如图,点E、F在BC上,AB=DC,∠B=∠C,请补充一个条件: ,使△ABF≌△DCE.
7.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
8.如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=∠B=40°,DE交线段AC于点E.下列结论:①∠CDE=∠BAD;②BD=CE;③当D为BC中点时,DE⊥AC;④当△ADE为等腰三角形时,∠BAD=30°.其中正确的是 (填序号).
9.如图所示,A、B在一水池的两侧,若BE=DE,∠B=∠D=90°,CD=8m,则水池宽AB= m.
10.如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB= .
11.如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB= .
12.如图,△ABC中,∠ACB=90°,点D在边AC上,DE⊥AB于点E,DC=DE,∠A=32°,则∠BDC的度数为 .
三.解答题(共9小题)
13.如图,E为BC上一点,AC∥BD,AC=BE,∠ABC=∠D.求证:AB=ED.
14.如图,△ABC和△DEF中,AB=DE,AC=DF,BE=CF;
(1)试说明△ABC≌△DEF.
(2)若∠ABC=38°,求∠DEF.
15.如图,在△ABC中,AC=BC,点D在AB边上,点E在BC边上,连接CD,DE.已知∠ACD=∠BDE,CD=DE.
(1)猜想AC与BD的数量关系,并证明你的猜想;
(2)若AD=3,BD=5,求CE的长.
16.如图,点E在△ABC的边AC上,且∠ABE=∠C,AF平分∠BAE交BE于F,FD∥BC交AC于点D.
(1)求证:△ABF≌△ADF;
(2)若BE=7,AB=8,AE=5,求△EFD的周长.
17.如图,已知AD、BC相交于点O,AB=CD,AM⊥BC于点M,DN⊥BC于点N,BN=CM.
(1)求证:△ABM≌△DCN;
(2)试猜想OA与OD的大小关系,并说明理由.
18.如图,已知:∠A=∠E,AB=EB,点D在AC边上,且∠ABE=∠CBD.
(1)求证:△EBD≌△ABC;
(2)如果O为CD中点,∠BDE=65°,求∠OBD的度数.
19.如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED.
(1)如图1,若∠A=60°,∠CDE=120°,且CD+AB=BC.求证:EC平分∠BCD;
(2)如图2,∠A与∠D互补,∠DEA=2∠CEB,若凸五边形ABCDE面积为30,且CD=AB=4.求点E到BC的距离.
20.已知△ABC中,∠ACB=∠DCE=α,AC=BC,DC=EC,且点A、D、E在同一直线上,AE与BC相交于点F,连接BE.
(1)如图1,当α=60°时,求出∠AEB的度数.
(2)如图2,当α=90°时,若∠CBE=∠BAE,CF=2,AB=8,求△ABF的面积.
21.如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.试说明:
(1)△ABP≌△AEQ;
(2)EF=BF.
参考答案
一.选择题(共5小题)
1.解:A、BE=CF可以求出BC=EF,然后利用“SAS”证明△ABC≌△DEF,故本选项错误;
B、∠A=∠D可以利用“ASA”证明△ABC≌△DEF,故本选项错误;
C、AC=DF符合“SSA”,不能证明△ABC≌△DEF,故本选项正确.
D、由AC∥DF可得∠F=∠ACB,然后利用“AAS”证明△ABC≌△DEF,故本选项错误.
故选:C.
2.解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选:B.
3.解:∵∠B=40°,AB=CB,
∴∠A=∠C=(180°﹣40°)=70°,
在△AEF和△CFD中,
,
∴△AEF≌△CFD(SAS),
∴∠AFE=∠CDF,
∵∠AFE+∠EFD+∠CFD=180°,∠C+∠CDF+∠CFD=180°,
∴∠EFD=∠C=70°.
故选:C.
4.解:在△ADC与△AEB中,
,
∴△ADC≌△AEB(SAS),
∴∠B=∠C,∠AEB=∠ADC,
∵∠BAC=70°,∠C=30°,
∴∠AEB=∠ADC=180°﹣∠BAC﹣∠C=180°﹣70°﹣30°=80°,
∴∠BMC=∠DME=360°﹣∠AEB﹣∠ADC﹣∠BAC=360°﹣80°﹣80°﹣70°=130°,
∴∠BMD=180°﹣130°=50°,
故选:A.
5.解:∵∠AEC=∠DEB,
∴∠AED=∠BEC,
∵E是线段AB的中点,
∴AE=BE,
A、添加AD=BC,不能判定△AED≌△BEC,符合题意;
B、添加DE=CE,利用SAS能判定△AED≌△BEC,不符合题意;
C、添加∠A=∠B,利用ASA能判定△AED≌△BEC,不符合题意;
D、添加∠C=∠D,利用AAS能判定△AED≌△BEC,不符合题意;
故选:A.
二.填空题(共7小题)
6.解:根据SAS判断△ABF≌△DCE,可以添加BE=CF或BF=EC.
根据AAS判断△ABF≌△DCE,可以添加∠AFB=∠DEC.
根据ASA判断△ABF≌△DCE,可以添加∠A=∠D.
故答案为BE=CF或BF=EC或∠A=∠D或∠AFB=∠DEC.
7.解:在△ACE和△ADE中,
,
∴△ACE≌△ADE(SSS),
∴∠CAE=∠DAE,
在△CAB和△DAB中,
∴△CAB≌△DAB(SAS),
∴BC=BD,
在△BCE和△BDE中,
∴△BCE≌△BDE(SSS).
∴图中全等三角形有3对.
故答案为:3.
8.解:①∵∠ADC=∠B+∠BAD,∠B=∠ADE=40°,
∴∠BAD=∠CDE;故①正确;
②∵AB=AC,
∴∠B=∠C=40°,
由①知:∠BAD=∠CDE
当△ABD≌△DCE时,BD=CE,
故②不正确;
③∵D为BC中点,AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴∠CDE=50°,
∵∠C=40°,
∴∠DEC=90°,
∴DE⊥AC,故③正确;
④∵∠C=40°,
∴∠AED>40°,
∴∠ADE≠∠AED,
∵△ADE为等腰三角形,
∴AE=DE或AD=DE,
当AE=DE时,∠DAE=∠ADE=40°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=60°,故④不正确,
故答案为:①③.
9.解:∵∠B=∠D,BE=DE,∠AEB=∠CED,
∴△ABE≌△CDE,
∴AB=CD=8m.
故填8.
10.解:在△ACO和△BCO中,
,
∴△AOC≌△BOC(SSS),
∴∠BCO=∠ACO=30°,
∴∠ACB=∠BCO+∠ACO=60°,
故答案为60°.
11.解:在Rt△ADE和Rt△ADC中,
,
∴Rt△ADE≌Rt△ADC(HL),
∴AC=AE=3,
∴BE=AB﹣AE=2,
故答案为2.
12.解:在Rt△BCD和Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴∠CDB=∠EDB,
∵∠CDE=∠A+∠AED=32°+90°=122°,
∴∠CDB=∠EDB=61°,
故答案为:61°.
三.解答题(共9小题)
13.解:∵AC∥BE,
∴∠C=∠EBD,
在△ABC与△EDB中,
,
∴△ABC≌△EDB(AAS),
∴AB=ED.
14.解:(1)∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)由(1)知:△ABC≌△DEF,
∴∠DEF=∠ABC,
∵∠ABC=38°,
∴∠DEF=38°.
15.解:(1)AC=BD,理由如下:
∵AC=BC,
∴∠A=∠B,
在△ADC和△BED中,
,
∴△ADC≌△BED(AAS),
∴AC=BD;
(2)由(1)知:△ADC≌△BED,
∴AC=BD=5,BE=AD=3,
∴BC=AC=5,
∴CE=BC﹣BE=2.
16.解:(1)∵FD∥BC,
∴∠ADF=∠C,
∵∠ABF=∠C,
∴∠ABF=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠CAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS);
(2)∵△ABF≌△ADF,
∴AD=AB=8,BF=DF,
∵AE=5,
∴DE=AD=AE=8﹣5=3,
∴△EFD的周长=EF+DF+DE=EF+BF+DE=BE+DE=7+3=10.
17.(1)证明:∵BN=CM,
∴BN+MN=MN+CM,
即CN=BM,
∵AM⊥BC于点M,DN⊥BC于点N,
∴∠AMB=∠DNC=90°,
在Rt△ABM和Rt△DCN中,
,
∴Rt△ABM≌Rt△DCN(HL);
(2)解:OA=OD,理由如下:
∵Rt△ABM≌Rt△DCN,
∴AM=DN,
在△AMO和△DNO中,
,
∴△AMO≌△DNO(AAS),
∴OA=OD.
18.(1)证明:∵∠ABE=∠CBD,
∴∠ABE+∠ABD=∠CBD+∠ABD,
即∠EBD=∠ABC.
在△EBD和△ABC中,
,
∴△EBD≌△ABC(ASA);
(2)解:∵△EBD≌△ABD,
∴BD=BC,∠BDE=∠C,
∵∠BDE=65°,
∴∠BDC=∠BDE=65°,
∵∠CBD=50°,
∵O点为CD中点,
∴∠OBD=CBD=25°.
19.(1)证明:延长CD到T,使得DT=BA,连接ET.
∵∠CDE=120°,
∴∠EDT=180°﹣120°=60°,
∵∠A=60°,
∴∠A=∠EDT,
在△EAB和△EDT中,
,
∴△EAB≌△EDT(SAS),
∴EB=ET,
∴CB=CD+BA=CD+DT=CT,
在△ECB和△ECT中,
,
∴△ECB≌△ECT(SSS),
∴∠ECB=∠ECD.
(2)解:延长CD到Q,使得∠QED=∠AEB,过点E作EH⊥BC于H.
∵∠A+∠CDE=180°,∠CDE+∠EDQ=180°,
∴∠A=∠EDQ,
在△AEB和△DEQ中,
,
∴△AEB≌△DEQ(ASA),
∴EB=EQ,
∵∠AED=2∠BEC,
∴∠AEB+∠CED=∠BEC,
∴∠CED+∠DEQ=∠BEC,
∴∠CEB=∠CEQ,
在△CEB和△CEQ中,
,
∴△EC≌△ECQ(SAS),
∵S五边形ABCDE=S四边形EBCQ=2S△EBC=30°,
∴S△EBC=15,
∵CD=AB=4,
∴AB=6,CD=4,
∴BC=CD+QD=CD+AB=10,
∴×10×EH=15,
∴EH=3,
∴点E到BC的距离为3.
20.解:(1)∵∠ACB=∠DCE=60°,CA=CB,CD=CE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∵∠CFA=∠BFE,
∴∠AEB=∠ACF=60°.
(2)同理可证△ACD≌△BCE,
∴∠CAF=∠CBE,
∵∠CBE=∠BAE,
∴∠CAF=∠BAE,
∴AF平分∠CAB,
∵FC⊥AC,CF=2,
∴点F到AB的距离=CF=2,
∴S△ABF=?AB?CF=×8×2=8.
21.解:(1)∵△ABE和△APQ是等边三角形,
∴AB=AE,AP=AQ,∠BAE=∠PAQ=∠ABE=∠AEB=60°,
∴∠BAE﹣∠PAE=∠PAQ﹣∠PAE,
∴∠BAP=∠EAQ.
在△ABP和△AEQ中,
,
∴△QAE≌△PAB(SAS);
(2)∵△QAE≌△PAB
∴∠ABP=∠AEQ=90°.
∴∠AEF=90°,
∴∠ABP=∠AEF
∴∠ABP﹣∠AEB=∠AEF﹣∠ABE,
∴∠BEF=∠EBF,
∴BF=EF.
