2021-2022学年人教五四新版六年级上册数学《第3章 圆的初步认识》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年人教五四新版六年级上册数学《第3章 圆的初步认识》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 19:26:03 | ||
图片预览



文档简介
2021-2022学年人教五四新版六年级上册数学《第3章
圆的初步认识》单元测试卷
一.选择题
1.过圆上一点可以作出圆的最长弦的条数为( )
A.1条
B.2条
C.3条
D.无数条
2.下列说法正确的是( )
A.长度相等的两条弧是等弧
B.优弧一定大于劣弧
C.不同的圆中不可能有相等的弦
D.直径是弦且同一个圆中最长的弦
3.等于圆周的弧叫做( )
A.劣弧
B.半圆
C.优弧
D.圆
4.下列说法中,不正确的是( )
A.直径是弦,弦是直径
B.半圆周是弧
C.圆上的点到圆心的距离都相等
D.同圆或等圆中,优弧一定比劣弧长
5.已知扇形的半径为6,圆心角为60°,则这个扇形的面积为( )
A.9π
B.6π
C.3π
D.π
6.如图,⊙O的半径为1,分别以⊙O的直径AB上的两个四等分点O1,O2为圆心,为半径作圆,则图中阴影部分的面积为( )
A.π
B.π
C.π
D.2π
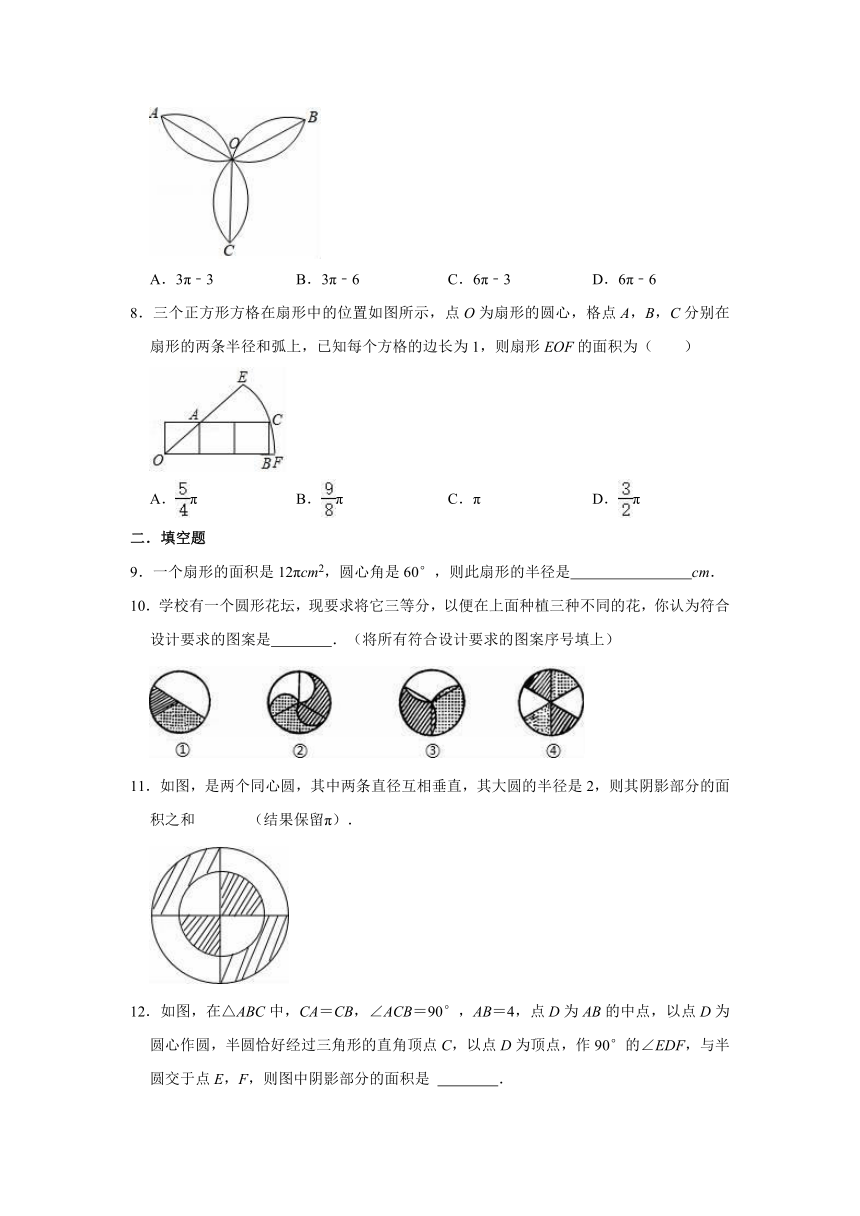
7.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA=OB=OC=2,则这朵三叶花的面积为( )
A.3π﹣3
B.3π﹣6
C.6π﹣3
D.6π﹣6
8.三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形EOF的面积为( )
A.π
B.π
C.π
D.π
二.填空题
9.一个扇形的面积是12πcm2,圆心角是60°,则此扇形的半径是
cm.
10.学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花,你认为符合设计要求的图案是
.(将所有符合设计要求的图案序号填上)
11.如图,是两个同心圆,其中两条直径互相垂直,其大圆的半径是2,则其阴影部分的面积之和
(结果保留π).
12.如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是
.
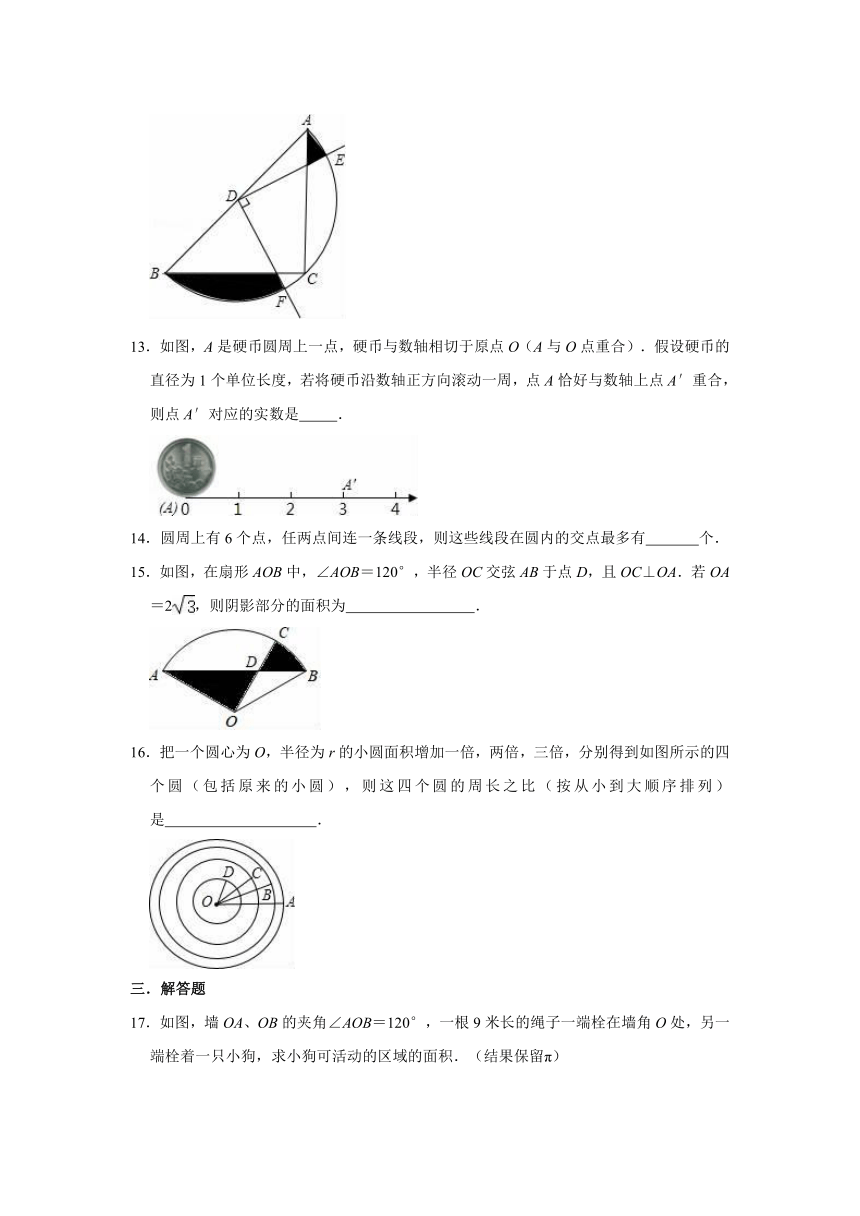
13.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是
.
14.圆周上有6个点,任两点间连一条线段,则这些线段在圆内的交点最多有
个.
15.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为
.
16.把一个圆心为O,半径为r的小圆面积增加一倍,两倍,三倍,分别得到如图所示的四个圆(包括原来的小圆),则这四个圆的周长之比(按从小到大顺序排列)是
.
三.解答题
17.如图,墙OA、OB的夹角∠AOB=120°,一根9米长的绳子一端栓在墙角O处,另一端栓着一只小狗,求小狗可活动的区域的面积.(结果保留π)
18.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
19.如图扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,求贴纸部分的面积.
20.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
21.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
参考答案与试题解析
一.选择题
1.解:圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选:A.
2.解:A、等弧指的是在同圆或等圆中,能够互相重合的弧,而不是长度相等,就一定能够重合,故错误;
B、不在同圆或等圆中,故错误;
C、等弦即只要长度相等即可,故错误;
D、正确.
故选:D.
3.解:根据直径所对的两条弧是半圆,大于半圆的弧是优弧,则等于圆周的弧叫做优弧.
故选:C.
4.解:A、直径是圆内最长的弦,但弦不一定是直径,故本选项错误;
B、半圆周是圆弧,故本选项正确;
C、圆上的点到圆心的距离都等于半径,故本选项正确;
D、同圆中,优弧是大于半圆的弧,而劣弧是小于半圆的弧,故本选项正确.
故选:A.
5.解:∵扇形的半径为6cm,圆心角为60°,
∴S==6π.
故选:B.
6.解:π×12×
=π×1×
=π.
答:图中阴影部分的面积为π.
故选:B.
7.解:如图所示:弧OA是⊙M上满足条件的一段弧,连接AM、MO,
由题意知:∠AMO=90°,AM=OM
∵AO=2,∴AM=.
∵S扇形AMO=×π×MA2=.
S△AMO=AM?MO=1,
∴S弓形AO=﹣1,
∴S三叶花=6×(﹣1)
=3π﹣6.
故选:B.
8.解:连接OC,
由勾股定理得:OC==,
由正方形的性质得:∠EOB=45°,
所以扇形EOF的面积为:=π,
故选:A.
二.填空题
9.解:设这个扇形的半径是rcm.
根据扇形面积公式,得=12π,
解得r=±6(负值舍去).
故答案为6.
10.解:②③④符合要求.
11.解:由题意得,阴影部分的面积之和正好是半圆,则阴影部分的面积之和2π.
12.解:连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=AB=2,四边形DMCN是正方形,DM=.
则扇形FDE的面积是:=π.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
在△DMG和△DNH中,
,
∴△DMG≌△DNH(AAS),
∴S四边形DGCH=S四边形DMCN=2.
则阴影部分的面积是:π﹣2.
故答案为:π﹣2.
13.解:将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A'重合,则转过的距离是圆的周长是π,因而点A'对应的实数是π.
故答案为:π.
14.解:每4个圆周上点就可以有一个内部交点,所以当这些交点不重合的时候,圆内交点最多,
所以,本题等价于将6个点4个分组共有多少组,
显然应该是:=15.
故答案为:15.
15.解:作OE⊥AB于点F,
∵在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.OA=2,
∴∠AOD=90°,∠BOC=30°,OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=OA?tan30°=×=2,AD=4,AB=2AF=2×2×=6,OF=,
∴BD=2,
∴阴影部分的面积是:S△AOD+S扇形OBC﹣S△BDO==+π,
故答案为:
+π.
16.解:设最小的圆的面积是a,则其它三个圆的面积分别是2a,3a,4a,
所有的圆都是相似形,面积的比等于半径的比的平方,
因而半径的比是1:::2,周长的比等于相似比,即半径的比,是1:::2.
故答案为:1:::2.
三.解答题
17.解:由题意得,狗可活动的区域为一个扇形,
此扇形为OAB,圆心角为120°,半径为9m,
故S扇形OAB==27π
答:小狗可活动的区域的面积27π平方米.
18.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.
(2)
∴
∵
∴
∴
即SA:SB=5:6
19.解:设AB=R,AD=r,则有S贴纸=πR2﹣πr2
=π(R2﹣r2)=π(R+r)(R﹣r)=(30+10)×(30﹣10)π=π(cm2);
答:贴纸部分的面积为πcm2.
20.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
21.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
圆的初步认识》单元测试卷
一.选择题
1.过圆上一点可以作出圆的最长弦的条数为( )
A.1条
B.2条
C.3条
D.无数条
2.下列说法正确的是( )
A.长度相等的两条弧是等弧
B.优弧一定大于劣弧
C.不同的圆中不可能有相等的弦
D.直径是弦且同一个圆中最长的弦
3.等于圆周的弧叫做( )
A.劣弧
B.半圆
C.优弧
D.圆
4.下列说法中,不正确的是( )
A.直径是弦,弦是直径
B.半圆周是弧
C.圆上的点到圆心的距离都相等
D.同圆或等圆中,优弧一定比劣弧长
5.已知扇形的半径为6,圆心角为60°,则这个扇形的面积为( )
A.9π
B.6π
C.3π
D.π
6.如图,⊙O的半径为1,分别以⊙O的直径AB上的两个四等分点O1,O2为圆心,为半径作圆,则图中阴影部分的面积为( )
A.π
B.π
C.π
D.2π
7.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA=OB=OC=2,则这朵三叶花的面积为( )
A.3π﹣3
B.3π﹣6
C.6π﹣3
D.6π﹣6
8.三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形EOF的面积为( )
A.π
B.π
C.π
D.π
二.填空题
9.一个扇形的面积是12πcm2,圆心角是60°,则此扇形的半径是
cm.
10.学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花,你认为符合设计要求的图案是
.(将所有符合设计要求的图案序号填上)
11.如图,是两个同心圆,其中两条直径互相垂直,其大圆的半径是2,则其阴影部分的面积之和
(结果保留π).
12.如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是
.
13.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是
.
14.圆周上有6个点,任两点间连一条线段,则这些线段在圆内的交点最多有
个.
15.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为
.
16.把一个圆心为O,半径为r的小圆面积增加一倍,两倍,三倍,分别得到如图所示的四个圆(包括原来的小圆),则这四个圆的周长之比(按从小到大顺序排列)是
.
三.解答题
17.如图,墙OA、OB的夹角∠AOB=120°,一根9米长的绳子一端栓在墙角O处,另一端栓着一只小狗,求小狗可活动的区域的面积.(结果保留π)
18.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
19.如图扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,求贴纸部分的面积.
20.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
21.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
参考答案与试题解析
一.选择题
1.解:圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选:A.
2.解:A、等弧指的是在同圆或等圆中,能够互相重合的弧,而不是长度相等,就一定能够重合,故错误;
B、不在同圆或等圆中,故错误;
C、等弦即只要长度相等即可,故错误;
D、正确.
故选:D.
3.解:根据直径所对的两条弧是半圆,大于半圆的弧是优弧,则等于圆周的弧叫做优弧.
故选:C.
4.解:A、直径是圆内最长的弦,但弦不一定是直径,故本选项错误;
B、半圆周是圆弧,故本选项正确;
C、圆上的点到圆心的距离都等于半径,故本选项正确;
D、同圆中,优弧是大于半圆的弧,而劣弧是小于半圆的弧,故本选项正确.
故选:A.
5.解:∵扇形的半径为6cm,圆心角为60°,
∴S==6π.
故选:B.
6.解:π×12×
=π×1×
=π.
答:图中阴影部分的面积为π.
故选:B.
7.解:如图所示:弧OA是⊙M上满足条件的一段弧,连接AM、MO,
由题意知:∠AMO=90°,AM=OM
∵AO=2,∴AM=.
∵S扇形AMO=×π×MA2=.
S△AMO=AM?MO=1,
∴S弓形AO=﹣1,
∴S三叶花=6×(﹣1)
=3π﹣6.
故选:B.
8.解:连接OC,
由勾股定理得:OC==,
由正方形的性质得:∠EOB=45°,
所以扇形EOF的面积为:=π,
故选:A.
二.填空题
9.解:设这个扇形的半径是rcm.
根据扇形面积公式,得=12π,
解得r=±6(负值舍去).
故答案为6.
10.解:②③④符合要求.
11.解:由题意得,阴影部分的面积之和正好是半圆,则阴影部分的面积之和2π.
12.解:连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=AB=2,四边形DMCN是正方形,DM=.
则扇形FDE的面积是:=π.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
在△DMG和△DNH中,
,
∴△DMG≌△DNH(AAS),
∴S四边形DGCH=S四边形DMCN=2.
则阴影部分的面积是:π﹣2.
故答案为:π﹣2.
13.解:将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A'重合,则转过的距离是圆的周长是π,因而点A'对应的实数是π.
故答案为:π.
14.解:每4个圆周上点就可以有一个内部交点,所以当这些交点不重合的时候,圆内交点最多,
所以,本题等价于将6个点4个分组共有多少组,
显然应该是:=15.
故答案为:15.
15.解:作OE⊥AB于点F,
∵在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.OA=2,
∴∠AOD=90°,∠BOC=30°,OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=OA?tan30°=×=2,AD=4,AB=2AF=2×2×=6,OF=,
∴BD=2,
∴阴影部分的面积是:S△AOD+S扇形OBC﹣S△BDO==+π,
故答案为:
+π.
16.解:设最小的圆的面积是a,则其它三个圆的面积分别是2a,3a,4a,
所有的圆都是相似形,面积的比等于半径的比的平方,
因而半径的比是1:::2,周长的比等于相似比,即半径的比,是1:::2.
故答案为:1:::2.
三.解答题
17.解:由题意得,狗可活动的区域为一个扇形,
此扇形为OAB,圆心角为120°,半径为9m,
故S扇形OAB==27π
答:小狗可活动的区域的面积27π平方米.
18.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.
(2)
∴
∵
∴
∴
即SA:SB=5:6
19.解:设AB=R,AD=r,则有S贴纸=πR2﹣πr2
=π(R2﹣r2)=π(R+r)(R﹣r)=(30+10)×(30﹣10)π=π(cm2);
答:贴纸部分的面积为πcm2.
20.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
21.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
