七年级数学上册试题 第二单元有理数测试卷-苏科版(word版含答案)
文档属性
| 名称 | 七年级数学上册试题 第二单元有理数测试卷-苏科版(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 390.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 19:01:22 | ||
图片预览



文档简介
第二单元测试卷
一、选择题
1.负数的引入是数学发展史上的一大飞跃,使数的家族得到了扩张,为人们认识世界提供了更多的工具.中国是世界上最早认识和应用负数的国家,比西方早一千多年,负数最早记载于下列哪部著作中(
)
A.
B.
C.
D.
2.数轴的原型来源于生活实际,数轴体现了(
)的数学思想,是我们学习和研究有理数的重要工具.
A.整体
B.方程
C.转化
D.数形结合
3.某种芯片每个探针单元的面积为,0.00000164用科学记数法可表示为(
)
A.
B.
C.
D.
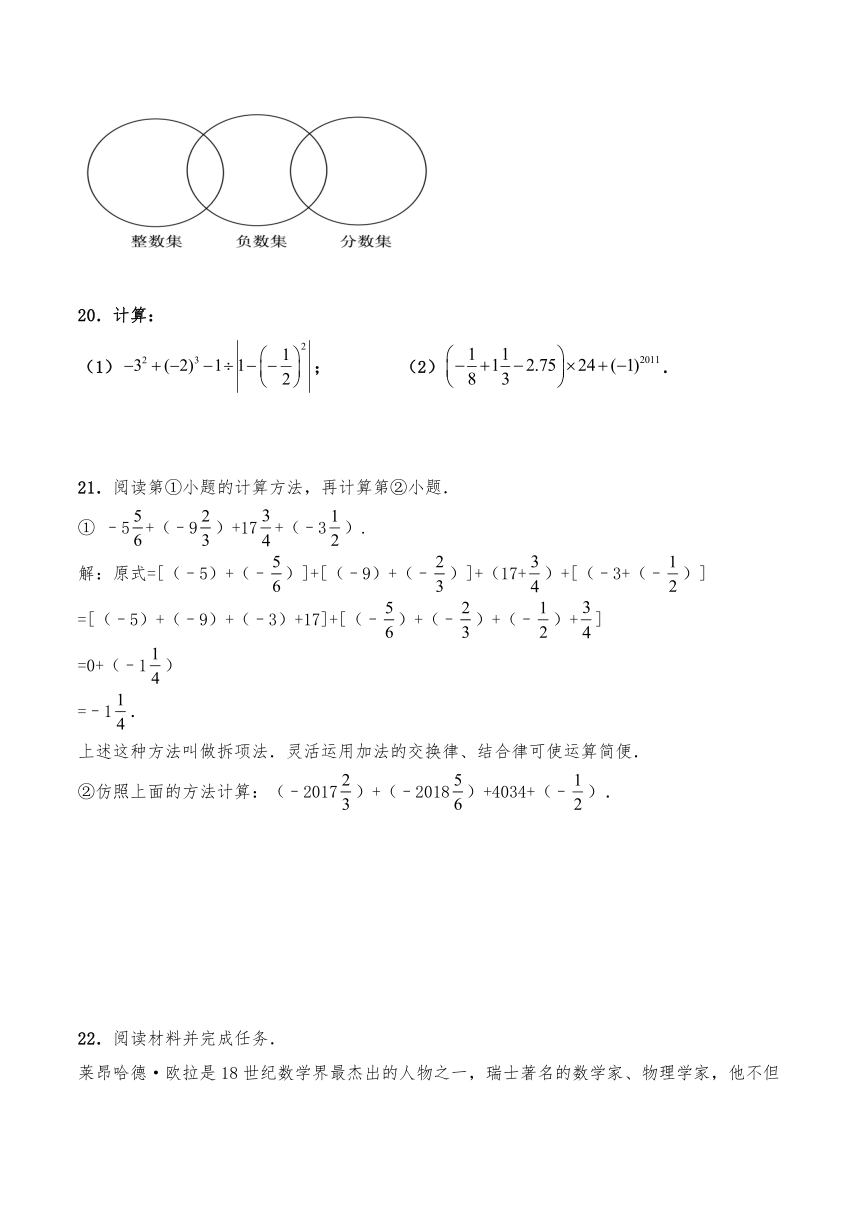
4.如图,关于、、这三部分数集的个数,下列说法正确的是(
)
A.、两部分有无数个,部分只有一个0
B.、、三部分有无数个
C.、、三部分都只有一个
D.部分只有一个,、两部分有无数个
5.下列说法:①
平方等于64的数是8;②
若a,b互为相反数,ab≠0,则;③
若,则的值为负数;④
若ab≠0,则的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为(
)
A.0个
B.1个
C.2个
D.3个
6.(2019·江西省大吉山中学初一期末)当使用计算器的键,将的结果切换成小数格式19.16666667,则对应这个结果19.16666667,以下说法错误的是( )
A.它不是准确值
B.它是一个估算结果
C.它是四舍五入得到的
D.它是一个近似数
7.设n是自然数,则的值为(
)
A.1
B.-1
C.0
D.1或-1
8.如图,数轴上A,B两点所表示的数互为倒数,则关于原点的说法正确的是( )
A.一定在点A的左侧
B.一定与线段AB的中点重合
C.可能在点B的右侧
D.一定与点A或点B重合
9.)“!”是一种运算符号,并且1!=1,2!=1×2,3!=1×2×3,4!=1×2×3×4,
则的值是(
)
A.1
B.2016
C.2017
D.2018
10.数32019?72020?132021的个位数是
( )
A.1
B.3
C.7
D.9
11.有一张厚度为0.1毫米的纸片,对折1次后的厚度是毫米,继续对折,2次,3次,4次……假设这张纸对折了20次,那么此时的厚度相当于每层高3米的楼房层数约是(
)(参考数据:,
)
A.3层
B.20层
C.35层
D.350层
12.若a,b为有理数,下列判断正确的个数是(
)
(1)总是正数;(2)总是正数;(3)的最大值为5;(4)的最大值是3.
A.1
B.2
C.3
D.4
二、填空题
13.若,则m+2n的值是______。
14.已知、两数在数轴上的位置如图所示,则化简代数式的结果是____.
15.已知是有理数,表示不超过的最大整数,如,,,等,那么______.
16.现有七个数将它们填人图(个圆两两相交分成个部分)中,使得每个圆内部的个数之积相等,设这个积为,如图给出了一种填法,此时__________,在所有的填法中,的最大值为__________.
17.满足
的整数
a
的有
个。
18.容器中有A,B,C
3种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子.现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:①最后一颗粒子可能是A粒子;②最后一颗粒子一定是C粒子;③最后一颗粒子一定不是B粒子;④以上都不正确;其中正确结论的序号是
.(写出所有正确结论的序号)
三、解答题
19.把下列各数填入相应的集合的括号内.
,1,-1.5,,0,,-(+8),-7,0.38,|-2|,-20%.
20.计算:
(1);
(2).
21.阅读第①小题的计算方法,再计算第②小题.
①
–5+(–9)+17+(–3).
解:原式=[(–5)+(–)]+[(–9)+(–)]+(17+)+[(–3+(–)]
=[(–5)+(–9)+(–3)+17]+[(–)+(–)+(–)+]
=0+(–1)
=–1.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(–2017)+(–2018)+4034+(–).
22.阅读材料并完成任务.
莱昂哈德·欧拉是18世纪数学界最杰出的人物之一,瑞士著名的数学家、物理学家,他不但为数学界作出贡献,更把整个数学推至物理的领域;同时,也是数学史上研究成果最多的数学家,平均每年写出八百多页的论文,还写了大量的力分析几何学等的课本,《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作.因此,被称为历史上最伟大的两位数学家之一(另一位是卡尔·弗里德里克·高斯).在数学成就上,欧拉最先把关于的多项式用记号的形式来表示(可用其他字母代替,但不同的字母表示不同的多项式),例如,当时,多项式的值用来表示,即;当时,多项式的值用来表示,记为.
任务:已知;.
请你根据材料中代入求值的方法解决下列问题:(1)求的值;(2)求的值.
23.先阅读下列材料,然后解答问题:
材料1:从三张不同的卡片中选出两张排成一列,有6种不同的排法,抽象成数学问题就是从3个不同的元素中选取2个元素的排列,排列数记为A32=3×2=6.
一般地,从n个不同的元素中选取m个元素的排列数记作Anm.
Anm=n(n﹣1)(n﹣2)(n﹣3)…(n﹣m+1)(m≤n)
例:从5个不同的元素中选取3个元素排成一列的排列数为:A53=5×4×3=60.
材料2:从三张不同的卡片中选取两张,有3种不同的选法,抽象成数学问题就是从3个元素中选取2个元素的组合,组合数为.
一般地,从n个不同的元素中取出m个元素的组合数记作Cnm,
Cnm=(m≤n)
例:从6个不同的元素选3个元素的组合数为:.
问:(1)从某个学习小组8人中选取3人参加活动,有
种不同的选法;
(2)从7个人中选取4人,排成一列,有多少种不同的排法.
24.阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是
,数轴上表示﹣2和3的两点之间的距离是
;
(2)数轴上表示x和﹣1的两点之间的距离表示为
;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
25.观察下列式子:;;;将这三个式子相加得到.
(1)猜想并写出:______
(2)直接写出下列各式的计算结果:
①______
②______
(3)探究并计算:
答案
一、选择题
1.C
2.D
3.B
4.A
5.B
6.B
7.D.
8.C
9.D
10.A.
11.C
12.B
二、填空题
13.-1
14.
15..
16.64
256
17.4
18.①③.
三、解答题
19.解:如图所示:
20.
(1);
(2).
21.解:原式=(﹣2017﹣)+(﹣2018﹣)+4034+(﹣)
=(﹣2017﹣2018+4034)+(﹣﹣﹣)
=(﹣1)+(﹣2)
=﹣3.
22.解:(1)将代入中得到:
,故答案为:3.
(2)
将代入中得到:
==.
故答案为:.
23.解:(1)从某个学习小组8人中选取3人参加活动,有:;
(2)从7个人中选取4人,排成一列,有:;
24.(1)|1﹣(﹣3)|=4;|3﹣(﹣2)|=5;故答案为:4;5;
(2)|x﹣(﹣1)|=|x+1|或|(﹣1)﹣x|=|x+1|,故答案为:|x+1|;
(3)有最小值,
当x<﹣3时,|x﹣2|+|x+3|=2﹣x﹣x﹣3=﹣2x﹣1,
当﹣3≤x≤2时,|x﹣2|+|x+3|=2﹣x+x+3=5,
当x>2时,|x﹣2|+|x+3|=x﹣2+x+3=2x+1,
在数轴上|x﹣2|+|x+3|的几何意义是:表示有理数x的点到﹣3及到2的距离之和,所以当﹣3≤x≤2时,它的最小值为5.
25.(1)由题意可得,,故填;
(2)①
=
=
=;
②
=
=
=;
(3)
=
=
=.
一、选择题
1.负数的引入是数学发展史上的一大飞跃,使数的家族得到了扩张,为人们认识世界提供了更多的工具.中国是世界上最早认识和应用负数的国家,比西方早一千多年,负数最早记载于下列哪部著作中(
)
A.
B.
C.
D.
2.数轴的原型来源于生活实际,数轴体现了(
)的数学思想,是我们学习和研究有理数的重要工具.
A.整体
B.方程
C.转化
D.数形结合
3.某种芯片每个探针单元的面积为,0.00000164用科学记数法可表示为(
)
A.
B.
C.
D.
4.如图,关于、、这三部分数集的个数,下列说法正确的是(
)
A.、两部分有无数个,部分只有一个0
B.、、三部分有无数个
C.、、三部分都只有一个
D.部分只有一个,、两部分有无数个
5.下列说法:①
平方等于64的数是8;②
若a,b互为相反数,ab≠0,则;③
若,则的值为负数;④
若ab≠0,则的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为(
)
A.0个
B.1个
C.2个
D.3个
6.(2019·江西省大吉山中学初一期末)当使用计算器的键,将的结果切换成小数格式19.16666667,则对应这个结果19.16666667,以下说法错误的是( )
A.它不是准确值
B.它是一个估算结果
C.它是四舍五入得到的
D.它是一个近似数
7.设n是自然数,则的值为(
)
A.1
B.-1
C.0
D.1或-1
8.如图,数轴上A,B两点所表示的数互为倒数,则关于原点的说法正确的是( )
A.一定在点A的左侧
B.一定与线段AB的中点重合
C.可能在点B的右侧
D.一定与点A或点B重合
9.)“!”是一种运算符号,并且1!=1,2!=1×2,3!=1×2×3,4!=1×2×3×4,
则的值是(
)
A.1
B.2016
C.2017
D.2018
10.数32019?72020?132021的个位数是
( )
A.1
B.3
C.7
D.9
11.有一张厚度为0.1毫米的纸片,对折1次后的厚度是毫米,继续对折,2次,3次,4次……假设这张纸对折了20次,那么此时的厚度相当于每层高3米的楼房层数约是(
)(参考数据:,
)
A.3层
B.20层
C.35层
D.350层
12.若a,b为有理数,下列判断正确的个数是(
)
(1)总是正数;(2)总是正数;(3)的最大值为5;(4)的最大值是3.
A.1
B.2
C.3
D.4
二、填空题
13.若,则m+2n的值是______。
14.已知、两数在数轴上的位置如图所示,则化简代数式的结果是____.
15.已知是有理数,表示不超过的最大整数,如,,,等,那么______.
16.现有七个数将它们填人图(个圆两两相交分成个部分)中,使得每个圆内部的个数之积相等,设这个积为,如图给出了一种填法,此时__________,在所有的填法中,的最大值为__________.
17.满足
的整数
a
的有
个。
18.容器中有A,B,C
3种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗B粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子.例如,一颗A粒子和一颗B粒子发生碰撞则变成一颗C粒子.现有A粒子10颗,B粒子8颗,C粒子9颗,如果经过各种两两碰撞后,只剩1颗粒子.给出下列结论:①最后一颗粒子可能是A粒子;②最后一颗粒子一定是C粒子;③最后一颗粒子一定不是B粒子;④以上都不正确;其中正确结论的序号是
.(写出所有正确结论的序号)
三、解答题
19.把下列各数填入相应的集合的括号内.
,1,-1.5,,0,,-(+8),-7,0.38,|-2|,-20%.
20.计算:
(1);
(2).
21.阅读第①小题的计算方法,再计算第②小题.
①
–5+(–9)+17+(–3).
解:原式=[(–5)+(–)]+[(–9)+(–)]+(17+)+[(–3+(–)]
=[(–5)+(–9)+(–3)+17]+[(–)+(–)+(–)+]
=0+(–1)
=–1.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(–2017)+(–2018)+4034+(–).
22.阅读材料并完成任务.
莱昂哈德·欧拉是18世纪数学界最杰出的人物之一,瑞士著名的数学家、物理学家,他不但为数学界作出贡献,更把整个数学推至物理的领域;同时,也是数学史上研究成果最多的数学家,平均每年写出八百多页的论文,还写了大量的力分析几何学等的课本,《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作.因此,被称为历史上最伟大的两位数学家之一(另一位是卡尔·弗里德里克·高斯).在数学成就上,欧拉最先把关于的多项式用记号的形式来表示(可用其他字母代替,但不同的字母表示不同的多项式),例如,当时,多项式的值用来表示,即;当时,多项式的值用来表示,记为.
任务:已知;.
请你根据材料中代入求值的方法解决下列问题:(1)求的值;(2)求的值.
23.先阅读下列材料,然后解答问题:
材料1:从三张不同的卡片中选出两张排成一列,有6种不同的排法,抽象成数学问题就是从3个不同的元素中选取2个元素的排列,排列数记为A32=3×2=6.
一般地,从n个不同的元素中选取m个元素的排列数记作Anm.
Anm=n(n﹣1)(n﹣2)(n﹣3)…(n﹣m+1)(m≤n)
例:从5个不同的元素中选取3个元素排成一列的排列数为:A53=5×4×3=60.
材料2:从三张不同的卡片中选取两张,有3种不同的选法,抽象成数学问题就是从3个元素中选取2个元素的组合,组合数为.
一般地,从n个不同的元素中取出m个元素的组合数记作Cnm,
Cnm=(m≤n)
例:从6个不同的元素选3个元素的组合数为:.
问:(1)从某个学习小组8人中选取3人参加活动,有
种不同的选法;
(2)从7个人中选取4人,排成一列,有多少种不同的排法.
24.阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是
,数轴上表示﹣2和3的两点之间的距离是
;
(2)数轴上表示x和﹣1的两点之间的距离表示为
;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
25.观察下列式子:;;;将这三个式子相加得到.
(1)猜想并写出:______
(2)直接写出下列各式的计算结果:
①______
②______
(3)探究并计算:
答案
一、选择题
1.C
2.D
3.B
4.A
5.B
6.B
7.D.
8.C
9.D
10.A.
11.C
12.B
二、填空题
13.-1
14.
15..
16.64
256
17.4
18.①③.
三、解答题
19.解:如图所示:
20.
(1);
(2).
21.解:原式=(﹣2017﹣)+(﹣2018﹣)+4034+(﹣)
=(﹣2017﹣2018+4034)+(﹣﹣﹣)
=(﹣1)+(﹣2)
=﹣3.
22.解:(1)将代入中得到:
,故答案为:3.
(2)
将代入中得到:
==.
故答案为:.
23.解:(1)从某个学习小组8人中选取3人参加活动,有:;
(2)从7个人中选取4人,排成一列,有:;
24.(1)|1﹣(﹣3)|=4;|3﹣(﹣2)|=5;故答案为:4;5;
(2)|x﹣(﹣1)|=|x+1|或|(﹣1)﹣x|=|x+1|,故答案为:|x+1|;
(3)有最小值,
当x<﹣3时,|x﹣2|+|x+3|=2﹣x﹣x﹣3=﹣2x﹣1,
当﹣3≤x≤2时,|x﹣2|+|x+3|=2﹣x+x+3=5,
当x>2时,|x﹣2|+|x+3|=x﹣2+x+3=2x+1,
在数轴上|x﹣2|+|x+3|的几何意义是:表示有理数x的点到﹣3及到2的距离之和,所以当﹣3≤x≤2时,它的最小值为5.
25.(1)由题意可得,,故填;
(2)①
=
=
=;
②
=
=
=;
(3)
=
=
=.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
