《作业推荐》高中数学人教A版(2019) 必修(第二册)练习:第十章检测题综合篇(Word版含解析)
文档属性
| 名称 | 《作业推荐》高中数学人教A版(2019) 必修(第二册)练习:第十章检测题综合篇(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 142.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 20:56:03 | ||
图片预览




文档简介
1071880011125200《作业推荐》—第十章检测题综合篇
一、单选题(共 30 分)
1.在试验:连续射击一个目标10次,观察命中的次数中,事件A=“至少命中6次”,则下列说法正确的是( )
A.样本空间中共有10个样本点
B.事件A中有6个样本点
C.样本点6在事件A内
D.事件A中包含样本点11
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A.对立事件 B.不可能事件
C.互斥但不对立事件 D.不是互斥事件
3.下列概率模型中,古典概型的个数为( )
①从区间[1,10]内任取一个数,求取到1的概率;
②从1,2,…,9,10中任取一个整数,求取到1的概率;
③向正方形ABCD内任意投一点P,求点P刚好与点A重合的概率;
④抛掷一枚质地不均匀的骰子,求向上点数为3的概率.
A.1 B.2 C.3 D.4
4.某校高三年级有男生410人,学号为001,002,?,410;女生290人,学号为411,412,?,700.对高三学生进行问卷调查,按学号采用系统抽样的方法,从这700名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为030);再从这10名学生中随机抽取3人进行数据分析,则这3人中既有男生又有女生的概率是( )
A.15 B.310 C.710 D.45
5.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数fx=x2+2ax+4至多有一个零点的概率为( )
A.13 B.12 C.23 D.56
6.下列事件是随机事件的是( )
①当x≥10时,lgx≥1;
②当x∈R,x2+1=0有解;
③当a∈R,关于x的方程x2+a=0在实数集内有解;
④当sinα>sinβ时,α>β.
A.①② B.②③ C.③④ D.①④
7.在半径为R的圆中随机地撒一大把豆子,则豆子落在圆内接正方形中的概率为( )
A.2π B.1π C.2π D.3π
8.甲、乙、丙三位同学独立地解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为12,13,14,则有人能够解决这个问题的概率为( )
A.34 B.13 C.14 D.124
9.下列命题中不正确的是( )
A.根据古典概型概率计算公式P(A)=nAn求出的值是事件A发生的概率的精确值
B.根据古典概型试验,用计算机或计算器产生随机整数统计试验次数N和事件A发生的次数N1,得到的值N1N是P(A)的近似值
C.频率是随机的,在试验前不能确定,随着试验次数的增加,频率会越来越接近概率
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可性相同
10.渝康码是腾讯和支付宝与重庆市政府合作推出的重庆电子健康码,用户申请使用渝康码,凭此码出入小区,学校,医院,商业,公共交通,办公楼宇,交通卡口等.如图,健康人员的渝康码是黑白相间的.已知某个重庆市民的渝康码是边长为15cm的正方形,利用随机模拟的方法向该渝康码内投入900个点,其中落入黑色部分的点的个数为480个,则该渝康码的黑色部分的面积约为( )cm2.
A.105 B.115 C.120 D.135
二、填空题(共 20 分)
11.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是________.
12.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是____________.
13.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为m,n,则“m>2n”的概率是____________.
14.从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是_____.
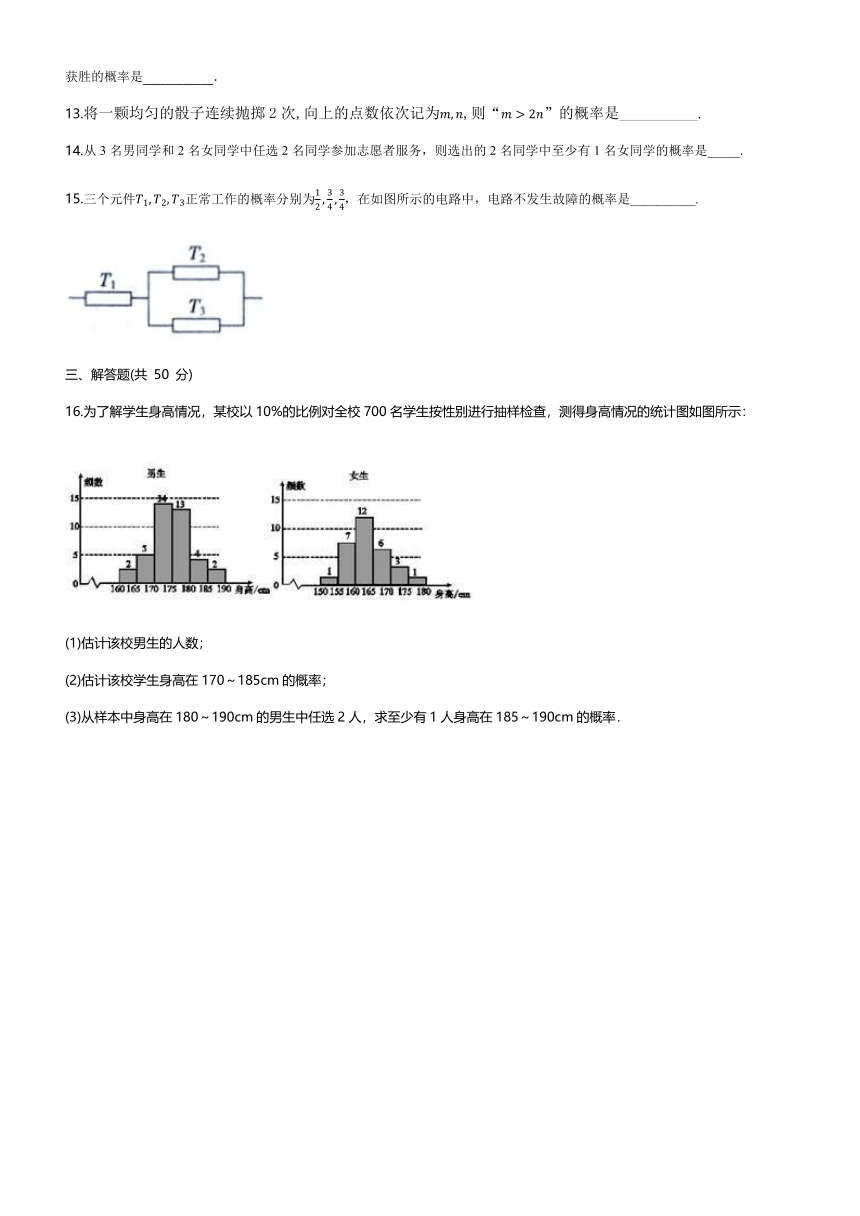
15.三个元件T1,T2,T3正常工作的概率分别为12,34,34,在如图所示的电路中,电路不发生故障的概率是__________.
三、解答题(共 50 分)
16.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
17.某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若xy≤3,则奖励玩具一个;
②若xy≥8,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
18.2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
项目
员工
A
B
C
D
E
F
子女教育
○
○
×
○
×
○
继续教育
×
×
○
×
○
○
大病医疗
×
×
×
○
×
×
住房贷款利息
○
○
×
×
○
○
住房租金
×
×
○
×
×
×
赡养老人
○
○
×
×
×
○
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
1071880011125200《作业推荐》—第十章检测题综合篇
一、单选题(共 30 分)
1.在试验:连续射击一个目标10次,观察命中的次数中,事件A=“至少命中6次”,则下列说法正确的是( )
A.样本空间中共有10个样本点
B.事件A中有6个样本点
C.样本点6在事件A内
D.事件A中包含样本点11
【答案】C
【解析】
【分析】
连续射击一个目标10次,可能全部脱靶,最好的情况是全部命中,故有11个样本点;事件A={6,7,8,9,10},由此判断选项。
【详解】
解析:样本空间中有11个样本点,故A错;事件A中有5个样本点,故B错;样本点中没有11,故D错.
故选:C
【点睛】
注意11个样本点,表示样本空间中有11个元素;样本点11,表示11这个数在样本空间中,两者不是同一概念。
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A.对立事件 B.不可能事件
C.互斥但不对立事件 D.不是互斥事件
【答案】C
【解析】
甲、乙不能同时得到红色,因而这两个事件是互斥事件;又甲、乙可能都得不到红色,即“甲或乙分得红色”的事件不是必然事件,故这两个事件不是对立事件.选C.
3.下列概率模型中,古典概型的个数为( )
①从区间[1,10]内任取一个数,求取到1的概率;
②从1,2,…,9,10中任取一个整数,求取到1的概率;
③向正方形ABCD内任意投一点P,求点P刚好与点A重合的概率;
④抛掷一枚质地不均匀的骰子,求向上点数为3的概率.
A.1 B.2 C.3 D.4
【答案】A
【解析】
【分析】
根据古典概型的特点,逐个判断,即可得出结果.
【详解】
古典概型的特点是样本点的个数是有限的,并且每个样本点发生的可能性相等.
①和③中的样本点是无限的,④中的骰子不均句,不具有等可能性,故只有②是古典概型.
故选:A.
【点睛】
本题主要考查古典概型的判断,熟记古典概型的特点即可,属于基础题型.
4.某校高三年级有男生410人,学号为001,002,?,410;女生290人,学号为411,412,?,700.对高三学生进行问卷调查,按学号采用系统抽样的方法,从这700名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为030);再从这10名学生中随机抽取3人进行数据分析,则这3人中既有男生又有女生的概率是( )
A.15 B.310 C.710 D.45
【答案】D
【解析】
【分析】
利用系统抽样可知,这10个人中男生有6人,女生有4人,计算出所抽3人全是男生或女生的概率,利用对立事件的概率公式可计算出结果.
【详解】
利用系统抽样从这700名学生中抽取10人进行问卷调查,分段间隔为70,
由于第一组抽到的号码为030,所抽取的10人号码依次为030、100、170、240、310、380、450、520、590、660,其中男生6人,女生4人,
因此,从这10名学生中随机抽取3人进行数据分析,则这3人中既有男生又有女生的概率是P=1?C43+C63C103=45.
故选:D.
【点睛】
本题考查古典概型概率的计算,考查了系统抽样、组合计数原理以及对立事件概率公式的应用,考查计算能力,属于中等题.
5.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数fx=x2+2ax+4至多有一个零点的概率为( )
A.13 B.12 C.23 D.56
【答案】A
【解析】
【分析】
由函数fx至多有一个零点,求得?2≤a≤2,得到a的取值有1,2,共2个可能结果,结合古典概型及概率的计算公式,即可求解.
【详解】
由题意,抛掷一枚质地的均匀的骰子,正面向上的点数包含6个可能结果,
又由函数fx=x2+2ax+4至多有一个零点,则Δ=4a2?16≤0,解得?2≤a≤2,
又因为a为正整数,故a的取值有1,2,共2个可能结果,
所以函数fx=x2+2ax+4至多有一个零点的概率为13.
故选:A.
【点睛】
本题主要考查的是古典概型及其概率计算公式,解题时准确找出试验包含的基本事件的个数,求得函数至多一个零点所包含的的个数,利用古典概型及其概率的计算公式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
6.下列事件是随机事件的是( )
①当x≥10时,lgx≥1;
②当x∈R,x2+1=0有解;
③当a∈R,关于x的方程x2+a=0在实数集内有解;
④当sinα>sinβ时,α>β.
A.①② B.②③ C.③④ D.①④
【答案】C
【解析】
【分析】
根据随机事件的概念对四个事件分别进行分析即可得到结论。
【详解】
对于①,由于x≥10时,lgx≥1恒成立,故事件①为必然事件;
对于②,由于x2+1=0无实数根,故事件②为不可能事件;
对于③,当a∈R,关于x的方程x2+a=0在实数集内可能有解,也可能无解,故事件③为随机事件;
对于④,当sinα>sinβ时,α>β可能成立,也可能不成立,故事件④为随机事件,
综上,事件③④为随机事件.
故选:C.
【点睛】
本题考查对随机事件概念的理解,是基础题。
7.在半径为R的圆中随机地撒一大把豆子,则豆子落在圆内接正方形中的概率为( )
A.2π B.1π C.2π D.3π
【答案】A
【解析】
【分析】
画出图形,假设圆的半径,计算圆内接正方形的边长,根据几何概型的概念,计算正方形与圆的面积之比可得结果.
【详解】
如图
设圆的半径为R,则正方形ABCD边长AB=2R
正方形ABCD面积为S1=2R2=2R2
圆的面积为S2=πR2
则豆子落在圆内接正方形中的概率为S1S2=2R2πR2=2π
故选:A
【点睛】
本题考查几何概型的应用,熟悉几何概型的概念,常见的比例模型:长度之比,面积之比,角度之比,体积之比,属基础题.
8.甲、乙、丙三位同学独立地解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为12,13,14,则有人能够解决这个问题的概率为( )
A.34 B.13 C.14 D.124
【答案】A
【解析】
【分析】
可先求得没有人能解决这个问题的概率, 再根据对立事件的性质求得有人能够解决这个问题的概率即可.
【详解】
“没有人能解决这个问题”的概率为1?12×1?13×1?14=14
所以“有人能解决这个问题”的概率为
1?14=34
故选:A
【点睛】
本题考查了对立事件概率的性质及简单应用,属于基础题.
9.下列命题中不正确的是( )
A.根据古典概型概率计算公式P(A)=nAn求出的值是事件A发生的概率的精确值
B.根据古典概型试验,用计算机或计算器产生随机整数统计试验次数N和事件A发生的次数N1,得到的值N1N是P(A)的近似值
C.频率是随机的,在试验前不能确定,随着试验次数的增加,频率会越来越接近概率
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可性相同
【答案】C
【解析】
【分析】
根据概率的定义以及古典概型概率计算方法逐个选项判断即可.
【详解】
对于A,即古典概型概率计算公式,很明显正确的;
对于B,随机模拟中得到的值是概率的近似值,则B项命题正确;
对于C,频率稳定在某个常数上,这个常数叫做概率,但与概率的趋近程度不是试验次数的函数,C命题不正确;
对于D,5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性都是15,D命题正确;
故选:C.
【点睛】
本题主要以命题的真假判断为载体,考查了概率的基本概念,难度不大,属于基础题.
10.渝康码是腾讯和支付宝与重庆市政府合作推出的重庆电子健康码,用户申请使用渝康码,凭此码出入小区,学校,医院,商业,公共交通,办公楼宇,交通卡口等.如图,健康人员的渝康码是黑白相间的.已知某个重庆市民的渝康码是边长为15cm的正方形,利用随机模拟的方法向该渝康码内投入900个点,其中落入黑色部分的点的个数为480个,则该渝康码的黑色部分的面积约为( )cm2.
A.105 B.115 C.120 D.135
【答案】C
【解析】
【分析】
由几何概型中的面积型结合随机模拟试验,即可求出结果.
【详解】
因为渝康码是边长为15cm的正方形,向该渝康码内投入900个点,
其中落入黑色部分的点的个数为480个,
设该渝康码的黑色部分的面积为x,
则x225=480900?x=120.
故选:C.
【点睛】
本题主要考查了几何概型和用模拟实验的方法估计概率的应用问题,属于基础题.
二、填空题(共 20 分)
11.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是________.
【答案】56
【解析】
基本事件总数为36,点数之和小于10的基本事件共有30种,所以所求概率为3036=56.
【考点】古典概型
【名师点睛】概率问题的考查,侧重于对古典概型和对立事件的概率的考查,属于简单题.江苏对古典概型概率的考查,注重事件本身的理解,淡化计数方法.因此先明确所求事件本身的含义,然后一般利用枚举法、树形图解决计数问题,而当正面问题比较复杂时,往往利用对立事件的概率公式进行求解.
12.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是____________.
【答案】0.18
【解析】
【分析】
本题应注意分情况讨论,即前五场甲队获胜的两种情况,应用独立事件的概率的计算公式求解.题目有一定的难度,注重了基础知识、基本计算能力及分类讨论思想的考查.
【详解】
前四场中有一场客场输,第五场赢时,甲队以4:1获胜的概率是0.63×0.5×0.5×2=0.108,
前四场中有一场主场输,第五场赢时,甲队以4:1获胜的概率是0.4×0.62×0.52×2=0.072,
综上所述,甲队以4:1获胜的概率是q=0.108+0.072=0.18.
【点睛】
由于本题题干较长,所以,易错点之一就是能否静心读题,正确理解题意;易错点之二是思维的全面性是否具备,要考虑甲队以4:1获胜的两种情况;易错点之三是是否能够准确计算.
13.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为m,n,则“m>2n”的概率是____________.
【答案】16
【解析】
分析:骰子连续抛掷2次共有36种结果,满足m>2n的有6种
详解:一颗均匀的骰子连续抛掷2次,向上的点数依次记为m,n,
则共有6×6=36种结果,
满足m>2n共有:(3,1),(4,1),(5,1),(6,1),(5,2),(6,2)6种
则m>2n”的概率是P=636=16
点睛:古典概型概率要准确求出总的事件个数和基本事件个数,然后根据概率公式
P(A)=事件A包含的基本事件个数试验的基本事件总数求解.
14.从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是_____.
【答案】710.
【解析】
【分析】
先求事件的总数,再求选出的2名同学中至少有1名女同学的事件数,最后根据古典概型的概率计算公式得出答案.
【详解】
从3名男同学和2名女同学中任选2名同学参加志愿服务,共有C52=10种情况.
若选出的2名学生恰有1名女生,有C31C21=6种情况,
若选出的2名学生都是女生,有C22=1种情况,
所以所求的概率为6+110=710.
【点睛】
计数原理是高考考查的重点内容,考查的形式有两种,一是独立考查,二是与古典概型结合考查,由于古典概型概率的计算比较明确,所以,计算正确基本事件总数是解题的重要一环.在处理问题的过程中,应注意审清题意,明确“分类”“分步”,根据顺序有无,明确“排列”“组合”.
15.三个元件T1,T2,T3正常工作的概率分别为12,34,34,在如图所示的电路中,电路不发生故障的概率是__________.
【答案】1532
【解析】
【分析】
根据电路图可知, T2与T3并联,再与T1串联.由电路的性质可知,不发生故障,则T1正常工作且T2,T3至少有一个正常工作,即可由独立事件与对立事件的概率性质求解.
【详解】
电路不发生故障为“T1正常工作且T2,T3至少有一个正常工作”
而“T2,T3至少有一个元件正常工作”的对立事件为“T2,T3都不正常工作”
所以电路不发生故障的概率是12×1?1?34×1?34=1532
【点睛】
本题考查了独立事件与对立事件在物理学中的应用,由电路正常工作求事件的概率,属于基础题.
三、解答题(共 50 分)
16.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
【答案】(Ⅰ)400
(Ⅱ)p1=0.5.
(Ⅲ)p2=35
【解析】
试题分析:(1)根据频率分布直方图,求出样本中男生人数,再由分层抽样比例,估计全校男生人数;(2)由统计图计算出样本中身高在170~185cm之间的学生数,根据样本数据计算对应的概率;(3)利用列举法计算基本事件数以及对应的概率
试题解析:(Ⅰ)样本中男生人数为40 ,由分层抽样比例为10%估计全校男生人数为400.
(Ⅱ)由统计图知,样本中身高在170~185cm之间的学生有52人,样本容量为70 ,所以样本中学生身高在170~185cm之间的频率故有估计该校学生身高在170~185cm之间的概率p=
(Ⅲ)样本中身高在180~185cm之间的男生有4人,设其编号为①,②,③,④,
样本中身高在185~190cm之间的男生有2人,设其编号为⑤,⑥,
从上述6人中任取2人的树状图为:
故从样本中身高在180~190cm之间的男生中任选2人的所有可能结果数为15,至少有1人身高在185~190cm之间的可能结果数为9,因此,所求概率p2=915=35
考点:频率分布直方图;古典概型及其概率计算公式
17.某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若xy≤3,则奖励玩具一个;
②若xy≥8,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
【答案】(Ⅰ)516.(Ⅱ)小亮获得水杯的概率大于获得饮料的概率.
【解析】
【分析】
【详解】
(Ⅰ)两次记录的所有结果为(1,1),(1,,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.
满足xy≤3的有(1,1),(1,,2),(1,3),(2,1),(3,1),共5个,所以小亮获得玩具的概率为516.
(Ⅱ) 满足xy≥8的有(2,4),(3,,3),(3,4),(4,2),(4,3),(4,4),共6个,所以小亮获得水杯的概率为616;
小亮获得饮料的概率为1?516?616=516,所以小亮获得水杯的概率大于获得饮料的概率.
18.2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
项目
员工
A
B
C
D
E
F
子女教育
○
○
×
○
×
○
继续教育
×
×
○
×
○
○
大病医疗
×
×
×
○
×
×
住房贷款利息
○
○
×
×
○
○
住房租金
×
×
○
×
×
×
赡养老人
○
○
×
×
×
○
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
【答案】(1)从老、中、青员工中分别抽取6人,9人,10人
(2)①{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},{E,F},共11种 ②1115
【解析】
【分析】
(1)根据分层抽样各层所抽比例相等可得结果;
(2)①用列举法求出基本事件数;
②用列举法求出事件M所含基本事件数以及对应的概率
【详解】
(1)由已知,老、中、青员工人数之比为6:9:10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},共15种.
②由题中表格知,符合题意的所有可能结果为{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},{E,F},共11种.
所以,事件M发生的概率P(M)=1115.
【点睛】
本题考查了用列举法求古典概型的概率问题以及根据数据分析统计结论的问题,属于基础题.
一、单选题(共 30 分)
1.在试验:连续射击一个目标10次,观察命中的次数中,事件A=“至少命中6次”,则下列说法正确的是( )
A.样本空间中共有10个样本点
B.事件A中有6个样本点
C.样本点6在事件A内
D.事件A中包含样本点11
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A.对立事件 B.不可能事件
C.互斥但不对立事件 D.不是互斥事件
3.下列概率模型中,古典概型的个数为( )
①从区间[1,10]内任取一个数,求取到1的概率;
②从1,2,…,9,10中任取一个整数,求取到1的概率;
③向正方形ABCD内任意投一点P,求点P刚好与点A重合的概率;
④抛掷一枚质地不均匀的骰子,求向上点数为3的概率.
A.1 B.2 C.3 D.4
4.某校高三年级有男生410人,学号为001,002,?,410;女生290人,学号为411,412,?,700.对高三学生进行问卷调查,按学号采用系统抽样的方法,从这700名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为030);再从这10名学生中随机抽取3人进行数据分析,则这3人中既有男生又有女生的概率是( )
A.15 B.310 C.710 D.45
5.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数fx=x2+2ax+4至多有一个零点的概率为( )
A.13 B.12 C.23 D.56
6.下列事件是随机事件的是( )
①当x≥10时,lgx≥1;
②当x∈R,x2+1=0有解;
③当a∈R,关于x的方程x2+a=0在实数集内有解;
④当sinα>sinβ时,α>β.
A.①② B.②③ C.③④ D.①④
7.在半径为R的圆中随机地撒一大把豆子,则豆子落在圆内接正方形中的概率为( )
A.2π B.1π C.2π D.3π
8.甲、乙、丙三位同学独立地解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为12,13,14,则有人能够解决这个问题的概率为( )
A.34 B.13 C.14 D.124
9.下列命题中不正确的是( )
A.根据古典概型概率计算公式P(A)=nAn求出的值是事件A发生的概率的精确值
B.根据古典概型试验,用计算机或计算器产生随机整数统计试验次数N和事件A发生的次数N1,得到的值N1N是P(A)的近似值
C.频率是随机的,在试验前不能确定,随着试验次数的增加,频率会越来越接近概率
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可性相同
10.渝康码是腾讯和支付宝与重庆市政府合作推出的重庆电子健康码,用户申请使用渝康码,凭此码出入小区,学校,医院,商业,公共交通,办公楼宇,交通卡口等.如图,健康人员的渝康码是黑白相间的.已知某个重庆市民的渝康码是边长为15cm的正方形,利用随机模拟的方法向该渝康码内投入900个点,其中落入黑色部分的点的个数为480个,则该渝康码的黑色部分的面积约为( )cm2.
A.105 B.115 C.120 D.135
二、填空题(共 20 分)
11.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是________.
12.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是____________.
13.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为m,n,则“m>2n”的概率是____________.
14.从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是_____.
15.三个元件T1,T2,T3正常工作的概率分别为12,34,34,在如图所示的电路中,电路不发生故障的概率是__________.
三、解答题(共 50 分)
16.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
17.某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若xy≤3,则奖励玩具一个;
②若xy≥8,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
18.2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
项目
员工
A
B
C
D
E
F
子女教育
○
○
×
○
×
○
继续教育
×
×
○
×
○
○
大病医疗
×
×
×
○
×
×
住房贷款利息
○
○
×
×
○
○
住房租金
×
×
○
×
×
×
赡养老人
○
○
×
×
×
○
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
1071880011125200《作业推荐》—第十章检测题综合篇
一、单选题(共 30 分)
1.在试验:连续射击一个目标10次,观察命中的次数中,事件A=“至少命中6次”,则下列说法正确的是( )
A.样本空间中共有10个样本点
B.事件A中有6个样本点
C.样本点6在事件A内
D.事件A中包含样本点11
【答案】C
【解析】
【分析】
连续射击一个目标10次,可能全部脱靶,最好的情况是全部命中,故有11个样本点;事件A={6,7,8,9,10},由此判断选项。
【详解】
解析:样本空间中有11个样本点,故A错;事件A中有5个样本点,故B错;样本点中没有11,故D错.
故选:C
【点睛】
注意11个样本点,表示样本空间中有11个元素;样本点11,表示11这个数在样本空间中,两者不是同一概念。
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A.对立事件 B.不可能事件
C.互斥但不对立事件 D.不是互斥事件
【答案】C
【解析】
甲、乙不能同时得到红色,因而这两个事件是互斥事件;又甲、乙可能都得不到红色,即“甲或乙分得红色”的事件不是必然事件,故这两个事件不是对立事件.选C.
3.下列概率模型中,古典概型的个数为( )
①从区间[1,10]内任取一个数,求取到1的概率;
②从1,2,…,9,10中任取一个整数,求取到1的概率;
③向正方形ABCD内任意投一点P,求点P刚好与点A重合的概率;
④抛掷一枚质地不均匀的骰子,求向上点数为3的概率.
A.1 B.2 C.3 D.4
【答案】A
【解析】
【分析】
根据古典概型的特点,逐个判断,即可得出结果.
【详解】
古典概型的特点是样本点的个数是有限的,并且每个样本点发生的可能性相等.
①和③中的样本点是无限的,④中的骰子不均句,不具有等可能性,故只有②是古典概型.
故选:A.
【点睛】
本题主要考查古典概型的判断,熟记古典概型的特点即可,属于基础题型.
4.某校高三年级有男生410人,学号为001,002,?,410;女生290人,学号为411,412,?,700.对高三学生进行问卷调查,按学号采用系统抽样的方法,从这700名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为030);再从这10名学生中随机抽取3人进行数据分析,则这3人中既有男生又有女生的概率是( )
A.15 B.310 C.710 D.45
【答案】D
【解析】
【分析】
利用系统抽样可知,这10个人中男生有6人,女生有4人,计算出所抽3人全是男生或女生的概率,利用对立事件的概率公式可计算出结果.
【详解】
利用系统抽样从这700名学生中抽取10人进行问卷调查,分段间隔为70,
由于第一组抽到的号码为030,所抽取的10人号码依次为030、100、170、240、310、380、450、520、590、660,其中男生6人,女生4人,
因此,从这10名学生中随机抽取3人进行数据分析,则这3人中既有男生又有女生的概率是P=1?C43+C63C103=45.
故选:D.
【点睛】
本题考查古典概型概率的计算,考查了系统抽样、组合计数原理以及对立事件概率公式的应用,考查计算能力,属于中等题.
5.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数fx=x2+2ax+4至多有一个零点的概率为( )
A.13 B.12 C.23 D.56
【答案】A
【解析】
【分析】
由函数fx至多有一个零点,求得?2≤a≤2,得到a的取值有1,2,共2个可能结果,结合古典概型及概率的计算公式,即可求解.
【详解】
由题意,抛掷一枚质地的均匀的骰子,正面向上的点数包含6个可能结果,
又由函数fx=x2+2ax+4至多有一个零点,则Δ=4a2?16≤0,解得?2≤a≤2,
又因为a为正整数,故a的取值有1,2,共2个可能结果,
所以函数fx=x2+2ax+4至多有一个零点的概率为13.
故选:A.
【点睛】
本题主要考查的是古典概型及其概率计算公式,解题时准确找出试验包含的基本事件的个数,求得函数至多一个零点所包含的的个数,利用古典概型及其概率的计算公式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
6.下列事件是随机事件的是( )
①当x≥10时,lgx≥1;
②当x∈R,x2+1=0有解;
③当a∈R,关于x的方程x2+a=0在实数集内有解;
④当sinα>sinβ时,α>β.
A.①② B.②③ C.③④ D.①④
【答案】C
【解析】
【分析】
根据随机事件的概念对四个事件分别进行分析即可得到结论。
【详解】
对于①,由于x≥10时,lgx≥1恒成立,故事件①为必然事件;
对于②,由于x2+1=0无实数根,故事件②为不可能事件;
对于③,当a∈R,关于x的方程x2+a=0在实数集内可能有解,也可能无解,故事件③为随机事件;
对于④,当sinα>sinβ时,α>β可能成立,也可能不成立,故事件④为随机事件,
综上,事件③④为随机事件.
故选:C.
【点睛】
本题考查对随机事件概念的理解,是基础题。
7.在半径为R的圆中随机地撒一大把豆子,则豆子落在圆内接正方形中的概率为( )
A.2π B.1π C.2π D.3π
【答案】A
【解析】
【分析】
画出图形,假设圆的半径,计算圆内接正方形的边长,根据几何概型的概念,计算正方形与圆的面积之比可得结果.
【详解】
如图
设圆的半径为R,则正方形ABCD边长AB=2R
正方形ABCD面积为S1=2R2=2R2
圆的面积为S2=πR2
则豆子落在圆内接正方形中的概率为S1S2=2R2πR2=2π
故选:A
【点睛】
本题考查几何概型的应用,熟悉几何概型的概念,常见的比例模型:长度之比,面积之比,角度之比,体积之比,属基础题.
8.甲、乙、丙三位同学独立地解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为12,13,14,则有人能够解决这个问题的概率为( )
A.34 B.13 C.14 D.124
【答案】A
【解析】
【分析】
可先求得没有人能解决这个问题的概率, 再根据对立事件的性质求得有人能够解决这个问题的概率即可.
【详解】
“没有人能解决这个问题”的概率为1?12×1?13×1?14=14
所以“有人能解决这个问题”的概率为
1?14=34
故选:A
【点睛】
本题考查了对立事件概率的性质及简单应用,属于基础题.
9.下列命题中不正确的是( )
A.根据古典概型概率计算公式P(A)=nAn求出的值是事件A发生的概率的精确值
B.根据古典概型试验,用计算机或计算器产生随机整数统计试验次数N和事件A发生的次数N1,得到的值N1N是P(A)的近似值
C.频率是随机的,在试验前不能确定,随着试验次数的增加,频率会越来越接近概率
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可性相同
【答案】C
【解析】
【分析】
根据概率的定义以及古典概型概率计算方法逐个选项判断即可.
【详解】
对于A,即古典概型概率计算公式,很明显正确的;
对于B,随机模拟中得到的值是概率的近似值,则B项命题正确;
对于C,频率稳定在某个常数上,这个常数叫做概率,但与概率的趋近程度不是试验次数的函数,C命题不正确;
对于D,5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性都是15,D命题正确;
故选:C.
【点睛】
本题主要以命题的真假判断为载体,考查了概率的基本概念,难度不大,属于基础题.
10.渝康码是腾讯和支付宝与重庆市政府合作推出的重庆电子健康码,用户申请使用渝康码,凭此码出入小区,学校,医院,商业,公共交通,办公楼宇,交通卡口等.如图,健康人员的渝康码是黑白相间的.已知某个重庆市民的渝康码是边长为15cm的正方形,利用随机模拟的方法向该渝康码内投入900个点,其中落入黑色部分的点的个数为480个,则该渝康码的黑色部分的面积约为( )cm2.
A.105 B.115 C.120 D.135
【答案】C
【解析】
【分析】
由几何概型中的面积型结合随机模拟试验,即可求出结果.
【详解】
因为渝康码是边长为15cm的正方形,向该渝康码内投入900个点,
其中落入黑色部分的点的个数为480个,
设该渝康码的黑色部分的面积为x,
则x225=480900?x=120.
故选:C.
【点睛】
本题主要考查了几何概型和用模拟实验的方法估计概率的应用问题,属于基础题.
二、填空题(共 20 分)
11.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是________.
【答案】56
【解析】
基本事件总数为36,点数之和小于10的基本事件共有30种,所以所求概率为3036=56.
【考点】古典概型
【名师点睛】概率问题的考查,侧重于对古典概型和对立事件的概率的考查,属于简单题.江苏对古典概型概率的考查,注重事件本身的理解,淡化计数方法.因此先明确所求事件本身的含义,然后一般利用枚举法、树形图解决计数问题,而当正面问题比较复杂时,往往利用对立事件的概率公式进行求解.
12.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是____________.
【答案】0.18
【解析】
【分析】
本题应注意分情况讨论,即前五场甲队获胜的两种情况,应用独立事件的概率的计算公式求解.题目有一定的难度,注重了基础知识、基本计算能力及分类讨论思想的考查.
【详解】
前四场中有一场客场输,第五场赢时,甲队以4:1获胜的概率是0.63×0.5×0.5×2=0.108,
前四场中有一场主场输,第五场赢时,甲队以4:1获胜的概率是0.4×0.62×0.52×2=0.072,
综上所述,甲队以4:1获胜的概率是q=0.108+0.072=0.18.
【点睛】
由于本题题干较长,所以,易错点之一就是能否静心读题,正确理解题意;易错点之二是思维的全面性是否具备,要考虑甲队以4:1获胜的两种情况;易错点之三是是否能够准确计算.
13.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为m,n,则“m>2n”的概率是____________.
【答案】16
【解析】
分析:骰子连续抛掷2次共有36种结果,满足m>2n的有6种
详解:一颗均匀的骰子连续抛掷2次,向上的点数依次记为m,n,
则共有6×6=36种结果,
满足m>2n共有:(3,1),(4,1),(5,1),(6,1),(5,2),(6,2)6种
则m>2n”的概率是P=636=16
点睛:古典概型概率要准确求出总的事件个数和基本事件个数,然后根据概率公式
P(A)=事件A包含的基本事件个数试验的基本事件总数求解.
14.从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是_____.
【答案】710.
【解析】
【分析】
先求事件的总数,再求选出的2名同学中至少有1名女同学的事件数,最后根据古典概型的概率计算公式得出答案.
【详解】
从3名男同学和2名女同学中任选2名同学参加志愿服务,共有C52=10种情况.
若选出的2名学生恰有1名女生,有C31C21=6种情况,
若选出的2名学生都是女生,有C22=1种情况,
所以所求的概率为6+110=710.
【点睛】
计数原理是高考考查的重点内容,考查的形式有两种,一是独立考查,二是与古典概型结合考查,由于古典概型概率的计算比较明确,所以,计算正确基本事件总数是解题的重要一环.在处理问题的过程中,应注意审清题意,明确“分类”“分步”,根据顺序有无,明确“排列”“组合”.
15.三个元件T1,T2,T3正常工作的概率分别为12,34,34,在如图所示的电路中,电路不发生故障的概率是__________.
【答案】1532
【解析】
【分析】
根据电路图可知, T2与T3并联,再与T1串联.由电路的性质可知,不发生故障,则T1正常工作且T2,T3至少有一个正常工作,即可由独立事件与对立事件的概率性质求解.
【详解】
电路不发生故障为“T1正常工作且T2,T3至少有一个正常工作”
而“T2,T3至少有一个元件正常工作”的对立事件为“T2,T3都不正常工作”
所以电路不发生故障的概率是12×1?1?34×1?34=1532
【点睛】
本题考查了独立事件与对立事件在物理学中的应用,由电路正常工作求事件的概率,属于基础题.
三、解答题(共 50 分)
16.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
【答案】(Ⅰ)400
(Ⅱ)p1=0.5.
(Ⅲ)p2=35
【解析】
试题分析:(1)根据频率分布直方图,求出样本中男生人数,再由分层抽样比例,估计全校男生人数;(2)由统计图计算出样本中身高在170~185cm之间的学生数,根据样本数据计算对应的概率;(3)利用列举法计算基本事件数以及对应的概率
试题解析:(Ⅰ)样本中男生人数为40 ,由分层抽样比例为10%估计全校男生人数为400.
(Ⅱ)由统计图知,样本中身高在170~185cm之间的学生有52人,样本容量为70 ,所以样本中学生身高在170~185cm之间的频率故有估计该校学生身高在170~185cm之间的概率p=
(Ⅲ)样本中身高在180~185cm之间的男生有4人,设其编号为①,②,③,④,
样本中身高在185~190cm之间的男生有2人,设其编号为⑤,⑥,
从上述6人中任取2人的树状图为:
故从样本中身高在180~190cm之间的男生中任选2人的所有可能结果数为15,至少有1人身高在185~190cm之间的可能结果数为9,因此,所求概率p2=915=35
考点:频率分布直方图;古典概型及其概率计算公式
17.某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若xy≤3,则奖励玩具一个;
②若xy≥8,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
【答案】(Ⅰ)516.(Ⅱ)小亮获得水杯的概率大于获得饮料的概率.
【解析】
【分析】
【详解】
(Ⅰ)两次记录的所有结果为(1,1),(1,,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.
满足xy≤3的有(1,1),(1,,2),(1,3),(2,1),(3,1),共5个,所以小亮获得玩具的概率为516.
(Ⅱ) 满足xy≥8的有(2,4),(3,,3),(3,4),(4,2),(4,3),(4,4),共6个,所以小亮获得水杯的概率为616;
小亮获得饮料的概率为1?516?616=516,所以小亮获得水杯的概率大于获得饮料的概率.
18.2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
项目
员工
A
B
C
D
E
F
子女教育
○
○
×
○
×
○
继续教育
×
×
○
×
○
○
大病医疗
×
×
×
○
×
×
住房贷款利息
○
○
×
×
○
○
住房租金
×
×
○
×
×
×
赡养老人
○
○
×
×
×
○
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
【答案】(1)从老、中、青员工中分别抽取6人,9人,10人
(2)①{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},{E,F},共11种 ②1115
【解析】
【分析】
(1)根据分层抽样各层所抽比例相等可得结果;
(2)①用列举法求出基本事件数;
②用列举法求出事件M所含基本事件数以及对应的概率
【详解】
(1)由已知,老、中、青员工人数之比为6:9:10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},共15种.
②由题中表格知,符合题意的所有可能结果为{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},{E,F},共11种.
所以,事件M发生的概率P(M)=1115.
【点睛】
本题考查了用列举法求古典概型的概率问题以及根据数据分析统计结论的问题,属于基础题.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
