《作业推荐》高中数学人教A版(2019) 必修(第二册)同步练习:9.2用样本估计总体之抽样的数字特征的计算练习(Word版含解析)
文档属性
| 名称 | 《作业推荐》高中数学人教A版(2019) 必修(第二册)同步练习:9.2用样本估计总体之抽样的数字特征的计算练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 402.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览



文档简介
1188720012331700《作业推荐》—9.2用样本估计总体之抽样的数字特征的计算练习
一、单选题(共 65 分)
1.某老师从星期一到星期五收到的信件数分别为10,6,8, 5, 6,则该组数据的方差s2的值为( )
A.455 B.45 C.165 D.16
2.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )
A.0.5 B.0.6 C.0.7 D.0.8
3.已知一组数据x1、x2、x3、x4、x5的平均数是2,方差是13,那么另一组数3x1?2、3x2?2、3x3?2、3x4?2、3x5?2的平均数,方差分别是( )
A.2,13 B.2,1 C.4,3 D.4,23
4.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
5.某校高一学生进行测试,随机抽取20名学生的测试成绩,绘制茎叶图如图所示,则这组数据的中位数和众数分别为( )
A.86,77 B.86,78 C.77,77 D.78,86
6.在某次赛车中,50名参赛选手的成绩(单位:min)全部介于13到18之间(包括13和18),将比赛成绩分为五组:第一组[13,14),第二组[14,15),··· ,第五组[17,18],其频率分布直方图如图所示.若成绩在[13,15)内的选手可获奖,则这50名选手中获奖的人数为( )
A.11 B.15 C.35 D.39
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
8.如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
①深圳的变化幅度最小,北京的平均价格最高;
②深圳和度厦门往返机票的平均价格同去年相比有所下降;
③平均价格从高到低位于前三位的城市为北京,深圳,广州;
④平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
10.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
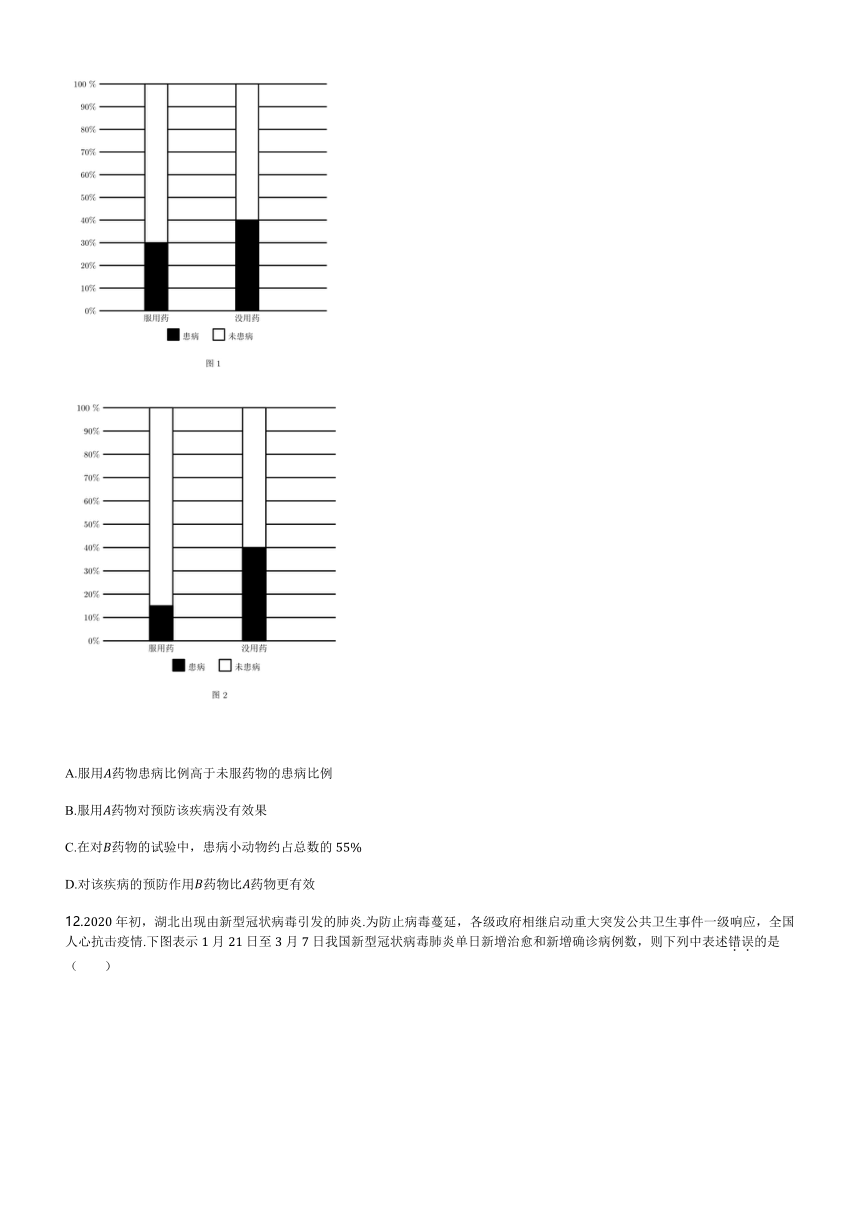
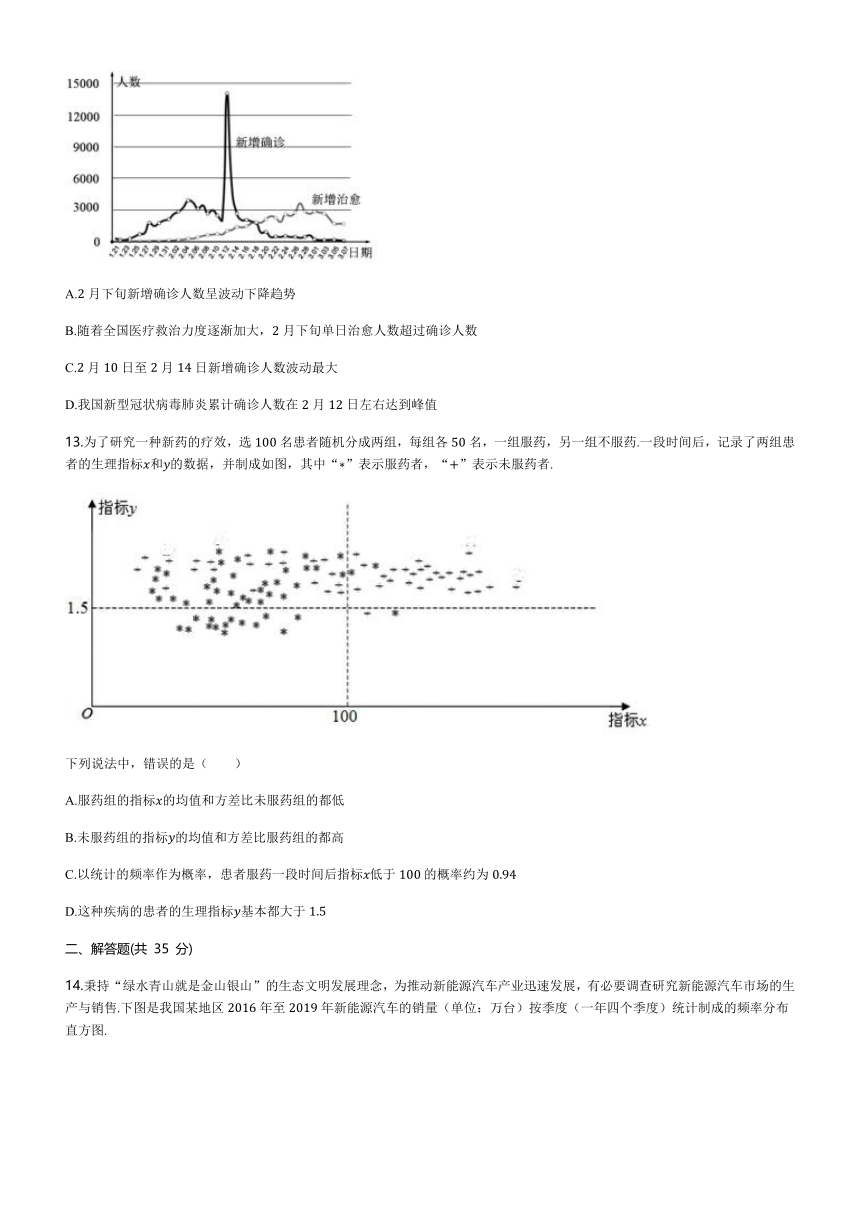
11.为了考察A、B两种药物预防某种疾病的效果,某研究所进行动物试验,已知参与两种药物试验的服药和未服药的动物数量相同,图1是A药试验结果对应的等高条形图;图2是B药试验结果对应的等高条形图.下列说法正确的是( )
A.服用A药物患病比例高于未服药物的患病比例
B.服用A药物对预防该疾病没有效果
C.在对B药物的试验中,患病小动物约占总数的55%
D.对该疾病的预防作用B药物比A药物更有效
12.2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.2月10日至2月14日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值
13.为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“?”表示服药者,“+”表示未服药者.
下列说法中,错误的是( )
A.服药组的指标x的均值和方差比未服药组的都低
B.未服药组的指标y的均值和方差比服药组的都高
C.以统计的频率作为概率,患者服药一段时间后指标x低于100的概率约为0.94
D.这种疾病的患者的生理指标y基本都大于1.5
二、解答题(共 35 分)
14.秉持“绿水青山就是金山银山”的生态文明发展理念,为推动新能源汽车产业迅速发展,有必要调查研究新能源汽车市场的生产与销售.下图是我国某地区2016年至2019年新能源汽车的销量(单位:万台)按季度(一年四个季度)统计制成的频率分布直方图.
(1)求直方图中a的值,并估计销量的中位数;
(2)请根据频率分布直方图估计新能源汽车平均每个季度的销售量(同一组数据用该组中间值代表),并以此预计2020年的销售量.
15.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生.
(2)在图(1)中将B对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
【答案】(1) 200名(2)见解析 (3) 150名
16.某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),?[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求a,众数,中位数.
(2)估计该校高二年级学生期中考试政治成绩的平均分.
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在[70?,?90)分数段抽取的人数是多少?
1188720012331700《作业推荐》—9.2用样本估计总体之抽样的数字特征的计算练习
一、单选题(共 65 分)
1.某老师从星期一到星期五收到的信件数分别为10,6,8, 5, 6,则该组数据的方差s2的值为( )
A.455 B.45 C.165 D.16
【答案】C
【解析】
【分析】
先求出某老师从星期一到星期五收到信件的平均数,由此能求出该组数据的方差.
【详解】
某老师从星期一到星期五收到信件的平均数为:1510+6+8+5+6=7,
∴该组数据的方差S2=1510?72++6?72+8?72+5?72+6?72=165,
故选:C.
【点睛】
本题主要考查一组数据的方差的求法,属于基础题.
2.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )
A.0.5 B.0.6 C.0.7 D.0.8
【答案】C
【解析】
【分析】
根据题先求出阅读过西游记的人数,进而得解.
【详解】
由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C.
【点睛】
本题考查容斥原理,渗透了数据处理和数学运算素养.采取去重法,利用转化与化归思想解题.
3.已知一组数据x1、x2、x3、x4、x5的平均数是2,方差是13,那么另一组数3x1?2、3x2?2、3x3?2、3x4?2、3x5?2的平均数,方差分别是( )
A.2,13 B.2,1 C.4,3 D.4,23
【答案】C
【解析】
【分析】
利用平均数和方差公式可得出结果.
【详解】
由题意可得x1+x2+x3+x4+x55=2,
x1?22+x2?22+x3?22+x4?22+x5?225=13,
则新数据的平均数为x=3x1?2+3x2?2+3x3?2+3x4?2+3x5?25 =3x1+x2+x3+x4+x55?2=3×2?2=4,
方差为s2=3x1?2?42+3x2?2?42+3x3?2?42+3x4?2?42+3x5?2?425 =9x1?22+x2?22+x3?22+x4?22+x5?225=9×13=3.
故选:C.
【点睛】
本题考查平均数与方差的计算,熟练利用公式是解答的关键,考查计算能力,属于基础题.
4.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
【答案】B
【解析】
评估这种农作物亩产量稳定程度的指标是标准差或方差,故选B.
点睛:众数:一组数据出现次数最多的数叫众数,众数反映一组数据的多数水平;
中位数:一组数据中间的数(起到分水岭的作用),中位数反映一组数据的中间水平;
平均数:反映一组数据的平均水平;
方差:反映一组数据偏离平均数的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
标准差是方差的算术平方根,意义在于反映一组数据的离散程度.
5.某校高一学生进行测试,随机抽取20名学生的测试成绩,绘制茎叶图如图所示,则这组数据的中位数和众数分别为( )
A.86,77 B.86,78 C.77,77 D.78,86
【答案】D
【解析】
【分析】
将数据由小到大排列,由此能求出这组数据的众数,中位数.
【详解】
由茎叶图知:数据为52、55、64、66、68、72、75、76、77、77、79、84、85、86、86、86、91、92、94、96,
因此,这组数据的众数为86,中位数为77+792=78.
故选:D.
【点睛】
本小题主要考查茎叶图、众数、中位数基础知识,属于基础题.
6.在某次赛车中,50名参赛选手的成绩(单位:min)全部介于13到18之间(包括13和18),将比赛成绩分为五组:第一组[13,14),第二组[14,15),··· ,第五组[17,18],其频率分布直方图如图所示.若成绩在[13,15)内的选手可获奖,则这50名选手中获奖的人数为( )
A.11 B.15 C.35 D.39
【答案】A
【解析】
【分析】
先根据频率分布直方图确定成绩在13,15内的频率,进而可求出结果.
【详解】
由题意可得:成绩在13,15内的频率为1?0.08?0.32?0.38=0.22,
又本次赛车中,共50名参赛选手,
所以,这50名选手中获奖的人数为50×0.22=11.
故选A
【点睛】
本题主要考查频率分布直方图,会根据频率分布直方图求频率即可,属于常考题型.
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
【答案】A
【解析】
【分析】
首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】
设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的30%+28%=58%>50%,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
8.如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
①深圳的变化幅度最小,北京的平均价格最高;
②深圳和度厦门往返机票的平均价格同去年相比有所下降;
③平均价格从高到低位于前三位的城市为北京,深圳,广州;
④平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【答案】C
【解析】
【分析】
根据图表逐项判定即可
【详解】
变化幅度看折线图,越接近零轴者变化幅度越小,位于零轴下方者表明价格下跌;平均价格看条形图,条形图越高平均价格越高,所以结论①②③都正确,结论④错误.
故选C.
【点睛】
本题考查折线图和条形图,准确理解题意是关键,是基础题
9.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
【答案】C
【解析】
【分析】
根据所给的六大素养雷达图逐个分析即可.
【详解】
A选项,甲的数据分析素养为5分, 乙的数据分析素养为4分, 乙的数据分析素养低于甲,选项错误;
B选项,乙的数学建模素养为3分, 乙的数学抽象为素养3分,选项错误;
C选项, 甲的六大素养指标值分别为5,4,5,4,5,4;乙的六大素养指标值分别为4,3,4,3,3,5,甲的六大素养指标值波动性比乙小,选项正确;
D选项,由C可知,甲的六大素养中,数学抽象,数学建模和数学运算最差,直观想象最最好,选项错误;
故选C.
【点睛】
本题考查了命题真假的判断以及统计图雷达图的识别和应用,考查学生简单的推理,属于基础题.
10.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
【答案】A
【解析】
【分析】
观察折线图可知月接待游客量每年7,8月份明显高于12月份,且折线图呈现增长趋势,高峰都出现在7、8月份,1月至6月的月接待游客量相对于7月至12月波动性更小.
【详解】
对于选项A,由图易知月接待游客量每年7,8月份明显高于12月份,故A错;
对于选项B,观察折线图的变化趋势可知年接待游客量逐年增加,故B正确;
对于选项C,D,由图可知显然正确.故选A.
【点睛】
本题考查折线图,考查考生的识图能力,属于基础题.
11.为了考察A、B两种药物预防某种疾病的效果,某研究所进行动物试验,已知参与两种药物试验的服药和未服药的动物数量相同,图1是A药试验结果对应的等高条形图;图2是B药试验结果对应的等高条形图.下列说法正确的是( )
A.服用A药物患病比例高于未服药物的患病比例
B.服用A药物对预防该疾病没有效果
C.在对B药物的试验中,患病小动物约占总数的55%
D.对该疾病的预防作用B药物比A药物更有效
【答案】D
【解析】
【分析】
根据两个表中的等高条形图,可得药物A的预防效果优于药物B的预防效果,即可求解.
【详解】
根据两个表中的等高条形图,可得:
服用A药物患病比例低于未服药物的患病比例,所以A不正确;
服用A药物对预防该疾病有一定效果,所以B不正确;
在对B药物的试验中,患病小动物小于总数的55% ,所以C不正确;
药物B实验显示不服药与服药的患病的差异较药物A实验显示明显大,该疾病的预防作用B药物比A药物更有效,所以D正确.
故选:D.
【点睛】
本题主要考查了等高条形图的应用问题,属于基础题.
12.2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.2月10日至2月14日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值
【答案】D
【解析】
【分析】
根据新增确诊曲线的走势可判断A选项的正误;根据新增确诊曲线与新增治愈曲线的位置关系可判断B选项的正误;根据2月10日至2月14日新增确诊曲线的走势可判断C选项的正误;根据新增确诊人数的变化可判断D选项的正误.综合可得出结论.
【详解】
对于A选项,由图象可知,2月下旬新增确诊人数呈波动下降趋势,A选项正确;
对于B选项,由图象可知,随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数,B选项正确;
对于C选项,由图象可知,2月10日至2月14日新增确诊人数波动最大,C选项正确;
对于D选项,在2月16日及以前,我国新型冠状病毒肺炎新增确诊人数大于新增治愈人数,我国新型冠状病毒肺炎累计确诊人数不在2月12日左右达到峰值,D选项错误.
故选:D.
【点睛】
本题考查统计图表的应用,考查数据处理能力,属于基础题.
13.为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“?”表示服药者,“+”表示未服药者.
下列说法中,错误的是( )
A.服药组的指标x的均值和方差比未服药组的都低
B.未服药组的指标y的均值和方差比服药组的都高
C.以统计的频率作为概率,患者服药一段时间后指标x低于100的概率约为0.94
D.这种疾病的患者的生理指标y基本都大于1.5
【答案】B
【解析】
【分析】
根据服药组和未服药组的数据分布可判断A、B选项的正误;观察服药组的指标x大于100的数据个数,可判断C选项的正误;观察未服药组生理指标y值的分布,可判断D选项的正误.综合可得出结论.
【详解】
对于A选项,服药组的指标x的取值相对集中,方差较小,且服药组的指标y的均值小于100,未服药组的指标y的均值大于100,A选项正确;
对于B选项,未服药组的指标y的取值相对集中,方差较小,B选项错误;
对于C选项,服药组的指标x值有3个大于100,所以患者服药一段时间后指标x低于100的概率约为0.94,C选项正确;
对于D选项,未服药组的指标y值只有1个数据比1.5小,则这种疾病的患者的生理指标y基本都大于1.5,D选项正确.
故选:B.
【点睛】
本题考查统计图表的应用,考查推理能力,属于基础题.
二、解答题(共 35 分)
14.秉持“绿水青山就是金山银山”的生态文明发展理念,为推动新能源汽车产业迅速发展,有必要调查研究新能源汽车市场的生产与销售.下图是我国某地区2016年至2019年新能源汽车的销量(单位:万台)按季度(一年四个季度)统计制成的频率分布直方图.
(1)求直方图中a的值,并估计销量的中位数;
(2)请根据频率分布直方图估计新能源汽车平均每个季度的销售量(同一组数据用该组中间值代表),并以此预计2020年的销售量.
【答案】(1)a=0.1125,中位数为16;(2)新能源汽车平均每个季度的销售量为17万台,以此预计2020年的销售量约为17万台.
【解析】
【分析】
(1)根据频率分布直方图中所有矩形面积之和为1可计算出a的值,利用中位数左边的矩形面积之和为0.5可求得销量的中位数的值;
(2)利用每个矩形底边的中点值乘以相应矩形的面积,相加可得出销量的平均数,由此可预计2020年的销售量.
【详解】
(1)由于频率分布直方图的所有矩形面积之和为1,
则0.0125+a+0.075+0.025×2×4=1,解得a=0.1125,
由于0.0125+0.1125×4=0.5,因此,销量的中位数为16;
(2)由频率分布直方图可知,新能源汽车平均每个季度的销售量为10×0.05+14×0.45+18×0.3+22×0.1+26×0.1=17(万台),
由此预测2020年的销售量为17万台.
【点睛】
本题考查利用频率分布直方图求参数、中位数以及平均数的计算,考查计算能力,属于基础题.
15.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生.
(2)在图(1)中将B对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
【答案】(1) 200名(2)见解析 (3) 150名
【解析】
【分析】
(1)从题图中知,选A的共60人,占总人数的百分比为30%,由此能求出本次一共调查了200名学生.
(2)被调查的学生中,求出选B的有100人,由此能补充完整的条形统计图.
(3)3000×5%=150,由雌能估计全校有150名学生平均每天参加体育活动的时间在0.5时以下.
【详解】
解:(1)从题图中知,选A的共60人,占总人数的百分比为30%,所以总人数为60÷30%=200,即本次一共调查了200名学生.
(2)被调查的学生中,选B的有200?60?30?10=100(人),补充完整的条形统计图如图所示.
(3)3000×5%=150,估计全校有150名学生平均每天参加体育活动的时间在0.5时以下.
【点睛】
本题考查频率分布直方图的应用,考查频率分布直方图的性质等基础知识,考查运算求解能力,是基础题.
16.某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),?[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求a,众数,中位数.
(2)估计该校高二年级学生期中考试政治成绩的平均分.
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在[70?,?90)分数段抽取的人数是多少?
【答案】(1)a=0.03众数为75中位数为2203;(2)平均分为71、(3)11.
【解析】
【分析】
(1)先根据频率之和为1,可求出a;再由频率最大的一组,得到众数;根据中位数两边的频率之和相等,可求出中位数;
(2)由每组的中间值乘以该组的频率,再求和,即可得出平均值;
(3)先由题意确定抽样比,进而可求出在[70?,?90)分数段抽取的人数.
【详解】
解析(1)由题意可得,(0.01+0.015×2+a+0.025+0.005)×10=1,解得a=0.03;
根据频率分布直方图可知:[70?,?80)分数段的频率最高,因此众数为75;
又由频率分布直方图可知:[40?,?70)分数段的频率为0.1+0.15+0.15=0.4,因为[70?,?80)分数段的频率为0.3,所以,中位数为70+13×10=2203.
(2)由题中数据可得:
该校高二年级学生政治成绩的平均分估计为:
(45×0.01+55×0.015+65×0.015+75×0.03+85×0.025+95×0.005)×10=71;
(3)因为总体共60名学生,样本容量为20,因此抽样比为2060=13;
又在[70?,?90)分数段共有60×(0.3+0.25)=33人,
因此,在[70?,?90)分数段抽取的人数是33×13=11人.
【点睛】
本题主要考查由频率分布直方图求中位数、众数、平均数、以及分层抽样的问题,熟记相关概念与公式即可,属于常考题型.
一、单选题(共 65 分)
1.某老师从星期一到星期五收到的信件数分别为10,6,8, 5, 6,则该组数据的方差s2的值为( )
A.455 B.45 C.165 D.16
2.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )
A.0.5 B.0.6 C.0.7 D.0.8
3.已知一组数据x1、x2、x3、x4、x5的平均数是2,方差是13,那么另一组数3x1?2、3x2?2、3x3?2、3x4?2、3x5?2的平均数,方差分别是( )
A.2,13 B.2,1 C.4,3 D.4,23
4.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
5.某校高一学生进行测试,随机抽取20名学生的测试成绩,绘制茎叶图如图所示,则这组数据的中位数和众数分别为( )
A.86,77 B.86,78 C.77,77 D.78,86
6.在某次赛车中,50名参赛选手的成绩(单位:min)全部介于13到18之间(包括13和18),将比赛成绩分为五组:第一组[13,14),第二组[14,15),··· ,第五组[17,18],其频率分布直方图如图所示.若成绩在[13,15)内的选手可获奖,则这50名选手中获奖的人数为( )
A.11 B.15 C.35 D.39
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
8.如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
①深圳的变化幅度最小,北京的平均价格最高;
②深圳和度厦门往返机票的平均价格同去年相比有所下降;
③平均价格从高到低位于前三位的城市为北京,深圳,广州;
④平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
10.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
11.为了考察A、B两种药物预防某种疾病的效果,某研究所进行动物试验,已知参与两种药物试验的服药和未服药的动物数量相同,图1是A药试验结果对应的等高条形图;图2是B药试验结果对应的等高条形图.下列说法正确的是( )
A.服用A药物患病比例高于未服药物的患病比例
B.服用A药物对预防该疾病没有效果
C.在对B药物的试验中,患病小动物约占总数的55%
D.对该疾病的预防作用B药物比A药物更有效
12.2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.2月10日至2月14日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值
13.为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“?”表示服药者,“+”表示未服药者.
下列说法中,错误的是( )
A.服药组的指标x的均值和方差比未服药组的都低
B.未服药组的指标y的均值和方差比服药组的都高
C.以统计的频率作为概率,患者服药一段时间后指标x低于100的概率约为0.94
D.这种疾病的患者的生理指标y基本都大于1.5
二、解答题(共 35 分)
14.秉持“绿水青山就是金山银山”的生态文明发展理念,为推动新能源汽车产业迅速发展,有必要调查研究新能源汽车市场的生产与销售.下图是我国某地区2016年至2019年新能源汽车的销量(单位:万台)按季度(一年四个季度)统计制成的频率分布直方图.
(1)求直方图中a的值,并估计销量的中位数;
(2)请根据频率分布直方图估计新能源汽车平均每个季度的销售量(同一组数据用该组中间值代表),并以此预计2020年的销售量.
15.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生.
(2)在图(1)中将B对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
【答案】(1) 200名(2)见解析 (3) 150名
16.某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),?[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求a,众数,中位数.
(2)估计该校高二年级学生期中考试政治成绩的平均分.
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在[70?,?90)分数段抽取的人数是多少?
1188720012331700《作业推荐》—9.2用样本估计总体之抽样的数字特征的计算练习
一、单选题(共 65 分)
1.某老师从星期一到星期五收到的信件数分别为10,6,8, 5, 6,则该组数据的方差s2的值为( )
A.455 B.45 C.165 D.16
【答案】C
【解析】
【分析】
先求出某老师从星期一到星期五收到信件的平均数,由此能求出该组数据的方差.
【详解】
某老师从星期一到星期五收到信件的平均数为:1510+6+8+5+6=7,
∴该组数据的方差S2=1510?72++6?72+8?72+5?72+6?72=165,
故选:C.
【点睛】
本题主要考查一组数据的方差的求法,属于基础题.
2.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )
A.0.5 B.0.6 C.0.7 D.0.8
【答案】C
【解析】
【分析】
根据题先求出阅读过西游记的人数,进而得解.
【详解】
由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C.
【点睛】
本题考查容斥原理,渗透了数据处理和数学运算素养.采取去重法,利用转化与化归思想解题.
3.已知一组数据x1、x2、x3、x4、x5的平均数是2,方差是13,那么另一组数3x1?2、3x2?2、3x3?2、3x4?2、3x5?2的平均数,方差分别是( )
A.2,13 B.2,1 C.4,3 D.4,23
【答案】C
【解析】
【分析】
利用平均数和方差公式可得出结果.
【详解】
由题意可得x1+x2+x3+x4+x55=2,
x1?22+x2?22+x3?22+x4?22+x5?225=13,
则新数据的平均数为x=3x1?2+3x2?2+3x3?2+3x4?2+3x5?25 =3x1+x2+x3+x4+x55?2=3×2?2=4,
方差为s2=3x1?2?42+3x2?2?42+3x3?2?42+3x4?2?42+3x5?2?425 =9x1?22+x2?22+x3?22+x4?22+x5?225=9×13=3.
故选:C.
【点睛】
本题考查平均数与方差的计算,熟练利用公式是解答的关键,考查计算能力,属于基础题.
4.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.x1,x2,…,xn的平均数 B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值 D.x1,x2,…,xn的中位数
【答案】B
【解析】
评估这种农作物亩产量稳定程度的指标是标准差或方差,故选B.
点睛:众数:一组数据出现次数最多的数叫众数,众数反映一组数据的多数水平;
中位数:一组数据中间的数(起到分水岭的作用),中位数反映一组数据的中间水平;
平均数:反映一组数据的平均水平;
方差:反映一组数据偏离平均数的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
标准差是方差的算术平方根,意义在于反映一组数据的离散程度.
5.某校高一学生进行测试,随机抽取20名学生的测试成绩,绘制茎叶图如图所示,则这组数据的中位数和众数分别为( )
A.86,77 B.86,78 C.77,77 D.78,86
【答案】D
【解析】
【分析】
将数据由小到大排列,由此能求出这组数据的众数,中位数.
【详解】
由茎叶图知:数据为52、55、64、66、68、72、75、76、77、77、79、84、85、86、86、86、91、92、94、96,
因此,这组数据的众数为86,中位数为77+792=78.
故选:D.
【点睛】
本小题主要考查茎叶图、众数、中位数基础知识,属于基础题.
6.在某次赛车中,50名参赛选手的成绩(单位:min)全部介于13到18之间(包括13和18),将比赛成绩分为五组:第一组[13,14),第二组[14,15),··· ,第五组[17,18],其频率分布直方图如图所示.若成绩在[13,15)内的选手可获奖,则这50名选手中获奖的人数为( )
A.11 B.15 C.35 D.39
【答案】A
【解析】
【分析】
先根据频率分布直方图确定成绩在13,15内的频率,进而可求出结果.
【详解】
由题意可得:成绩在13,15内的频率为1?0.08?0.32?0.38=0.22,
又本次赛车中,共50名参赛选手,
所以,这50名选手中获奖的人数为50×0.22=11.
故选A
【点睛】
本题主要考查频率分布直方图,会根据频率分布直方图求频率即可,属于常考题型.
7.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
【答案】A
【解析】
【分析】
首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】
设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的30%+28%=58%>50%,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
8.如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
①深圳的变化幅度最小,北京的平均价格最高;
②深圳和度厦门往返机票的平均价格同去年相比有所下降;
③平均价格从高到低位于前三位的城市为北京,深圳,广州;
④平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【答案】C
【解析】
【分析】
根据图表逐项判定即可
【详解】
变化幅度看折线图,越接近零轴者变化幅度越小,位于零轴下方者表明价格下跌;平均价格看条形图,条形图越高平均价格越高,所以结论①②③都正确,结论④错误.
故选C.
【点睛】
本题考查折线图和条形图,准确理解题意是关键,是基础题
9.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
【答案】C
【解析】
【分析】
根据所给的六大素养雷达图逐个分析即可.
【详解】
A选项,甲的数据分析素养为5分, 乙的数据分析素养为4分, 乙的数据分析素养低于甲,选项错误;
B选项,乙的数学建模素养为3分, 乙的数学抽象为素养3分,选项错误;
C选项, 甲的六大素养指标值分别为5,4,5,4,5,4;乙的六大素养指标值分别为4,3,4,3,3,5,甲的六大素养指标值波动性比乙小,选项正确;
D选项,由C可知,甲的六大素养中,数学抽象,数学建模和数学运算最差,直观想象最最好,选项错误;
故选C.
【点睛】
本题考查了命题真假的判断以及统计图雷达图的识别和应用,考查学生简单的推理,属于基础题.
10.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
【答案】A
【解析】
【分析】
观察折线图可知月接待游客量每年7,8月份明显高于12月份,且折线图呈现增长趋势,高峰都出现在7、8月份,1月至6月的月接待游客量相对于7月至12月波动性更小.
【详解】
对于选项A,由图易知月接待游客量每年7,8月份明显高于12月份,故A错;
对于选项B,观察折线图的变化趋势可知年接待游客量逐年增加,故B正确;
对于选项C,D,由图可知显然正确.故选A.
【点睛】
本题考查折线图,考查考生的识图能力,属于基础题.
11.为了考察A、B两种药物预防某种疾病的效果,某研究所进行动物试验,已知参与两种药物试验的服药和未服药的动物数量相同,图1是A药试验结果对应的等高条形图;图2是B药试验结果对应的等高条形图.下列说法正确的是( )
A.服用A药物患病比例高于未服药物的患病比例
B.服用A药物对预防该疾病没有效果
C.在对B药物的试验中,患病小动物约占总数的55%
D.对该疾病的预防作用B药物比A药物更有效
【答案】D
【解析】
【分析】
根据两个表中的等高条形图,可得药物A的预防效果优于药物B的预防效果,即可求解.
【详解】
根据两个表中的等高条形图,可得:
服用A药物患病比例低于未服药物的患病比例,所以A不正确;
服用A药物对预防该疾病有一定效果,所以B不正确;
在对B药物的试验中,患病小动物小于总数的55% ,所以C不正确;
药物B实验显示不服药与服药的患病的差异较药物A实验显示明显大,该疾病的预防作用B药物比A药物更有效,所以D正确.
故选:D.
【点睛】
本题主要考查了等高条形图的应用问题,属于基础题.
12.2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.2月10日至2月14日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值
【答案】D
【解析】
【分析】
根据新增确诊曲线的走势可判断A选项的正误;根据新增确诊曲线与新增治愈曲线的位置关系可判断B选项的正误;根据2月10日至2月14日新增确诊曲线的走势可判断C选项的正误;根据新增确诊人数的变化可判断D选项的正误.综合可得出结论.
【详解】
对于A选项,由图象可知,2月下旬新增确诊人数呈波动下降趋势,A选项正确;
对于B选项,由图象可知,随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数,B选项正确;
对于C选项,由图象可知,2月10日至2月14日新增确诊人数波动最大,C选项正确;
对于D选项,在2月16日及以前,我国新型冠状病毒肺炎新增确诊人数大于新增治愈人数,我国新型冠状病毒肺炎累计确诊人数不在2月12日左右达到峰值,D选项错误.
故选:D.
【点睛】
本题考查统计图表的应用,考查数据处理能力,属于基础题.
13.为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“?”表示服药者,“+”表示未服药者.
下列说法中,错误的是( )
A.服药组的指标x的均值和方差比未服药组的都低
B.未服药组的指标y的均值和方差比服药组的都高
C.以统计的频率作为概率,患者服药一段时间后指标x低于100的概率约为0.94
D.这种疾病的患者的生理指标y基本都大于1.5
【答案】B
【解析】
【分析】
根据服药组和未服药组的数据分布可判断A、B选项的正误;观察服药组的指标x大于100的数据个数,可判断C选项的正误;观察未服药组生理指标y值的分布,可判断D选项的正误.综合可得出结论.
【详解】
对于A选项,服药组的指标x的取值相对集中,方差较小,且服药组的指标y的均值小于100,未服药组的指标y的均值大于100,A选项正确;
对于B选项,未服药组的指标y的取值相对集中,方差较小,B选项错误;
对于C选项,服药组的指标x值有3个大于100,所以患者服药一段时间后指标x低于100的概率约为0.94,C选项正确;
对于D选项,未服药组的指标y值只有1个数据比1.5小,则这种疾病的患者的生理指标y基本都大于1.5,D选项正确.
故选:B.
【点睛】
本题考查统计图表的应用,考查推理能力,属于基础题.
二、解答题(共 35 分)
14.秉持“绿水青山就是金山银山”的生态文明发展理念,为推动新能源汽车产业迅速发展,有必要调查研究新能源汽车市场的生产与销售.下图是我国某地区2016年至2019年新能源汽车的销量(单位:万台)按季度(一年四个季度)统计制成的频率分布直方图.
(1)求直方图中a的值,并估计销量的中位数;
(2)请根据频率分布直方图估计新能源汽车平均每个季度的销售量(同一组数据用该组中间值代表),并以此预计2020年的销售量.
【答案】(1)a=0.1125,中位数为16;(2)新能源汽车平均每个季度的销售量为17万台,以此预计2020年的销售量约为17万台.
【解析】
【分析】
(1)根据频率分布直方图中所有矩形面积之和为1可计算出a的值,利用中位数左边的矩形面积之和为0.5可求得销量的中位数的值;
(2)利用每个矩形底边的中点值乘以相应矩形的面积,相加可得出销量的平均数,由此可预计2020年的销售量.
【详解】
(1)由于频率分布直方图的所有矩形面积之和为1,
则0.0125+a+0.075+0.025×2×4=1,解得a=0.1125,
由于0.0125+0.1125×4=0.5,因此,销量的中位数为16;
(2)由频率分布直方图可知,新能源汽车平均每个季度的销售量为10×0.05+14×0.45+18×0.3+22×0.1+26×0.1=17(万台),
由此预测2020年的销售量为17万台.
【点睛】
本题考查利用频率分布直方图求参数、中位数以及平均数的计算,考查计算能力,属于基础题.
15.为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生.
(2)在图(1)中将B对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
【答案】(1) 200名(2)见解析 (3) 150名
【解析】
【分析】
(1)从题图中知,选A的共60人,占总人数的百分比为30%,由此能求出本次一共调查了200名学生.
(2)被调查的学生中,求出选B的有100人,由此能补充完整的条形统计图.
(3)3000×5%=150,由雌能估计全校有150名学生平均每天参加体育活动的时间在0.5时以下.
【详解】
解:(1)从题图中知,选A的共60人,占总人数的百分比为30%,所以总人数为60÷30%=200,即本次一共调查了200名学生.
(2)被调查的学生中,选B的有200?60?30?10=100(人),补充完整的条形统计图如图所示.
(3)3000×5%=150,估计全校有150名学生平均每天参加体育活动的时间在0.5时以下.
【点睛】
本题考查频率分布直方图的应用,考查频率分布直方图的性质等基础知识,考查运算求解能力,是基础题.
16.某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),?[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求a,众数,中位数.
(2)估计该校高二年级学生期中考试政治成绩的平均分.
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在[70?,?90)分数段抽取的人数是多少?
【答案】(1)a=0.03众数为75中位数为2203;(2)平均分为71、(3)11.
【解析】
【分析】
(1)先根据频率之和为1,可求出a;再由频率最大的一组,得到众数;根据中位数两边的频率之和相等,可求出中位数;
(2)由每组的中间值乘以该组的频率,再求和,即可得出平均值;
(3)先由题意确定抽样比,进而可求出在[70?,?90)分数段抽取的人数.
【详解】
解析(1)由题意可得,(0.01+0.015×2+a+0.025+0.005)×10=1,解得a=0.03;
根据频率分布直方图可知:[70?,?80)分数段的频率最高,因此众数为75;
又由频率分布直方图可知:[40?,?70)分数段的频率为0.1+0.15+0.15=0.4,因为[70?,?80)分数段的频率为0.3,所以,中位数为70+13×10=2203.
(2)由题中数据可得:
该校高二年级学生政治成绩的平均分估计为:
(45×0.01+55×0.015+65×0.015+75×0.03+85×0.025+95×0.005)×10=71;
(3)因为总体共60名学生,样本容量为20,因此抽样比为2060=13;
又在[70?,?90)分数段共有60×(0.3+0.25)=33人,
因此,在[70?,?90)分数段抽取的人数是33×13=11人.
【点睛】
本题主要考查由频率分布直方图求中位数、众数、平均数、以及分层抽样的问题,熟记相关概念与公式即可,属于常考题型.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
