5.1.2 弧度制课件(共20张PPT)- 2020-2021学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 5.1.2 弧度制课件(共20张PPT)- 2020-2021学年高一上学期数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 917.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 20:27:31 | ||
图片预览




文档简介
5.1.2 弧度制
1.任意角
(正角、负角、零角)
2.角的运算
4.终边相同的角
5.区间角
3.象限角
相反角
知识回顾
{α|n·180°+30°≤α(2)1弧度的角:____________________________;
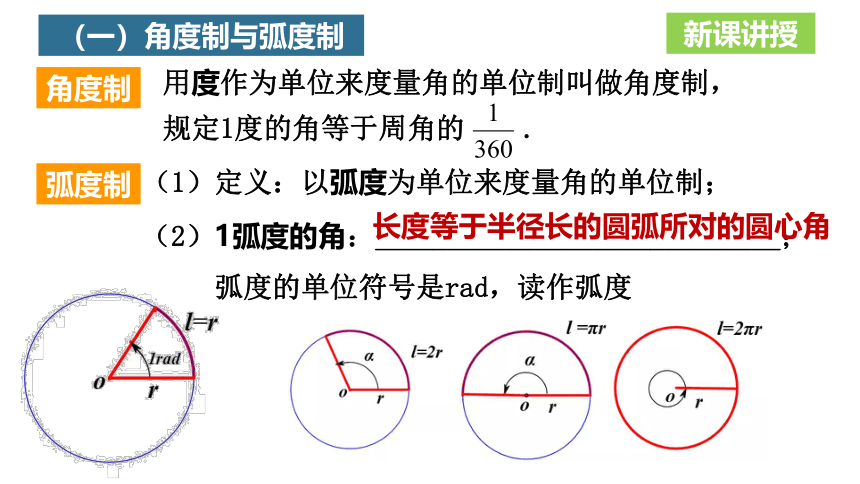
弧度的单位符号是rad,读作弧度
长度等于半径长的圆弧所对的圆心角
(一)角度制与弧度制
用度作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的 .
角度制
弧度制
(1)定义:以弧度为单位来度量角的单位制;
新课讲授
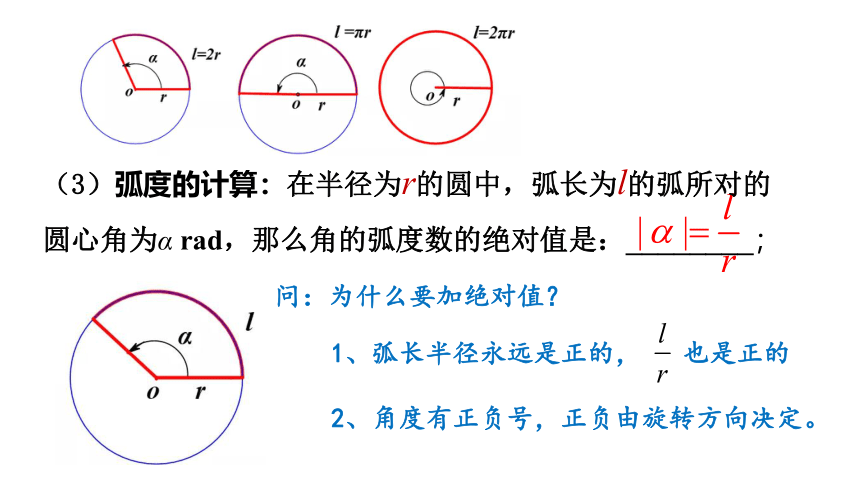
问:为什么要加绝对值?
1、弧长半径永远是正的, 也是正的
2、角度有正负号,正负由旋转方向决定。
(3)弧度的计算:在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么角的弧度数的绝对值是:________;
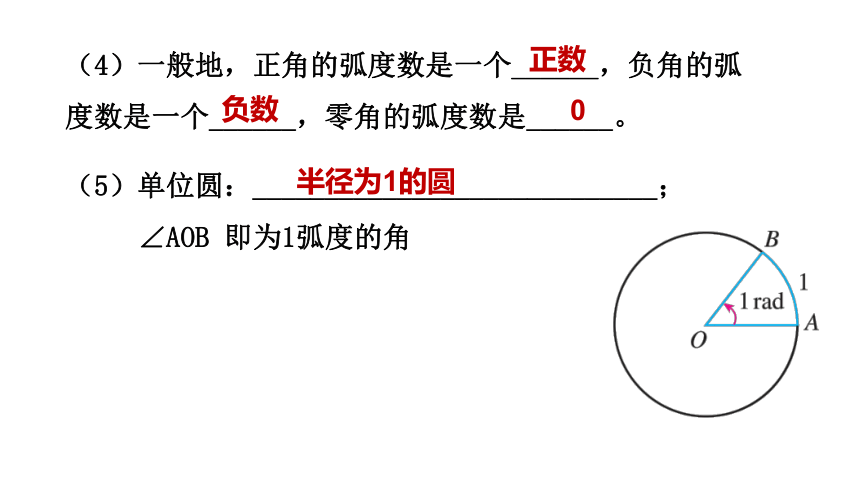
(4)一般地,正角的弧度数是一个______,负角的弧度数是一个______,零角的弧度数是______。
正数
负数
0
(5)单位圆:____________________________;
∠AOB 即为1弧度的角
半径为1的圆
弧度
即
≈0.01745 rad
圆心角为 的角所对弧长为 ,应为
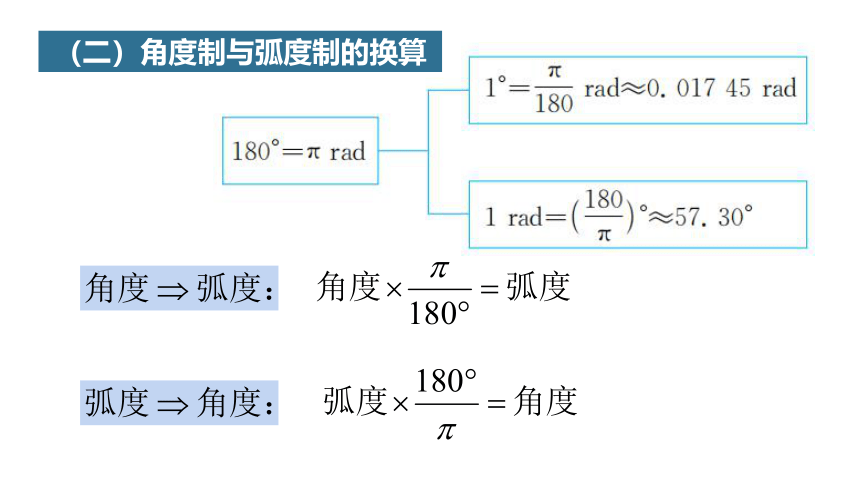
(二)角度制与弧度制的换算
新课讲授
(二)角度制与弧度制的换算
1.一般地,“弧度”与“rad“通常略去不写,而只写这个角所对应的弧度数.
2.角度制与弧度制互化时要抓住 弧度这个关键.
注意
例题1
把下列角度化成弧度.
例题2
把下列弧度化成角度.
有“分”“秒”,都先转换成“度”表示
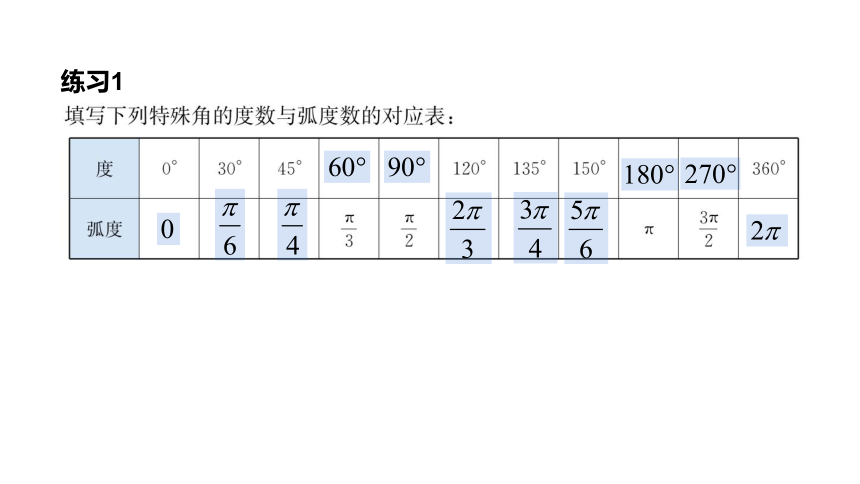
练习1
角的概念推广之后,无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系。
结论:弧度制实现了角和实数的转换.
角的集合与实数集合之间的对应关系
(1)每一个角都有唯一的一个实数与它对应;
(2)每一个实数也都有唯一的一个角与它对应。
正角
零角
负角
正实数
0
负实数
任意角的集合
实数集R
(1)用角度表示
(2)用弧度表示
与?终边相同的角可以表示为:
它们构成一个集合:
与?终边相同的角可以表示为:
它们构成一个集合:
例题3 终边相同的角的角度表示与弧度表示
若角 的终边经过点P(-1,-1),则用弧度表示角 的集合是
.
练习2
注意:角度制、弧度制二者不可混用
(三)扇形的弧长及面积公式
新课讲授
例题5
例题4
在半径为2的圆中,90°的圆心角所对的扇形的弧长是_________,面积是_________.
(1)分别用角度制、弧度制下的弧长公式,计算半径为1m的圆中,60o的圆心角所对的弧的长度.
(2)已知半径为120mm的圆上,有一条弧的长度是144mm,求该弧所对的圆心角的弧度数。
练习3
(3)若扇形的周长为30,当它的圆心角和半径各取什么值时,才能使扇形的面积最大?最大面积是多少?
1.角的度量有角度制和弧度制
2.角度和弧度的转换
3.弧度制下的弧长公式,面积公式
课堂小结
第一象限角:
第二象限角:
第三象限角:
第四象限角:
象限角的集合表示
终边与x轴负半轴重合的角
终边与y轴正半轴重合的角
终边与y轴负半轴重合的角
终边与x轴正半轴重合的角
终边与x轴重合的角
终边与y轴重合的角
轴线角的表示
终边相同的角的表示
若所求角β的终边落在某条射线上,则集合的形式为:
若所求角β的终边落在某条直线上,则集合的形式为:
若所求角β的终边落在某条互相垂直的两条线上,则集合的形式为:
课堂练习:
2.判断 的象限,并写出与它共终边的角的集合。
答案:
第三象限角
3. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
合( ) ?
扇形面积是
1.任意角
(正角、负角、零角)
2.角的运算
4.终边相同的角
5.区间角
3.象限角
相反角
知识回顾
{α|n·180°+30°≤α
弧度的单位符号是rad,读作弧度
长度等于半径长的圆弧所对的圆心角
(一)角度制与弧度制
用度作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的 .
角度制
弧度制
(1)定义:以弧度为单位来度量角的单位制;
新课讲授
问:为什么要加绝对值?
1、弧长半径永远是正的, 也是正的
2、角度有正负号,正负由旋转方向决定。
(3)弧度的计算:在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么角的弧度数的绝对值是:________;
(4)一般地,正角的弧度数是一个______,负角的弧度数是一个______,零角的弧度数是______。
正数
负数
0
(5)单位圆:____________________________;
∠AOB 即为1弧度的角
半径为1的圆
弧度
即
≈0.01745 rad
圆心角为 的角所对弧长为 ,应为
(二)角度制与弧度制的换算
新课讲授
(二)角度制与弧度制的换算
1.一般地,“弧度”与“rad“通常略去不写,而只写这个角所对应的弧度数.
2.角度制与弧度制互化时要抓住 弧度这个关键.
注意
例题1
把下列角度化成弧度.
例题2
把下列弧度化成角度.
有“分”“秒”,都先转换成“度”表示
练习1
角的概念推广之后,无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系。
结论:弧度制实现了角和实数的转换.
角的集合与实数集合之间的对应关系
(1)每一个角都有唯一的一个实数与它对应;
(2)每一个实数也都有唯一的一个角与它对应。
正角
零角
负角
正实数
0
负实数
任意角的集合
实数集R
(1)用角度表示
(2)用弧度表示
与?终边相同的角可以表示为:
它们构成一个集合:
与?终边相同的角可以表示为:
它们构成一个集合:
例题3 终边相同的角的角度表示与弧度表示
若角 的终边经过点P(-1,-1),则用弧度表示角 的集合是
.
练习2
注意:角度制、弧度制二者不可混用
(三)扇形的弧长及面积公式
新课讲授
例题5
例题4
在半径为2的圆中,90°的圆心角所对的扇形的弧长是_________,面积是_________.
(1)分别用角度制、弧度制下的弧长公式,计算半径为1m的圆中,60o的圆心角所对的弧的长度.
(2)已知半径为120mm的圆上,有一条弧的长度是144mm,求该弧所对的圆心角的弧度数。
练习3
(3)若扇形的周长为30,当它的圆心角和半径各取什么值时,才能使扇形的面积最大?最大面积是多少?
1.角的度量有角度制和弧度制
2.角度和弧度的转换
3.弧度制下的弧长公式,面积公式
课堂小结
第一象限角:
第二象限角:
第三象限角:
第四象限角:
象限角的集合表示
终边与x轴负半轴重合的角
终边与y轴正半轴重合的角
终边与y轴负半轴重合的角
终边与x轴正半轴重合的角
终边与x轴重合的角
终边与y轴重合的角
轴线角的表示
终边相同的角的表示
若所求角β的终边落在某条射线上,则集合的形式为:
若所求角β的终边落在某条直线上,则集合的形式为:
若所求角β的终边落在某条互相垂直的两条线上,则集合的形式为:
课堂练习:
2.判断 的象限,并写出与它共终边的角的集合。
答案:
第三象限角
3. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
合( ) ?
扇形面积是
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
