6.4.3 余弦定理、正弦定理(第3课时应用举例)(共13张PPT)课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 6.4.3 余弦定理、正弦定理(第3课时应用举例)(共13张PPT)课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 310.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 20:38:11 | ||
图片预览

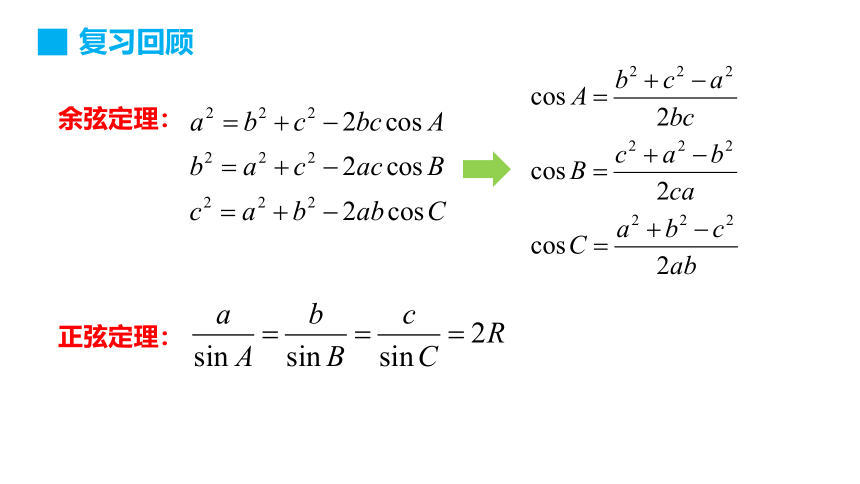



文档简介
20210322
正弦定理:
余弦定理:
复习回顾
(1)正弦定理的变形:
(2)三角形面积公式:
正弦定理:
边化角:
角化边:
在△ABC中,以下的三角关系式,在解答有关三角形问题时经常用到,要记熟并灵活地加以运用:
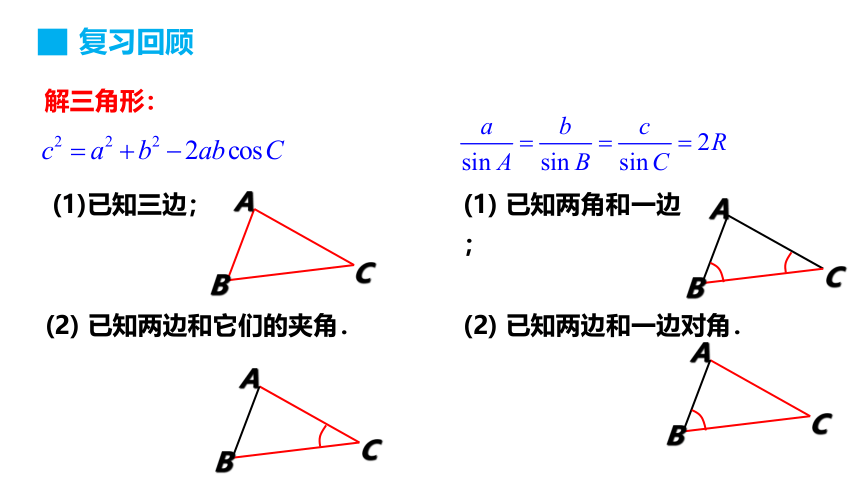
(1) 已知两角和一边;
(1)已知三边;
(2) 已知两边和一边对角.
(2) 已知两边和它们的夹角.
A
B
C
A
B
C
A
B
C
A
B
C
解三角形:
复习回顾
(1)基线的定义
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
(2)选择基线的原则
在测量过程中,为使测量工具有较高的精确度,应根据实际需要选取合适的基线长度,一般来说,基线_______,测量的精确度越高.
基线的概念与选择原则
越长
新课讲授
(1)仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线_______时叫仰角,目标视线在水平视线_______时叫俯角,如图所示.
相关术语
上方
下方
新课讲授
(2)方位角
指从___________顺时针转到目标方向线的水平角,如B点的方位角为α(如图所示).
正北方向
(3)方位角的其他表示——方向角
①正南方向:指从原点O出发的经过目标的射线与正南的方向线重合,即目标在正南的方向线上.依此可类推正北方向、正东方向和正西方向.
②东南方向:指经过目标的射线是正东和正南的夹角平分线(如图).
例2 如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点.设计一种测量建筑物高度AB的方法,并求出建筑物的高度.
解:选择一条水平基线HG,使H,G,B三点在同一条直线上,由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在 ACD中,根据正弦定理可得
B
E
A
H
G
D
C
h
a
求解三角形应用题的一般步骤:
(1)分析:理解题意,分清已知与未知,画出示意图;
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型;
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;
(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.
正弦定理:
余弦定理:
复习回顾
(1)正弦定理的变形:
(2)三角形面积公式:
正弦定理:
边化角:
角化边:
在△ABC中,以下的三角关系式,在解答有关三角形问题时经常用到,要记熟并灵活地加以运用:
(1) 已知两角和一边;
(1)已知三边;
(2) 已知两边和一边对角.
(2) 已知两边和它们的夹角.
A
B
C
A
B
C
A
B
C
A
B
C
解三角形:
复习回顾
(1)基线的定义
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
(2)选择基线的原则
在测量过程中,为使测量工具有较高的精确度,应根据实际需要选取合适的基线长度,一般来说,基线_______,测量的精确度越高.
基线的概念与选择原则
越长
新课讲授
(1)仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线_______时叫仰角,目标视线在水平视线_______时叫俯角,如图所示.
相关术语
上方
下方
新课讲授
(2)方位角
指从___________顺时针转到目标方向线的水平角,如B点的方位角为α(如图所示).
正北方向
(3)方位角的其他表示——方向角
①正南方向:指从原点O出发的经过目标的射线与正南的方向线重合,即目标在正南的方向线上.依此可类推正北方向、正东方向和正西方向.
②东南方向:指经过目标的射线是正东和正南的夹角平分线(如图).
例2 如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点.设计一种测量建筑物高度AB的方法,并求出建筑物的高度.
解:选择一条水平基线HG,使H,G,B三点在同一条直线上,由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在 ACD中,根据正弦定理可得
B
E
A
H
G
D
C
h
a
求解三角形应用题的一般步骤:
(1)分析:理解题意,分清已知与未知,画出示意图;
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型;
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;
(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
