6.4.3 余弦定理、正弦定理(第1课时)课件(共19张PPT)——2020-2021学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 6.4.3 余弦定理、正弦定理(第1课时)课件(共19张PPT)——2020-2021学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 338.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 20:35:57 | ||
图片预览




文档简介
——第一课时 余弦定理
20210317
A
B
C
a
b
c
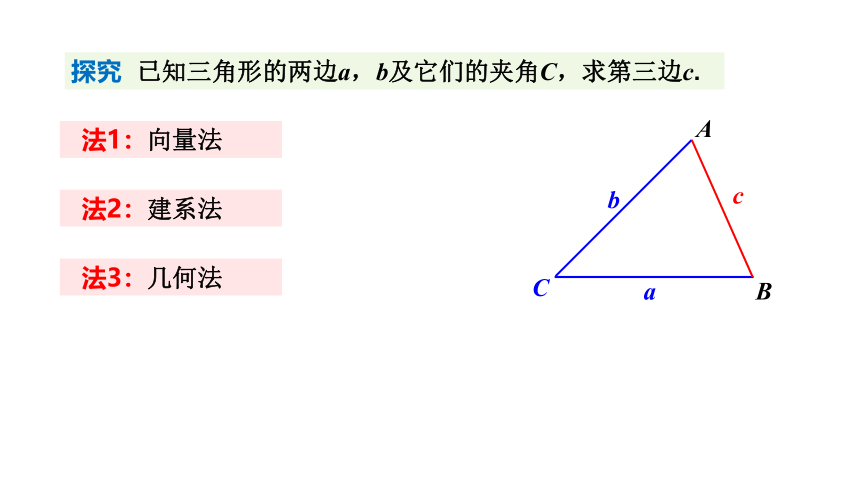
探究 已知三角形的两边a,b及它们的夹角C,求第三边c.
法1:向量法
法2:建系法
法3:几何法
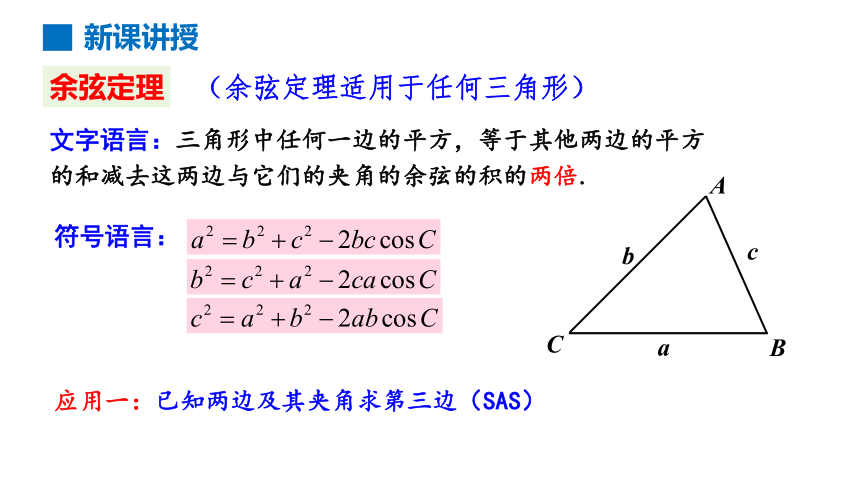
文字语言:三角形中任何一边的平方,等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
应用一:已知两边及其夹角求第三边(SAS)
新课讲授
余弦定理
符号语言:
A
B
C
a
b
c
(余弦定理适用于任何三角形)
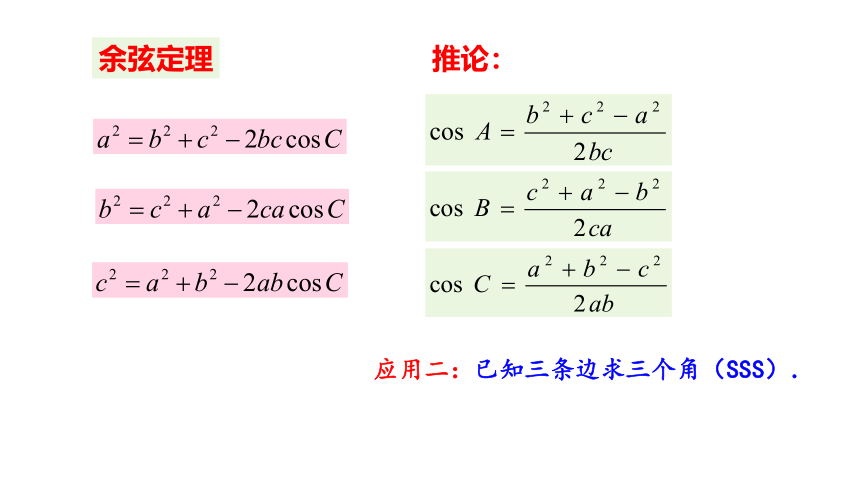
应用二:已知三条边求三个角(SSS).
余弦定理
推论:
问题1:勾股定理与余弦定理有何关系?
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
问题2:公式的结构特征怎样?
(1)轮换对称,简洁优美;
剖析定理
(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
例题1(1)已知b=8,c=3,A= 60°,求a.
a? = b?+c?-2bccosA
= 64+9-2×8×3cos 60° = 49,
a = 7.
应用一:已知两边及其夹角求第三边
一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的____. 已知三角形的几个元素求其他元素的过程叫做___________.
元素
解三角形
解三角形:
例题讲授
应用一:已知两边及其夹角求第三边
例题1(2)在△ABC中,已知a= ,c=2,B=150°,求b.
应用二:已知三条边求第三个角
例题2 在△ABC中,已知a=20,b=29,c=21,求B.
例题3 在△ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状.
应用三:判断三角形的形状
【归纳总结】一般地,判断△ABC是锐角三角形,直角三角形还是钝角三角形,可用如下方法.
设a是最长边,则
应用三:判断三角形的形状
A
B
C
a
b
c
练习:
(2)已知三边求三个角;
(1)已知两边和它们的夹角,求第三边和其他两个角.
归纳:余弦定理的应用
(3)判断三角形的形状,求三角形的面积
课堂小结
练习巩固
3. 在△ABC中,已知 ,求角C.
1.
2.
A
5. 设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.
4. 在△ABC中,A+C=2B,a=2,b+c=7,求b.
5. 设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.
6.
法1:向量法
A
B
C
a
b
c
A
B
C
a
b
c
x
y
法2:建系法
A
B
C
a
b
c
D
法3:几何法
20210317
A
B
C
a
b
c
探究 已知三角形的两边a,b及它们的夹角C,求第三边c.
法1:向量法
法2:建系法
法3:几何法
文字语言:三角形中任何一边的平方,等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
应用一:已知两边及其夹角求第三边(SAS)
新课讲授
余弦定理
符号语言:
A
B
C
a
b
c
(余弦定理适用于任何三角形)
应用二:已知三条边求三个角(SSS).
余弦定理
推论:
问题1:勾股定理与余弦定理有何关系?
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
问题2:公式的结构特征怎样?
(1)轮换对称,简洁优美;
剖析定理
(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
例题1(1)已知b=8,c=3,A= 60°,求a.
a? = b?+c?-2bccosA
= 64+9-2×8×3cos 60° = 49,
a = 7.
应用一:已知两边及其夹角求第三边
一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的____. 已知三角形的几个元素求其他元素的过程叫做___________.
元素
解三角形
解三角形:
例题讲授
应用一:已知两边及其夹角求第三边
例题1(2)在△ABC中,已知a= ,c=2,B=150°,求b.
应用二:已知三条边求第三个角
例题2 在△ABC中,已知a=20,b=29,c=21,求B.
例题3 在△ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状.
应用三:判断三角形的形状
【归纳总结】一般地,判断△ABC是锐角三角形,直角三角形还是钝角三角形,可用如下方法.
设a是最长边,则
应用三:判断三角形的形状
A
B
C
a
b
c
练习:
(2)已知三边求三个角;
(1)已知两边和它们的夹角,求第三边和其他两个角.
归纳:余弦定理的应用
(3)判断三角形的形状,求三角形的面积
课堂小结
练习巩固
3. 在△ABC中,已知 ,求角C.
1.
2.
A
5. 设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.
4. 在△ABC中,A+C=2B,a=2,b+c=7,求b.
5. 设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.
6.
法1:向量法
A
B
C
a
b
c
A
B
C
a
b
c
x
y
法2:建系法
A
B
C
a
b
c
D
法3:几何法
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
