第1章全等三角形 同步训练(附答案) 2021--2020学年苏科版八年级数学上册(word版含解析)
文档属性
| 名称 | 第1章全等三角形 同步训练(附答案) 2021--2020学年苏科版八年级数学上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 00:00:00 | ||
图片预览


文档简介
2021年苏科版八年级数学上册《第1章全等三角形》同步优生辅导训练(附答案)
1.在△ABC和△DEF中,∠A=∠D,AB=DE,则添加下列条件不能使△ABC≌△DEF成立的是( )
A.∠B=∠E B.∠C=∠F C.AC=DF D.BC=EF
2.如图,△ABC≌△ADE,若∠B=40°,∠E=30°,则∠DAE的度数为( )
A.70° B.110° C.120° D.130°
3.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以 B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了 D.带1、4或2、4或3、4去均可
4.如图,在△ABC和△DEF中,AC=DF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
A.∠A=∠D B.BE=CF
C.∠ACB=∠DFE=90° D.∠B=∠DEF
5.如图,B、C、D在同一直线上,∠B=∠D=90°,AB=CD=1,BC=DE=3,则△ACE的面积为 .
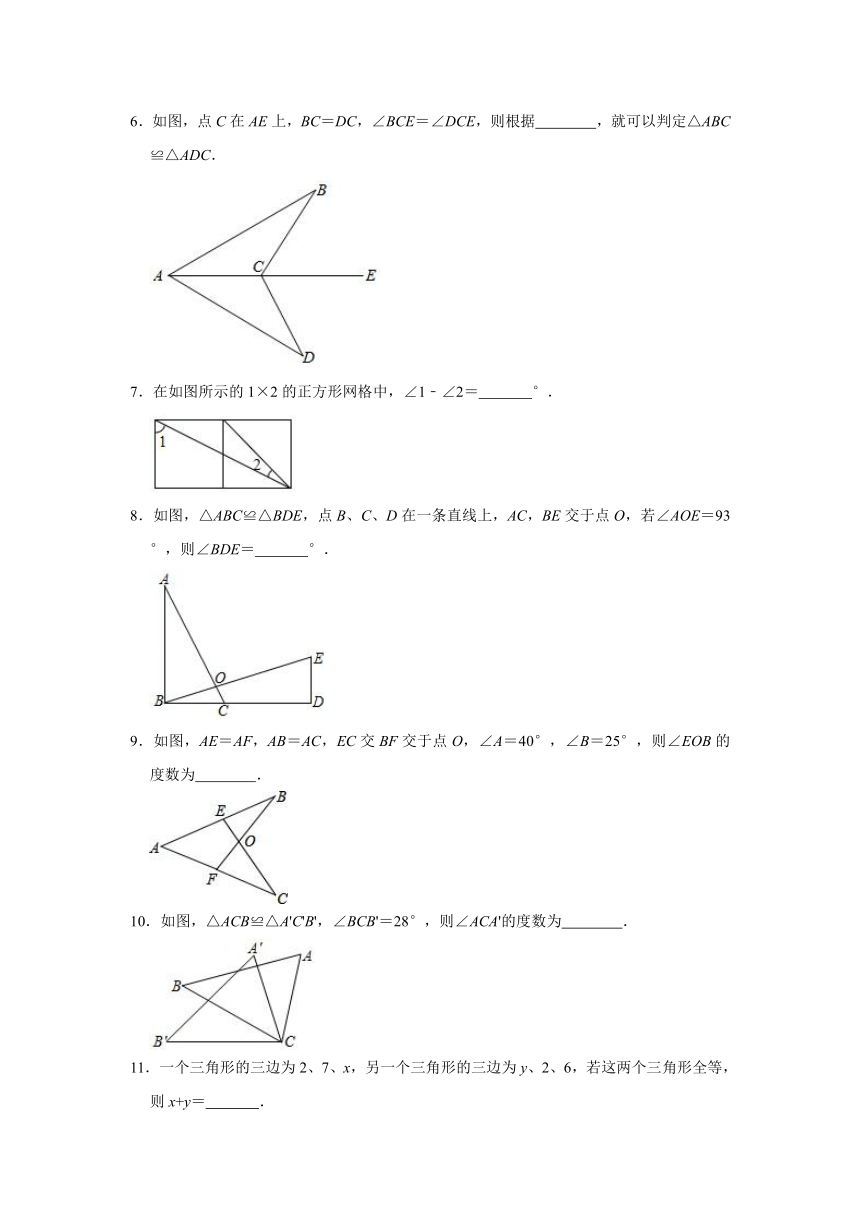
6.如图,点C在AE上,BC=DC,∠BCE=∠DCE,则根据 ,就可以判定△ABC≌△ADC.
7.在如图所示的1×2的正方形网格中,∠1﹣∠2= °.
8.如图,△ABC≌△BDE,点B、C、D在一条直线上,AC,BE交于点O,若∠AOE=93°,则∠BDE= °.
9.如图,AE=AF,AB=AC,EC交BF交于点O,∠A=40°,∠B=25°,则∠EOB的度数为 .
10.如图,△ACB≌△A'C'B',∠BCB'=28°,则∠ACA'的度数为 .
11.一个三角形的三边为2、7、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .
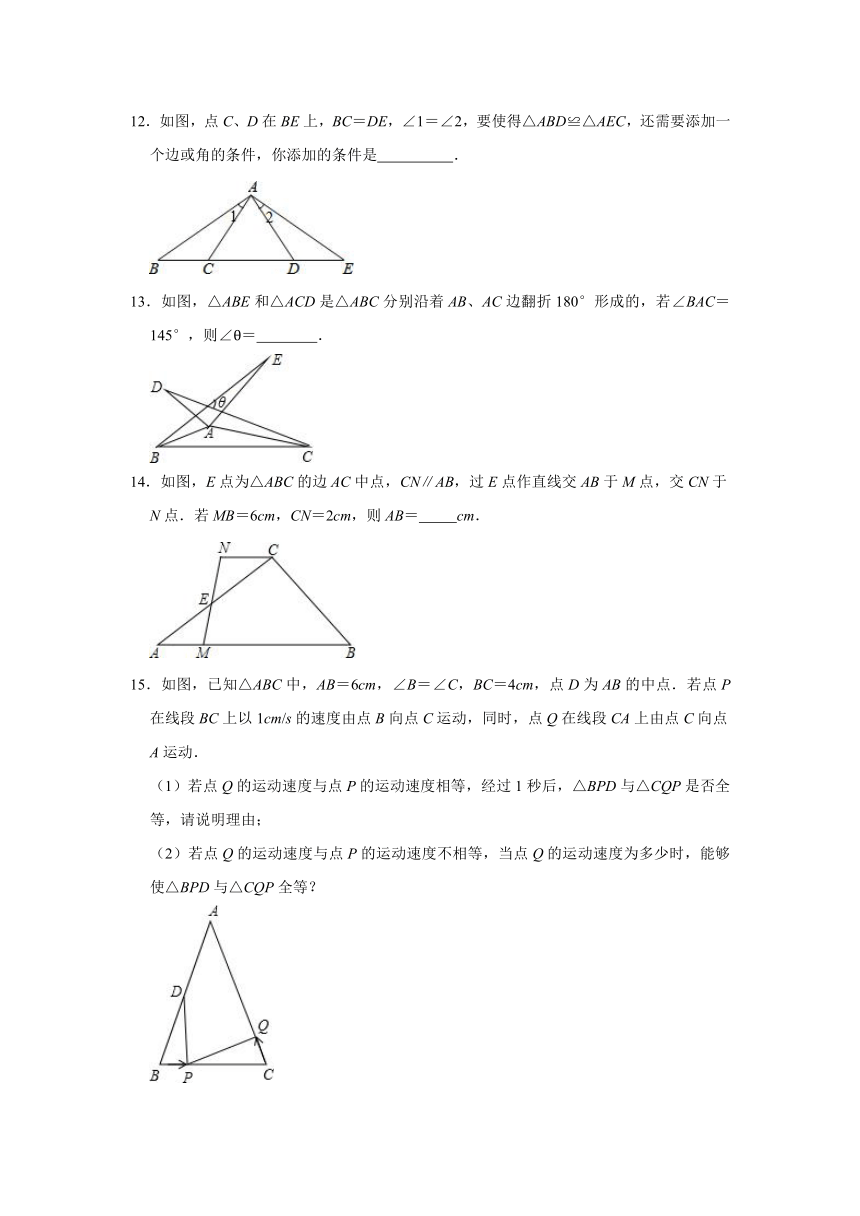
12.如图,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个边或角的条件,你添加的条件是 .
13.如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=145°,则∠θ= .
14.如图,E点为△ABC的边AC中点,CN∥AB,过E点作直线交AB于M点,交CN于N点.若MB=6cm,CN=2cm,则AB= cm.
15.如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
16.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:
(1)EC=BF;
(2)EC⊥BF.
17.如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:AC=AO+AP.
18.在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;
(2)动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PG⊥CD于点G,QF⊥CD于点F.问两动点运动多长时间时△OPG与△OQF全等?
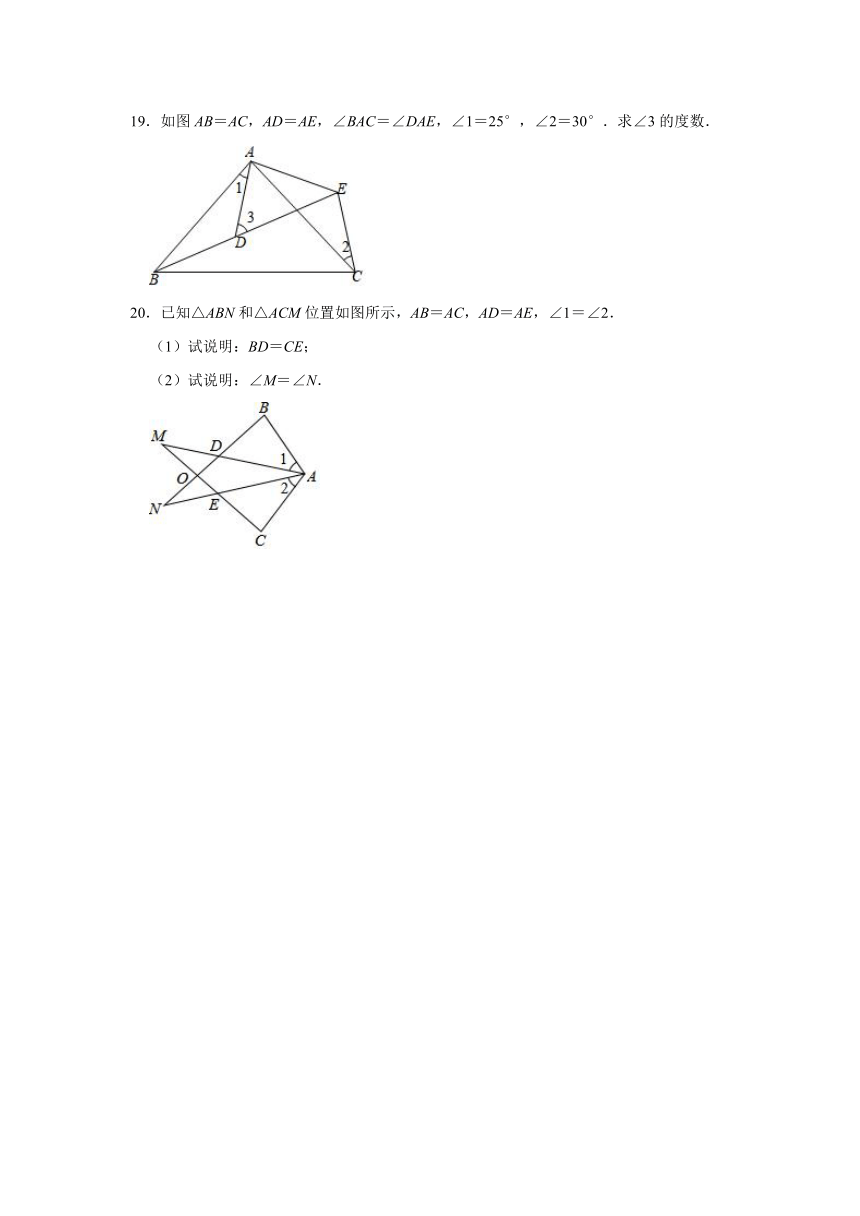
19.如图AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°.求∠3的度数.
20.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)试说明:BD=CE;
(2)试说明:∠M=∠N.
参考答案
1.解:A、添加∠B=∠E,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
B、添加∠C=∠F,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
C、添加AC=DF,可利用SAS定理判定△ABC≌△DEF,故此选项不合题意;
D、添加BC=EF,不能判定△ABC≌△DEF,故此选项符合题意;
故选:D.
2.解:∵△ABC≌△ADE,
∴∠B=∠D=40°,
∴∠DAE=180°﹣∠D﹣∠E=180°﹣40°﹣30°=110°.
故选:B.
3.解:带③、④可以用“角边角”确定三角形,
带①、④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形,
故选:D.
4.解:∵AC=DF,AB=DE,
∴添加∠A=∠D,可利用SAS证明△ABC≌△DEF,故A正确;
∴添加BE=CF,得出BC=EF,利用SSS证明△ABC≌△DEF,故B正确;
∴添加∠ACB=∠DFE=90°,利用HL证明Rt△ABC≌Rt△DEF,故C正确;
故选:D.
5.解:在△ABC和△CDE中,
,
∴△ABC≌△CDE(SAS),
∴AC=CE,∠ACB=∠CED,
∵∠CED+∠ECD=90°,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°,
∵∠B=90°,AB=1,BC=3,
∴S△ACE=××=5,
故答案为:5.
6.解:∵∠BCE=∠DCE,
∴∠ACB=∠ACD,
在△ABC与△ADC中,
,
∴△ABC≌△ADC(SAS).
故答案是:SAS.
7.解:在△ABD和△CDB中,
∴△ADB≌△CBD(SSS),
∴∠1=∠CBD,
∴∠1﹣∠2=∠CBD﹣∠2=∠CBE=45°,
故答案为:45.
8.解:∵△ABC≌△BDE,
∴∠A=∠EBD,∠ABC=∠BDE,
∵∠AOE=93°,
∴∠BDE=∠ABC=∠ABO+∠EBD
=∠ABO+∠A
=180°﹣∠AOB
=180°﹣(180°﹣93°)
=93°,
故答案为:93.
9.解:∵AE=AF,∠A=∠A,AB=AC,
∴△AEC≌△AFB(SAS)
∴∠B=∠C=25°,
∵∠OFC=∠A+∠B=65°,
∴∠FOC=180°﹣∠C﹣∠OFC=90°
故答案为:90°.
10.解:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∵∠BCB′=∠A′CB′﹣∠A′CB,
∴∠ACA′=∠ACB﹣∠A′CB,
∴∠ACA′=∠BCB′=28°.
故答案为:28°.
11.解:∵两个三角形全等,
∴x=6,y=7,
∴x+y=7+6=13.
故答案为:13
12.解:添加∠B=∠E;
∵BC=DE,
∴CB+CD=DE+CD,
即BD=CE,
∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠BAD=∠EAC,
在△ABD和△AEC中,
,
∴△ABD≌△AEC(AAS),
故答案为:∠B=∠E.
13.解:∵∠BAC=145°
∴∠ABC+∠ACB=35°
∵∠EBA=∠ABC,∠DCA=∠ACB
∴∠EBA+∠ABC+∠DCA+∠ACB=2(∠ABC+∠ACB)=70°,即∠EBC+∠DCB=70°
∴θ=70°.
故答案为:70°
14.解:∵CN∥AB,
∴∠NCE=∠MAE,
又∵E是AC中点,
∴AE=CE,
而∠AEM=∠CEN,
在△CNE和△AME中,
,
∴△CNE≌△AME,
∴AM=CN,
∴AB=AM+BM=CN+BM=2+6=8,
故答案为:8.
三.解答题(共6小题)
15.解:(1)全等,理由如下:
∵t=1秒,
∴BP=CQ=1×1=1厘米,
∵AB=6cm,点D为AB的中点,
∴BD=3cm.
又∵PC=BC﹣BP,BC=4cm,
∴PC=4﹣1=3cm,
∴PC=BD.
∵∠B=∠C,
∴△BPD≌△CPQ;
(2)∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
则BP=CP=2,BD=CQ=3,
∴点P,点Q运动的时间为:t=2秒,
∴vQ=1.5cm/s;
16.证明:(1)∵AE⊥AB,AF⊥AC,
∠EAB=∠FAC=90°,
∴∠EAC=∠BAF,
在△EAC和△BAF中,
,
∴△EAC≌△BAF,
∴EC=BF.
(2)设AC交BF于O.
∵△EAC≌△BAF,
∴∠AFO=∠OCM,∵∠AOF=∠MOC,
∴∠OMC=∠OAF=90°,
∴EC⊥BF.
17.解:(1)连接BO,如图1所示:
∵AB=AC,AD⊥BC,
∴BD=CD,∠ODB=∠ODC,
在△OBD和△OCD中,
,
∴△OBD≌△OCD(SAS),
∴OB=OC,
又∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
又∵∠BAC=120°,
∠ABC=∠ACB=30°,
又∵∠ABD=∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°;
(2)过点O作OH⊥BP于点H,如图2所示:
∵∠BAC=120°,AB=AC,AD⊥BC,
∴∠HAO=∠CAD=60°,
又∵OH⊥BP,
∴∠OHA=90°,
∴∠HOA=30°,
∴AO=2AH,
又∵BO=PO,OH⊥BP,
∴BH=PH,
又∵HP=AP+AH,
∴BH=AP+AH,
又∵AB=BH+AH,
∴AB=AP+2AH,
又∵AB=AC,AO=2AH,
∴AC=AP+AO.
18.解:(1)①如图,∵∠DBO=∠ABO,OB⊥AE,
∴∠BAO=∠BEO,
∴AB=BE,
∴AO=OE,
∵∠CAy=∠BAO,
∴∠CAy=∠BEO,
∴∠DEO=∠CAO
在△ACO与△EDO中,,
∴△ACO≌△EDO(ASA);
②由①知,△ACO≌△EDO,
∴∠C=∠D,AC=DE,
∴AC∥BD,AC=BD﹣10;
(2)设运动的时间为t秒,
(i)当点P、Q分别在y轴、x轴上时PO=QO得:6﹣t=8﹣2t,解得t=2(秒),
(ii)当点P、Q都在y轴上时PO=QO得:6﹣t=2t﹣8,解得t=(秒),
(iii)当点P在x轴上,Q在y轴时若二者都没有提前停止,则PO=QO得:t﹣6=2t﹣8,解得t=2(秒)不合题意;
当点Q提前停止时,有t﹣6=6,解得t=12(秒),
综上所述:当两动点运动时间为2、、12秒时,△OPE与△OQF全等
19.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠CAE.
在△ADB和△AEC中,
,
∴△ADB≌AEC(SAS),
∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD.
∴∠3=25°+30°=55°.
答:∠3的度数为55°.
20.(1)证明:在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)证明:∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM,
由(1)得:△ABD≌△ACE,
∴∠B=∠C,
在△ACM和△ABN中,,
∴△ACM≌△ABN(ASA),
∴∠M=∠N.
1.在△ABC和△DEF中,∠A=∠D,AB=DE,则添加下列条件不能使△ABC≌△DEF成立的是( )
A.∠B=∠E B.∠C=∠F C.AC=DF D.BC=EF
2.如图,△ABC≌△ADE,若∠B=40°,∠E=30°,则∠DAE的度数为( )
A.70° B.110° C.120° D.130°
3.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以 B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了 D.带1、4或2、4或3、4去均可
4.如图,在△ABC和△DEF中,AC=DF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
A.∠A=∠D B.BE=CF
C.∠ACB=∠DFE=90° D.∠B=∠DEF
5.如图,B、C、D在同一直线上,∠B=∠D=90°,AB=CD=1,BC=DE=3,则△ACE的面积为 .
6.如图,点C在AE上,BC=DC,∠BCE=∠DCE,则根据 ,就可以判定△ABC≌△ADC.
7.在如图所示的1×2的正方形网格中,∠1﹣∠2= °.
8.如图,△ABC≌△BDE,点B、C、D在一条直线上,AC,BE交于点O,若∠AOE=93°,则∠BDE= °.
9.如图,AE=AF,AB=AC,EC交BF交于点O,∠A=40°,∠B=25°,则∠EOB的度数为 .
10.如图,△ACB≌△A'C'B',∠BCB'=28°,则∠ACA'的度数为 .
11.一个三角形的三边为2、7、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .
12.如图,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个边或角的条件,你添加的条件是 .
13.如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=145°,则∠θ= .
14.如图,E点为△ABC的边AC中点,CN∥AB,过E点作直线交AB于M点,交CN于N点.若MB=6cm,CN=2cm,则AB= cm.
15.如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
16.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:
(1)EC=BF;
(2)EC⊥BF.
17.如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:AC=AO+AP.
18.在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;
(2)动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PG⊥CD于点G,QF⊥CD于点F.问两动点运动多长时间时△OPG与△OQF全等?
19.如图AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°.求∠3的度数.
20.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)试说明:BD=CE;
(2)试说明:∠M=∠N.
参考答案
1.解:A、添加∠B=∠E,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
B、添加∠C=∠F,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
C、添加AC=DF,可利用SAS定理判定△ABC≌△DEF,故此选项不合题意;
D、添加BC=EF,不能判定△ABC≌△DEF,故此选项符合题意;
故选:D.
2.解:∵△ABC≌△ADE,
∴∠B=∠D=40°,
∴∠DAE=180°﹣∠D﹣∠E=180°﹣40°﹣30°=110°.
故选:B.
3.解:带③、④可以用“角边角”确定三角形,
带①、④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形,
故选:D.
4.解:∵AC=DF,AB=DE,
∴添加∠A=∠D,可利用SAS证明△ABC≌△DEF,故A正确;
∴添加BE=CF,得出BC=EF,利用SSS证明△ABC≌△DEF,故B正确;
∴添加∠ACB=∠DFE=90°,利用HL证明Rt△ABC≌Rt△DEF,故C正确;
故选:D.
5.解:在△ABC和△CDE中,
,
∴△ABC≌△CDE(SAS),
∴AC=CE,∠ACB=∠CED,
∵∠CED+∠ECD=90°,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°,
∵∠B=90°,AB=1,BC=3,
∴S△ACE=××=5,
故答案为:5.
6.解:∵∠BCE=∠DCE,
∴∠ACB=∠ACD,
在△ABC与△ADC中,
,
∴△ABC≌△ADC(SAS).
故答案是:SAS.
7.解:在△ABD和△CDB中,
∴△ADB≌△CBD(SSS),
∴∠1=∠CBD,
∴∠1﹣∠2=∠CBD﹣∠2=∠CBE=45°,
故答案为:45.
8.解:∵△ABC≌△BDE,
∴∠A=∠EBD,∠ABC=∠BDE,
∵∠AOE=93°,
∴∠BDE=∠ABC=∠ABO+∠EBD
=∠ABO+∠A
=180°﹣∠AOB
=180°﹣(180°﹣93°)
=93°,
故答案为:93.
9.解:∵AE=AF,∠A=∠A,AB=AC,
∴△AEC≌△AFB(SAS)
∴∠B=∠C=25°,
∵∠OFC=∠A+∠B=65°,
∴∠FOC=180°﹣∠C﹣∠OFC=90°
故答案为:90°.
10.解:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∵∠BCB′=∠A′CB′﹣∠A′CB,
∴∠ACA′=∠ACB﹣∠A′CB,
∴∠ACA′=∠BCB′=28°.
故答案为:28°.
11.解:∵两个三角形全等,
∴x=6,y=7,
∴x+y=7+6=13.
故答案为:13
12.解:添加∠B=∠E;
∵BC=DE,
∴CB+CD=DE+CD,
即BD=CE,
∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠BAD=∠EAC,
在△ABD和△AEC中,
,
∴△ABD≌△AEC(AAS),
故答案为:∠B=∠E.
13.解:∵∠BAC=145°
∴∠ABC+∠ACB=35°
∵∠EBA=∠ABC,∠DCA=∠ACB
∴∠EBA+∠ABC+∠DCA+∠ACB=2(∠ABC+∠ACB)=70°,即∠EBC+∠DCB=70°
∴θ=70°.
故答案为:70°
14.解:∵CN∥AB,
∴∠NCE=∠MAE,
又∵E是AC中点,
∴AE=CE,
而∠AEM=∠CEN,
在△CNE和△AME中,
,
∴△CNE≌△AME,
∴AM=CN,
∴AB=AM+BM=CN+BM=2+6=8,
故答案为:8.
三.解答题(共6小题)
15.解:(1)全等,理由如下:
∵t=1秒,
∴BP=CQ=1×1=1厘米,
∵AB=6cm,点D为AB的中点,
∴BD=3cm.
又∵PC=BC﹣BP,BC=4cm,
∴PC=4﹣1=3cm,
∴PC=BD.
∵∠B=∠C,
∴△BPD≌△CPQ;
(2)∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
则BP=CP=2,BD=CQ=3,
∴点P,点Q运动的时间为:t=2秒,
∴vQ=1.5cm/s;
16.证明:(1)∵AE⊥AB,AF⊥AC,
∠EAB=∠FAC=90°,
∴∠EAC=∠BAF,
在△EAC和△BAF中,
,
∴△EAC≌△BAF,
∴EC=BF.
(2)设AC交BF于O.
∵△EAC≌△BAF,
∴∠AFO=∠OCM,∵∠AOF=∠MOC,
∴∠OMC=∠OAF=90°,
∴EC⊥BF.
17.解:(1)连接BO,如图1所示:
∵AB=AC,AD⊥BC,
∴BD=CD,∠ODB=∠ODC,
在△OBD和△OCD中,
,
∴△OBD≌△OCD(SAS),
∴OB=OC,
又∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
又∵∠BAC=120°,
∠ABC=∠ACB=30°,
又∵∠ABD=∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°;
(2)过点O作OH⊥BP于点H,如图2所示:
∵∠BAC=120°,AB=AC,AD⊥BC,
∴∠HAO=∠CAD=60°,
又∵OH⊥BP,
∴∠OHA=90°,
∴∠HOA=30°,
∴AO=2AH,
又∵BO=PO,OH⊥BP,
∴BH=PH,
又∵HP=AP+AH,
∴BH=AP+AH,
又∵AB=BH+AH,
∴AB=AP+2AH,
又∵AB=AC,AO=2AH,
∴AC=AP+AO.
18.解:(1)①如图,∵∠DBO=∠ABO,OB⊥AE,
∴∠BAO=∠BEO,
∴AB=BE,
∴AO=OE,
∵∠CAy=∠BAO,
∴∠CAy=∠BEO,
∴∠DEO=∠CAO
在△ACO与△EDO中,,
∴△ACO≌△EDO(ASA);
②由①知,△ACO≌△EDO,
∴∠C=∠D,AC=DE,
∴AC∥BD,AC=BD﹣10;
(2)设运动的时间为t秒,
(i)当点P、Q分别在y轴、x轴上时PO=QO得:6﹣t=8﹣2t,解得t=2(秒),
(ii)当点P、Q都在y轴上时PO=QO得:6﹣t=2t﹣8,解得t=(秒),
(iii)当点P在x轴上,Q在y轴时若二者都没有提前停止,则PO=QO得:t﹣6=2t﹣8,解得t=2(秒)不合题意;
当点Q提前停止时,有t﹣6=6,解得t=12(秒),
综上所述:当两动点运动时间为2、、12秒时,△OPE与△OQF全等
19.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠CAE.
在△ADB和△AEC中,
,
∴△ADB≌AEC(SAS),
∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD.
∴∠3=25°+30°=55°.
答:∠3的度数为55°.
20.(1)证明:在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)证明:∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM,
由(1)得:△ABD≌△ACE,
∴∠B=∠C,
在△ACM和△ABN中,,
∴△ACM≌△ABN(ASA),
∴∠M=∠N.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
