3.2.1 单调性与最大最小值(第1,2课时)课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(36张PPT)
文档属性
| 名称 | 3.2.1 单调性与最大最小值(第1,2课时)课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1002.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 11:23:24 | ||
图片预览








文档简介
3.2.1 单调性与最大最小值
——第一课时
2020.10.19
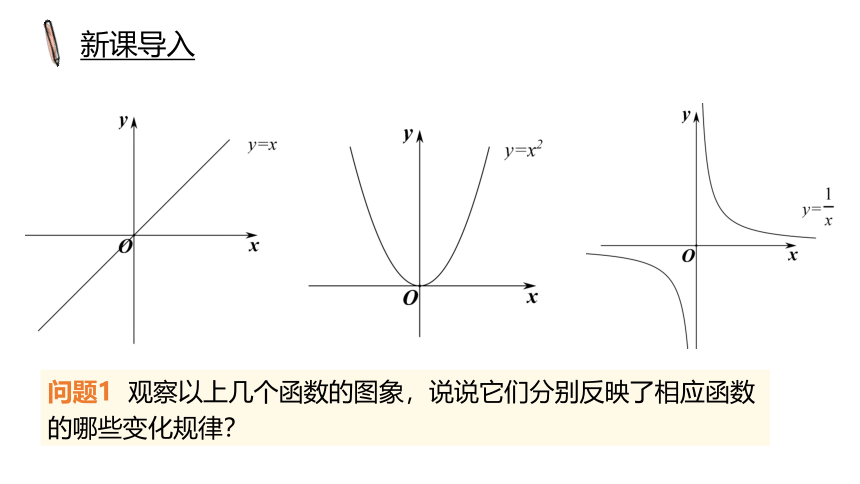
新课导入
问题1 观察以上几个函数的图象,说说它们分别反映了相应函数的哪些变化规律?
设函数的定义域为I,区间 。在区间 D 上,若函数的图象(从左至右看)总是上升的,则称函数在区间D上单调递增;在区间D上,若函数的图象(从左自右看)总是下降的,则称函数在区间D上单调递减。
图形语言定义
问题2 当一个函数在某一个区间上是单调递增(或单调递减)的时候,相应的自变量的值与对应的函数值的变化规律是怎样的呢?也就是如何从数量关系来刻画函数的这种性质?
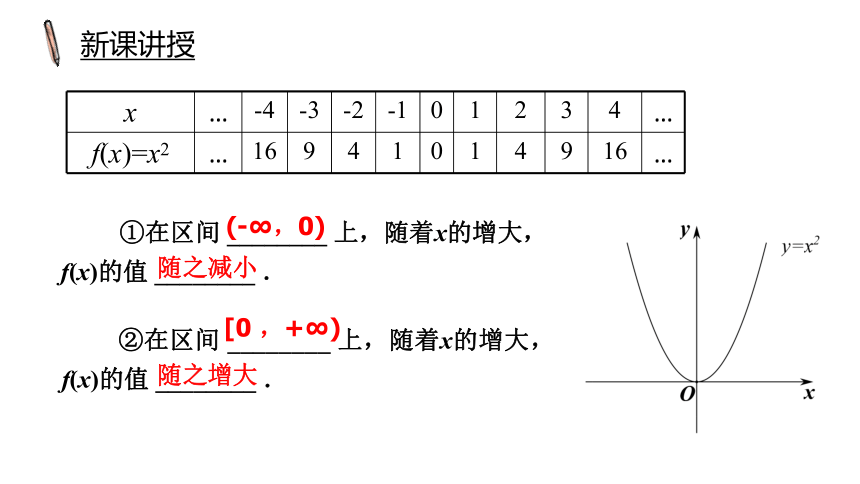
新课讲授
①在区间 ________ 上,随着x的增大,f(x)的值 ________ .
②在区间 ________ 上,随着x的增大,f(x)的值 ________ .
随之减小
(-∞,0)
随之增大
[0 ,+∞)
x
…
-4
-3
-2
-1
0
1
2
3
4
…
f(x)=x2
…
16
9
4
1
0
1
4
9
16
…
在区间D上,若f(x)的值随x的增大而增大,则称函数f(x)在区间D上单调递增;若f(x)的值随x的增大而减小,则称函数f(x)在区间D上单调递减。
描述性定义
问题3 我们如何从函数值的角度证明函数 y=x2 在区间[0,+∞)上单调递增?
问题3 我们如何用从函数值的角度证明函数 y=x2 在区间[0,+∞)上单调递增?
设函数在区间(a,b)上,有无数个自变量,使得当a如果对于区间(a,b)上任意x有f(a)在函数y=x2,x∈[0,+∞)的图象上任意取两点,自变量大的函数值也一定大,能否说明函数在[0,+∞)上单调递增?
“许多个”不能代表“全部”
函数单调性的概念(形式化定义)
特别的,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
一般地,设函数f(x)的定义域为I,区间 :
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递增.
特别的,当函数f(x)在它的定义域上单调递减时,我们就称它是减函数.
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递减.
【注意】
函数的单调性是函数的“局部性质”,它与区间密切相关
思考:仿照单调递增的定义说出单调递减的定义.
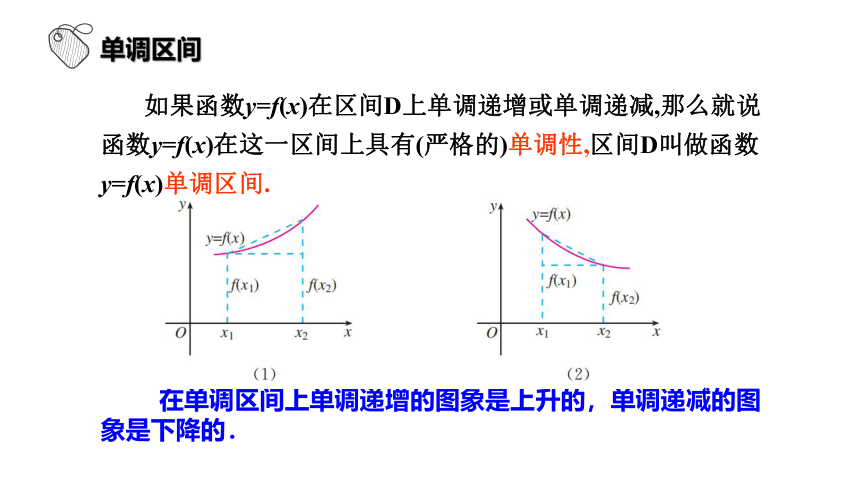
在单调区间上单调递增的图象是上升的,单调递减的图象是下降的.
如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做函数y=f(x)单调区间.
单调区间
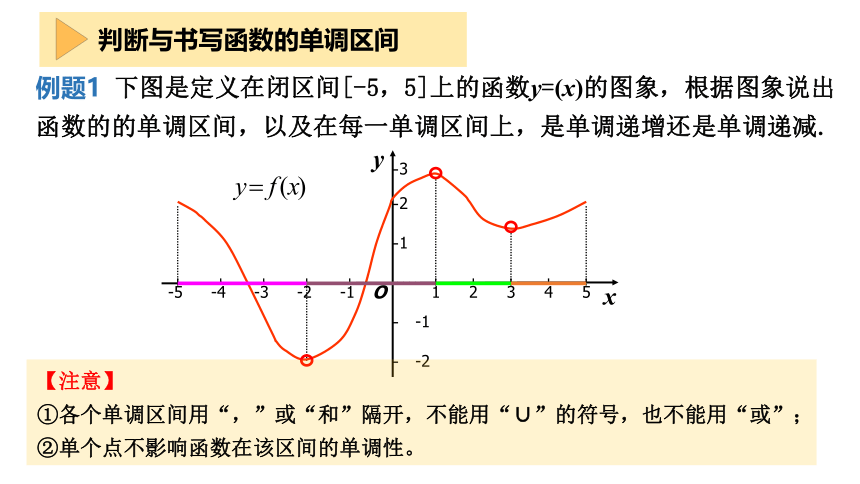
例题1 下图是定义在闭区间[-5,5]上的函数y=(x)的图象,根据图象说出函数的的单调区间,以及在每一单调区间上,是单调递增还是单调递减.
-5
O
x
y
1
2
3
4
5
-1
-2
-3
-4
1
2
3
-1
-2
【注意】
①各个单调区间用“,”或“和”隔开,不能用“∪”的符号,也不能用“或”;
②单个点不影响函数在该区间的单调性。
判断与书写函数的单调区间
练习1.如下图所为函数y=f(x)在[-4,7]的图像,则函数f(x)的单调递增区间是
练习2.某地一天内的气温Q(t)与时刻t之间的关系如下图所示,请写出其单调区间。
利用定义求证函数的单调性
例题2
1.取值:设x1 、x2 是给定区间内的任意两个值,且 x1 <x2 ;
2.作差:作差f (x1) - f (x2) ,并将此差式变形;
3.定号:判断f (x1) - f (x2) 的正负;
4.判断:根据f (x1) - f (x2) 的符号确定其增减性。
证明步骤
例题3
例题4
取值
对勾函数
定号
判断
作差
问题4 请同学们作出反比例函数的图象,并判断:
(1)函数的定义域 I 是什么?
(2)它在定义域 I 上的单调性是怎样的 ? 证明你的结论.
(1)函数单调性的概念
(2)函数单调区间
(3)利用定义证明函数单调性
课堂小结
3.2.1 单调性与最大最小值
——第二课时
函数单调性概念
一般地,设函数f(x)的定义域为I,区间 :
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递增.
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递减.
一般地,设函数f(x)的定义域为I,区间 :
同号递增
异号递增
函数单调性概念辨析
1 定义在(a,b)上的函数f(x),若存在x1,x2∈(a,b),使得x12 定义在(a,b)上的函数f(x),若有无穷多对x1,x2∈(a,b),使得x1×
×
作业本P39 T1
函数单调性概念辨析
5 若f(x)在区间I上为单调递增且 f(x1)< f(x2)(x1,x2∈I),则x16 若f(x)在区间I1上为减函数,在区间I2上也为减函数,则f(x)在区间 上也一定为减函数.
×
√
【注意】若函数 y=f(x)在其定义域内的两个区间I1,I2上都是单调递增(递减)的,不能就认为 y=f(x)在区间 上一定就是单调递增(递减)的.
作业本P39 T1
作业本P40 T13
函数单调性概念辨析
3 对任意的x1,x2∈(a,b),且x1≠x2,当 时,f(x)在(a,b)上为减函数.
4 对任意的x1,x2∈(a,b),且x1≠x2,当 时,f(x)在(a,b)上为减函数.
√
×
作业本P40 T12
例题1
取值
定号
下结论
作差
利用定义求证函数的单调性
对勾函数
对勾函数的图象
对勾函数
对勾函数的图象
一般对勾函数
{5940675A-B579-460E-94D1-54222C63F5DA}函数
函数图象
单调性
利用函数图象判断函数的单调性
在(-∞,+∞)上是减函数
在(-∞,+∞)上是增函数
k>0
k<0
一次函数
y=kx+b(k>0)
{5940675A-B579-460E-94D1-54222C63F5DA}函数
函数图象
单调性
利用函数图象判断函数的单调性
k>0
反比例函数
y=k/x(k≠0)
在(-∞,0)和(0,+∞)上单调递减
在(-∞,0)和(0,+∞)上单调递增
k<0
例题1 函数 和 在 单调递减 ,求m范围.
例题2 下列函数在区间 上是减函数的是________________
利用函数图象判断函数的单调性
x∈[2,+∞)
x∈[-2,+∞)
x∈(-∞,3]
例题3 函数 单调递增区间是_________
变式1 函数 单调递增区间是_________
变式2 函数 单调递增区间是_________
变式3 若函数 在区间
上是单调递减的,则 的取值范围是_________
作业本P39 T8
作业本P39 T6
(-∞,0)和(0,+∞)
(-∞,-1)和(-1,+∞)
{5940675A-B579-460E-94D1-54222C63F5DA}函数
函数图象
单调性
利用函数图象判断函数的单调性
二次函数
y=ax2+bx+c(a≠0)
在 上单调递增
在 上单调递减
在 上单调递减
在 上单调递增
a>0
a<0
开口方向
对称轴
例题4 函数 单调递减区间是____________
单调递增区间是____________
变式1 函数 在区间
上是单调递减的,则 的取值范围是_________
变式2 函数 在区间 上是单调函数,则 的取值范围是_________
作业本P40 T15
(-∞,1]
(1,+∞]
例题5 画出函数 的图象,
并指出函数的单调区间。
作业本P40 T10
单调递增区间:(-∞,-1]和(0,1)
单调递减区间:(-1,0]和(1,+∞)
变式1 函数 单调递减区间是____________单调递增区间是_________
变式2 函数 单调递减区间是____________单调递增区间是_________
作业本P40 T14
周三午测T11
单调性与不等式
作业本P40 T11
作业本P40 T16
周三午测 T10、T18
感谢各位观看
THANK YOU
——第一课时
2020.10.19
新课导入
问题1 观察以上几个函数的图象,说说它们分别反映了相应函数的哪些变化规律?
设函数的定义域为I,区间 。在区间 D 上,若函数的图象(从左至右看)总是上升的,则称函数在区间D上单调递增;在区间D上,若函数的图象(从左自右看)总是下降的,则称函数在区间D上单调递减。
图形语言定义
问题2 当一个函数在某一个区间上是单调递增(或单调递减)的时候,相应的自变量的值与对应的函数值的变化规律是怎样的呢?也就是如何从数量关系来刻画函数的这种性质?
新课讲授
①在区间 ________ 上,随着x的增大,f(x)的值 ________ .
②在区间 ________ 上,随着x的增大,f(x)的值 ________ .
随之减小
(-∞,0)
随之增大
[0 ,+∞)
x
…
-4
-3
-2
-1
0
1
2
3
4
…
f(x)=x2
…
16
9
4
1
0
1
4
9
16
…
在区间D上,若f(x)的值随x的增大而增大,则称函数f(x)在区间D上单调递增;若f(x)的值随x的增大而减小,则称函数f(x)在区间D上单调递减。
描述性定义
问题3 我们如何从函数值的角度证明函数 y=x2 在区间[0,+∞)上单调递增?
问题3 我们如何用从函数值的角度证明函数 y=x2 在区间[0,+∞)上单调递增?
设函数在区间(a,b)上,有无数个自变量,使得当a
“许多个”不能代表“全部”
函数单调性的概念(形式化定义)
特别的,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
一般地,设函数f(x)的定义域为I,区间 :
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递增.
特别的,当函数f(x)在它的定义域上单调递减时,我们就称它是减函数.
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递减.
【注意】
函数的单调性是函数的“局部性质”,它与区间密切相关
思考:仿照单调递增的定义说出单调递减的定义.
在单调区间上单调递增的图象是上升的,单调递减的图象是下降的.
如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做函数y=f(x)单调区间.
单调区间
例题1 下图是定义在闭区间[-5,5]上的函数y=(x)的图象,根据图象说出函数的的单调区间,以及在每一单调区间上,是单调递增还是单调递减.
-5
O
x
y
1
2
3
4
5
-1
-2
-3
-4
1
2
3
-1
-2
【注意】
①各个单调区间用“,”或“和”隔开,不能用“∪”的符号,也不能用“或”;
②单个点不影响函数在该区间的单调性。
判断与书写函数的单调区间
练习1.如下图所为函数y=f(x)在[-4,7]的图像,则函数f(x)的单调递增区间是
练习2.某地一天内的气温Q(t)与时刻t之间的关系如下图所示,请写出其单调区间。
利用定义求证函数的单调性
例题2
1.取值:设x1 、x2 是给定区间内的任意两个值,且 x1 <x2 ;
2.作差:作差f (x1) - f (x2) ,并将此差式变形;
3.定号:判断f (x1) - f (x2) 的正负;
4.判断:根据f (x1) - f (x2) 的符号确定其增减性。
证明步骤
例题3
例题4
取值
对勾函数
定号
判断
作差
问题4 请同学们作出反比例函数的图象,并判断:
(1)函数的定义域 I 是什么?
(2)它在定义域 I 上的单调性是怎样的 ? 证明你的结论.
(1)函数单调性的概念
(2)函数单调区间
(3)利用定义证明函数单调性
课堂小结
3.2.1 单调性与最大最小值
——第二课时
函数单调性概念
一般地,设函数f(x)的定义域为I,区间 :
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递增.
如果 ,当 时,都有 ,那么就称函数f(x)在区间D上单调递减.
一般地,设函数f(x)的定义域为I,区间 :
同号递增
异号递增
函数单调性概念辨析
1 定义在(a,b)上的函数f(x),若存在x1,x2∈(a,b),使得x1
×
作业本P39 T1
函数单调性概念辨析
5 若f(x)在区间I上为单调递增且 f(x1)< f(x2)(x1,x2∈I),则x1
×
√
【注意】若函数 y=f(x)在其定义域内的两个区间I1,I2上都是单调递增(递减)的,不能就认为 y=f(x)在区间 上一定就是单调递增(递减)的.
作业本P39 T1
作业本P40 T13
函数单调性概念辨析
3 对任意的x1,x2∈(a,b),且x1≠x2,当 时,f(x)在(a,b)上为减函数.
4 对任意的x1,x2∈(a,b),且x1≠x2,当 时,f(x)在(a,b)上为减函数.
√
×
作业本P40 T12
例题1
取值
定号
下结论
作差
利用定义求证函数的单调性
对勾函数
对勾函数的图象
对勾函数
对勾函数的图象
一般对勾函数
{5940675A-B579-460E-94D1-54222C63F5DA}函数
函数图象
单调性
利用函数图象判断函数的单调性
在(-∞,+∞)上是减函数
在(-∞,+∞)上是增函数
k>0
k<0
一次函数
y=kx+b(k>0)
{5940675A-B579-460E-94D1-54222C63F5DA}函数
函数图象
单调性
利用函数图象判断函数的单调性
k>0
反比例函数
y=k/x(k≠0)
在(-∞,0)和(0,+∞)上单调递减
在(-∞,0)和(0,+∞)上单调递增
k<0
例题1 函数 和 在 单调递减 ,求m范围.
例题2 下列函数在区间 上是减函数的是________________
利用函数图象判断函数的单调性
x∈[2,+∞)
x∈[-2,+∞)
x∈(-∞,3]
例题3 函数 单调递增区间是_________
变式1 函数 单调递增区间是_________
变式2 函数 单调递增区间是_________
变式3 若函数 在区间
上是单调递减的,则 的取值范围是_________
作业本P39 T8
作业本P39 T6
(-∞,0)和(0,+∞)
(-∞,-1)和(-1,+∞)
{5940675A-B579-460E-94D1-54222C63F5DA}函数
函数图象
单调性
利用函数图象判断函数的单调性
二次函数
y=ax2+bx+c(a≠0)
在 上单调递增
在 上单调递减
在 上单调递减
在 上单调递增
a>0
a<0
开口方向
对称轴
例题4 函数 单调递减区间是____________
单调递增区间是____________
变式1 函数 在区间
上是单调递减的,则 的取值范围是_________
变式2 函数 在区间 上是单调函数,则 的取值范围是_________
作业本P40 T15
(-∞,1]
(1,+∞]
例题5 画出函数 的图象,
并指出函数的单调区间。
作业本P40 T10
单调递增区间:(-∞,-1]和(0,1)
单调递减区间:(-1,0]和(1,+∞)
变式1 函数 单调递减区间是____________单调递增区间是_________
变式2 函数 单调递减区间是____________单调递增区间是_________
作业本P40 T14
周三午测T11
单调性与不等式
作业本P40 T11
作业本P40 T16
周三午测 T10、T18
感谢各位观看
THANK YOU
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
