4.2 指数函数课件- 2020-2021学年高一上学期数学人教A版(2019)必修第一册(38张PPT)
文档属性
| 名称 | 4.2 指数函数课件- 2020-2021学年高一上学期数学人教A版(2019)必修第一册(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 11:37:13 | ||
图片预览









文档简介
4.2 指数函数
2020.11.19
16384根
引例1 拉龙须糖
引例2 《庄子?天下》中写道:“一尺之棰,日取其半,万世不竭”。请你写出 x天后,木棍的剩余长度 y 与天数x 所满足的关系式。
……
尝试归纳这两个特殊对象的共性,总结规律,抽象出一个新的函数模型。
(2)变量在指数的位置
(3)底数为常数
(4)系数为1
y = ax
(1)指数幂的形式
观察这两个函数的解析式的结构特征,与学过的幂函数y=x2的结构有什么区别吗?
问题1
指数函数定义
一般地,函数 y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
思考 定义中为什么要求常数a满足a>0且a≠1?
否则会出现什么情况呢?
①若a=0,则当x >0时,ax=0;
当x ≤ 0时,ax无意义.
②若a<0,则对于x的某些数值,可使ax无意义.
③若a=1,则对于任何x∈R,ax=1,是一个常量,没有研究的必要
为了避免上述各种情况,所以规定a>0且a?1。
思考 定义中为什么要求常数a满足a>0且a≠1?
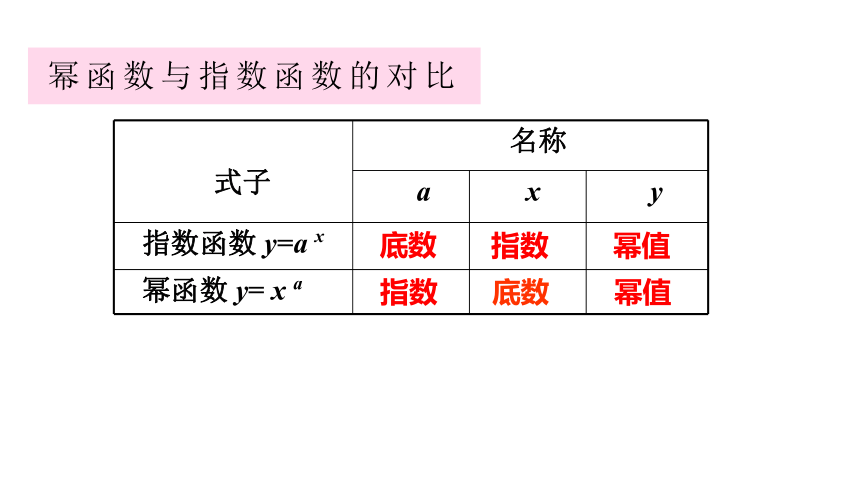
式子
名称
a
x
y
指数函数 y=a x
幂函数 y= x a
底数
指数
指数
底数
幂值
幂值
幂函数与指数函数的对比
例题1 根据指数函数的定义,判断以下例子是否为指数函数。
(1)y=3x
(2)y=x3
(3)y=(-3)x
(4)y=-3x
(5)y=πx
(6)y=(3-π)x
(7)y=32x
(8)y=xx
(9)y=3x+1
(10)y=(2a-1)x(a>1/2且a≠1)
√
√
√
√
练习1 已知 是指数函数,求a的值.
例题2
探究思路
从具体的函数入手(特殊→一般)
定义、图象、性质
(定义域、值域、单调性、奇偶性等)
作出图象?观察特征?得出性质(数形结合)
列表、描点、连线。
问题2 一般情况我们是如何去研究一个函数的?
研究思路
我们一般从哪些方面去研究函数?
如何研究指数函数的图象和性质?
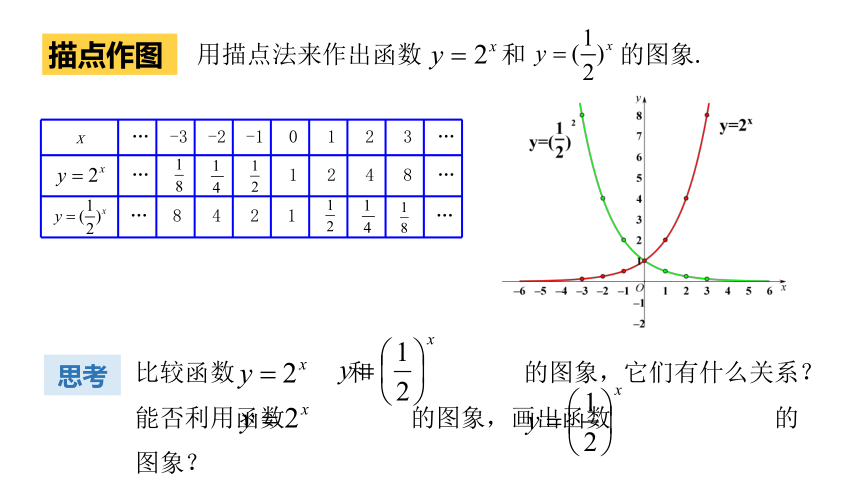
描点法作图象的基本步骤:
用描点法来作出函数
和
的图象.
x
…
-3
-2
-1
0
1
2
3
…
…
1
2
4
8
…
…
8
4
2
1
…
描点作图
思考
比较函数 和 的图象,它们有什么关系?能否利用函数 的图象,画出函数 的图象?
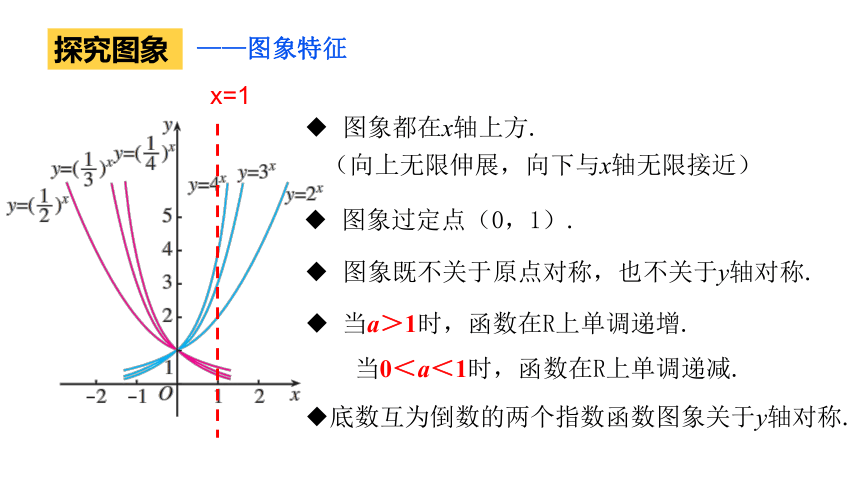
◆ 当a>1时,函数在R上单调递增.
当0<a<1时,函数在R上单调递减.
(向上无限伸展,向下与x轴无限接近)
——图象特征
◆ 图象都在x轴上方.
◆ 图象过定点(0,1).
◆底数互为倒数的两个指数函数图象关于y轴对称.
学生活动
◆ 图象既不关于原点对称,也不关于y轴对称.
探究图象
x=1
?
y=ax(a>1)
y=ax (0图
象
?
?
性
质
?
?
?
?
?
?
(1)定义域: R
(2)值域:(0,+∞)
(3)图象过定点: (0,1)
(4)在R上是单调增函数
在R上是单调减函数
(5)非奇非偶函数
(6)函数y=ax与y=( )x的图象关于y轴对称
O
x
y
y=1
O
x
y
y=1
图象与性质
问题5 通过本节课的学习,你对指数函数有什么认识?你有哪些收获?
1、知识上:指数函数的定义、图像和性质以及应用。关键要抓住底数a>1和0<a<1时函数图象的不同特征和性质。
2、方法上:经历从特殊→一般的认知过程,从观察中获得知识,同时了解指数函数的实际背景和和研究函数的基本方法;体会分类讨论思想、数形结合思想。
课堂小结
例1.如图,试比较a,b,c的大小
指数函数图象性质的应用
式子
名称
a
x
y
指数函数 y=a x
幂函数 y= x a
底数
指数
指数
底数
幂值
幂值
幂函数与指数函数的对比
一般地,函数 y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
a>1
0图
象
性
质
(1)定义域:
(2)值域:
(3)过定点:
(4)单调性:
(4)单调性:
(5)奇偶性:
(5)奇偶性:
R
(0,+∞)
(0,1)
指数函数的图象和性质
增函数
减函数
非奇非偶
非奇非偶
(6)当x>0时,y>1.
当x<0时,0(6)当x>0时,0 当x<0时,y>1.
x
y
o
1
x
y
o
1
例题1 比较下列各题中两个值的大小
利用指数函数单调性比较数的大小
同底——单调性
转换为同底
例题1 比较下列各题中两个值的大小
利用指数函数单调性比较数的大小
指数相同——函数图象——底大图高
转换为同指数
例题1 比较下列各题中两个值的大小
利用指数函数单调性比较数的大小
不同底不同指数——中间量
练习1 比较下列各题中两个值的大小:
>
>
<
<
<
例题2 求下列函数的定义域与值域
指数形复合函数的定义域、值域和单调区间
练习2 求下列函数的定义域与值域
(2)
例题3 求下列函数的单调区间
练习3 求下列函数的单调区间
图象的平移变换:①y=f(x)→y=f(x+a)(左右平移——左加右减)
②y=f(x)→y=f(x)+b(上下平移——上加下减)
图象的对称变换:①y=f(x)→y=f(-x)(关于y轴的对称变换)
②y=f(x)→y=-f(x)(关于x轴的对称变换)
③y=f(x)→y=-f(-x)(关于原点的对称变换)
图象的翻折变换:①y=f(x)→y=|f(x)|
②y=f(x)→y=f(|x|)
函数图象的基本变换
(x轴上方的部分保持不变,x轴下方的部分沿x轴对称地翻折上去)
(y轴右侧的图象保持不变,y轴
左侧的图象去掉,再把y轴右侧的图象沿y轴翻折过去得到)
例题3
指数函数图象的基本变换与应用
练习4
变式
C
D
练习5
变式
D
D
作业本:判断b(a-1)与0的大小关系.
指数函数的综合应用
已知奇偶性求参数值
x∈{x|x≠1},f(-1)=-f(1)
x∈R,f(0)=0
f(-1)=f(1)
x∈R,f(0)=0
f(-1)=-f(1)
例题4
变式1
变式2
变式3
——特殊值法
指数函数的综合应用
ll. 判断函数的奇偶性与单调性
例题5
指数函数的综合应用
lll. 求函数解析式
例题6
指数函数的综合应用
lV. 求函数值域
例题7
指数函数模型的实际应用
1
2
指数函数模型的实际应用
3
4
指数函数模型的实际应用
2020.11.19
16384根
引例1 拉龙须糖
引例2 《庄子?天下》中写道:“一尺之棰,日取其半,万世不竭”。请你写出 x天后,木棍的剩余长度 y 与天数x 所满足的关系式。
……
尝试归纳这两个特殊对象的共性,总结规律,抽象出一个新的函数模型。
(2)变量在指数的位置
(3)底数为常数
(4)系数为1
y = ax
(1)指数幂的形式
观察这两个函数的解析式的结构特征,与学过的幂函数y=x2的结构有什么区别吗?
问题1
指数函数定义
一般地,函数 y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
思考 定义中为什么要求常数a满足a>0且a≠1?
否则会出现什么情况呢?
①若a=0,则当x >0时,ax=0;
当x ≤ 0时,ax无意义.
②若a<0,则对于x的某些数值,可使ax无意义.
③若a=1,则对于任何x∈R,ax=1,是一个常量,没有研究的必要
为了避免上述各种情况,所以规定a>0且a?1。
思考 定义中为什么要求常数a满足a>0且a≠1?
式子
名称
a
x
y
指数函数 y=a x
幂函数 y= x a
底数
指数
指数
底数
幂值
幂值
幂函数与指数函数的对比
例题1 根据指数函数的定义,判断以下例子是否为指数函数。
(1)y=3x
(2)y=x3
(3)y=(-3)x
(4)y=-3x
(5)y=πx
(6)y=(3-π)x
(7)y=32x
(8)y=xx
(9)y=3x+1
(10)y=(2a-1)x(a>1/2且a≠1)
√
√
√
√
练习1 已知 是指数函数,求a的值.
例题2
探究思路
从具体的函数入手(特殊→一般)
定义、图象、性质
(定义域、值域、单调性、奇偶性等)
作出图象?观察特征?得出性质(数形结合)
列表、描点、连线。
问题2 一般情况我们是如何去研究一个函数的?
研究思路
我们一般从哪些方面去研究函数?
如何研究指数函数的图象和性质?
描点法作图象的基本步骤:
用描点法来作出函数
和
的图象.
x
…
-3
-2
-1
0
1
2
3
…
…
1
2
4
8
…
…
8
4
2
1
…
描点作图
思考
比较函数 和 的图象,它们有什么关系?能否利用函数 的图象,画出函数 的图象?
◆ 当a>1时,函数在R上单调递增.
当0<a<1时,函数在R上单调递减.
(向上无限伸展,向下与x轴无限接近)
——图象特征
◆ 图象都在x轴上方.
◆ 图象过定点(0,1).
◆底数互为倒数的两个指数函数图象关于y轴对称.
学生活动
◆ 图象既不关于原点对称,也不关于y轴对称.
探究图象
x=1
?
y=ax(a>1)
y=ax (0
象
?
?
性
质
?
?
?
?
?
?
(1)定义域: R
(2)值域:(0,+∞)
(3)图象过定点: (0,1)
(4)在R上是单调增函数
在R上是单调减函数
(5)非奇非偶函数
(6)函数y=ax与y=( )x的图象关于y轴对称
O
x
y
y=1
O
x
y
y=1
图象与性质
问题5 通过本节课的学习,你对指数函数有什么认识?你有哪些收获?
1、知识上:指数函数的定义、图像和性质以及应用。关键要抓住底数a>1和0<a<1时函数图象的不同特征和性质。
2、方法上:经历从特殊→一般的认知过程,从观察中获得知识,同时了解指数函数的实际背景和和研究函数的基本方法;体会分类讨论思想、数形结合思想。
课堂小结
例1.如图,试比较a,b,c的大小
指数函数图象性质的应用
式子
名称
a
x
y
指数函数 y=a x
幂函数 y= x a
底数
指数
指数
底数
幂值
幂值
幂函数与指数函数的对比
一般地,函数 y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
a>1
0
象
性
质
(1)定义域:
(2)值域:
(3)过定点:
(4)单调性:
(4)单调性:
(5)奇偶性:
(5)奇偶性:
R
(0,+∞)
(0,1)
指数函数的图象和性质
增函数
减函数
非奇非偶
非奇非偶
(6)当x>0时,y>1.
当x<0时,0
x
y
o
1
x
y
o
1
例题1 比较下列各题中两个值的大小
利用指数函数单调性比较数的大小
同底——单调性
转换为同底
例题1 比较下列各题中两个值的大小
利用指数函数单调性比较数的大小
指数相同——函数图象——底大图高
转换为同指数
例题1 比较下列各题中两个值的大小
利用指数函数单调性比较数的大小
不同底不同指数——中间量
练习1 比较下列各题中两个值的大小:
>
>
<
<
<
例题2 求下列函数的定义域与值域
指数形复合函数的定义域、值域和单调区间
练习2 求下列函数的定义域与值域
(2)
例题3 求下列函数的单调区间
练习3 求下列函数的单调区间
图象的平移变换:①y=f(x)→y=f(x+a)(左右平移——左加右减)
②y=f(x)→y=f(x)+b(上下平移——上加下减)
图象的对称变换:①y=f(x)→y=f(-x)(关于y轴的对称变换)
②y=f(x)→y=-f(x)(关于x轴的对称变换)
③y=f(x)→y=-f(-x)(关于原点的对称变换)
图象的翻折变换:①y=f(x)→y=|f(x)|
②y=f(x)→y=f(|x|)
函数图象的基本变换
(x轴上方的部分保持不变,x轴下方的部分沿x轴对称地翻折上去)
(y轴右侧的图象保持不变,y轴
左侧的图象去掉,再把y轴右侧的图象沿y轴翻折过去得到)
例题3
指数函数图象的基本变换与应用
练习4
变式
C
D
练习5
变式
D
D
作业本:判断b(a-1)与0的大小关系.
指数函数的综合应用
已知奇偶性求参数值
x∈{x|x≠1},f(-1)=-f(1)
x∈R,f(0)=0
f(-1)=f(1)
x∈R,f(0)=0
f(-1)=-f(1)
例题4
变式1
变式2
变式3
——特殊值法
指数函数的综合应用
ll. 判断函数的奇偶性与单调性
例题5
指数函数的综合应用
lll. 求函数解析式
例题6
指数函数的综合应用
lV. 求函数值域
例题7
指数函数模型的实际应用
1
2
指数函数模型的实际应用
3
4
指数函数模型的实际应用
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
