4.5.1函数的零点与方程的解课件- 2020-2021学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.5.1函数的零点与方程的解课件- 2020-2021学年高一上学期数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 819.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 11:39:34 | ||
图片预览







文档简介
2020.12.3
新课导入
问题1 求下列方程的解.
隋唐数学家王孝通
7世纪,隋唐数学家王孝通找出了求三次方程正根的数值解法
北宋数学家贾宪
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法
南宋数学家秦九韶
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法
9世纪,阿拉伯数学家花拉子米给出了一次方程和二次方程的一般解法.
1541年,意大利数学家塔尔塔利亚给出了三次方程的一般解法.
1545年,意大利数学家卡尔达诺的《大术》一书中,记载了费拉里的四次方程的一般解法.
19世纪挪威数学家阿贝尔证明了五次及五次以上代数方程没有根式解.指数方程、对数方程等超越方程也没有求根公式.
新课导入
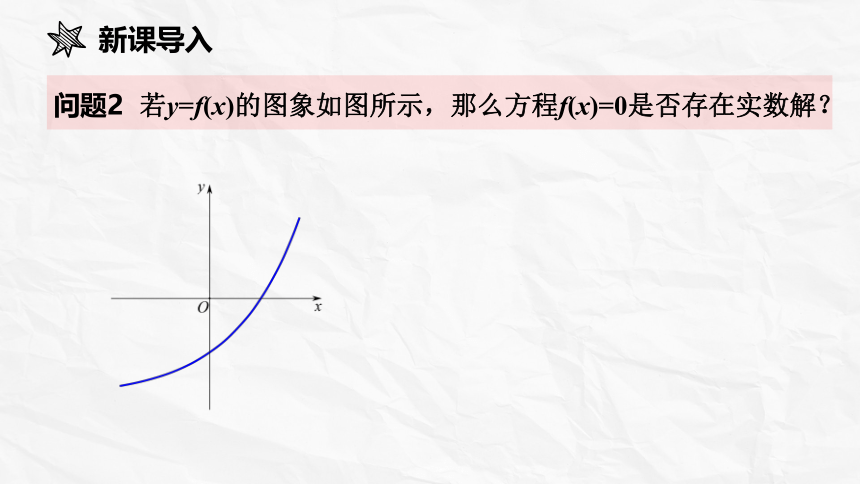
问题2 若y=f(x)的图象如图所示,那么方程f(x)=0是否存在实数解?
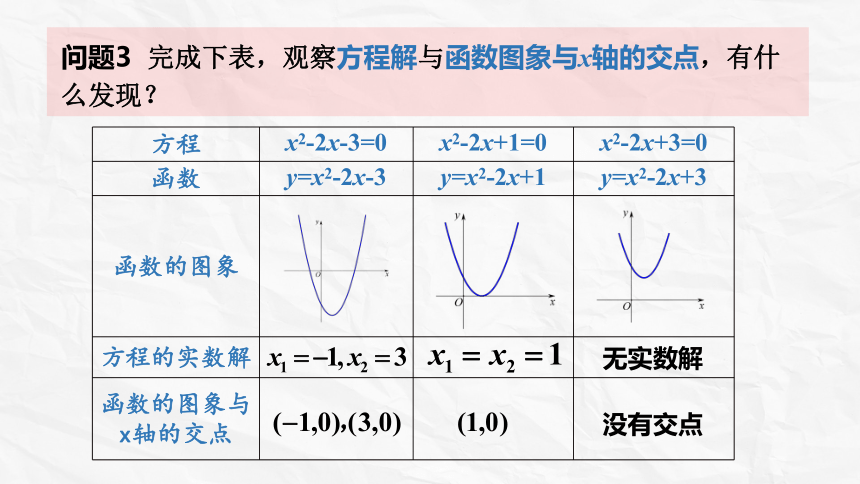
问题3 完成下表,观察方程解与函数图象与x轴的交点,有什么发现?
{5940675A-B579-460E-94D1-54222C63F5DA}方程
x2-2x-3=0
x2-2x+1=0
x2-2x+3=0
函数
y=x2-2x-3
y=x2-2x+1
y=x2-2x+3
函数的图象
方程的实数解
函数的图象与x轴的交点
无实数解
没有交点
新课讲授——
P50 一般地,对于二次函数y=ax2+bx+c,我们把使ax2+bx+c=0的实数x叫做二次函数y=ax2+bx+c的零点.
与二次函数的零点一样,对于一般函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数y=f(x)的零点
函数y=f(x)与x轴交点的横坐标
方程f(x)=0的实数解
形
数
特殊
一般
牛刀小试
练一练 请画出下列函数的简易图象,判断其是否有零点,并求出其零点.
注意:零点是一个实数,是指函数与x轴交点的横坐标
问题4 求方程lnx+2x-6=0的实数解.
方程lnx+2x-6=0是否存在实数解?如果有,有几个?
超越方程
大部分的超越方程只能求出近似解
求超越方程的近似解:二分法,迭代法,牛顿法,割线法,二次插值法,切比雪夫迭代法……
问题5 观察二次函数f(x)=x2-2x-3的图象,想一想,两个零点附近函数值变化有什么特点?
(1)在[-2,1]上,我们发现函数f(x)在区间(-2,1)内有零点x=_______,有f(-2)_____0,f(1)_____0,得到 f(-2)·f(1)_____0(填>或<)
(2)在[2,4]上,我们发现函数f(x)在区间(2,4)内有零点x=_______,有f(2)_____0,f(4)_____0,得到 f(2)·f(4)_____0(填>或<)
问题6 通过(1)(2)的探索,你是否可以归纳出f(x)在[a,b]上满足怎么样的条件时,f(x)在[a,b]上存在零点.
3
问题6 通过(1)(2)的探索,你是否可以归纳出f(x)在[a,b]满足怎么样的条件时,f(x)在[a,b]上存在零点.
练一练 f(x)= ex+4x的零点所在区域为( )
如果函数y=f(x)在区间[a,b]上满足f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点. 即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
问题4 方程lnx+2x-6=0是否存在实数根?如果有,有几个?
定理辨析:判断正误
(1)若f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内有零点.
(2)若函数y=f(x)在区间(a,b)内有零点,则有f(a)·f(b)<0.
(3)若f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内只有一个零点.
函数零点存在定理的三个注意点:
1、函数在区间上是连续的;
(1)
(2)
(3)
2、定理不可逆——函数零点存在定理为一充分不必要条件;
3、至少只存在一个零点。
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内至少有一个零点. 即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
新课讲授
问题7 观察如下三个函数图象,想一想,函数要满足什么条件在区间[a,b]上只有一个零点?
如果函数y=f(x)在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异,即f(a)·f(b)<0,且是单调函数. 那么,这个函数在(a,b)内必有唯一的一个零点.
例题巩固
例题1 判断下列函数在给定区间内是否有零点.
(1) f(x)=x2-2x-2在[1,2]上有零点吗?
(2) f(x)=-x2+4x-3在[2,4]上有零点吗?
通过本节课的学习,你学到了哪些知识?你能解决哪些问题?
通过本节课的学习,你体会到哪些数学思想方法?
需要进一步研究的问题是什么?
课堂小结
复习回顾
函数y=f(x)的零点
函数y=f(x)与x轴交点的横坐标
方程f(x)=0的实数解
形
数
注意:零点是一个实数,是指函数与x轴交点的横坐标
1、函数的零点的定义:
使 的实数 叫做函数 的零点
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内至少有一个零点. 即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
复习回顾
2、函数零点存在定理:
例题巩固
函数零点存在性判断
A
例题1
作业本P79 T7
问题7 观察如下三个函数图象,想一想,函数要满足什么条件在区间[a,b]上只有一个零点?
如果函数y=f(x)在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异,即f(a)·f(b)<0,且是单调函数. 那么,这个函数在(a,b)内必有唯一的一个零点.
例题巩固
函数零点个数判断
1、利用函数零点存在定理
作业本P79 T3、T9、T11
例题2
例题巩固
例题3 函数 f(x)=2x|log0.5x|-1的零点个数为( )
A.1 B.2 C.3 D.4
2、代数法:求方程f(x)=0的实数解
作业本P79 T1、T10
3、数形结合法:借助函数图象
1、利用函数零点存在定理
例题巩固
已知函数 ,函数 ,则函数 的零点个数为_________.
练习1
例题巩固
函数零点的综合应用
二次函数根的分布
例题4
作业本P79 T5
例题巩固
关于x的方程ax2-2(a+1)x+a-1=0,求a为何值时:
(1)方程有一根;
(2)方程有一正一负根;
(3) 一根大于1,一根小于1;
(4) 两根都大于1.
二次函数根的分布
练习2
新课导入
问题1 求下列方程的解.
隋唐数学家王孝通
7世纪,隋唐数学家王孝通找出了求三次方程正根的数值解法
北宋数学家贾宪
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法
南宋数学家秦九韶
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法
9世纪,阿拉伯数学家花拉子米给出了一次方程和二次方程的一般解法.
1541年,意大利数学家塔尔塔利亚给出了三次方程的一般解法.
1545年,意大利数学家卡尔达诺的《大术》一书中,记载了费拉里的四次方程的一般解法.
19世纪挪威数学家阿贝尔证明了五次及五次以上代数方程没有根式解.指数方程、对数方程等超越方程也没有求根公式.
新课导入
问题2 若y=f(x)的图象如图所示,那么方程f(x)=0是否存在实数解?
问题3 完成下表,观察方程解与函数图象与x轴的交点,有什么发现?
{5940675A-B579-460E-94D1-54222C63F5DA}方程
x2-2x-3=0
x2-2x+1=0
x2-2x+3=0
函数
y=x2-2x-3
y=x2-2x+1
y=x2-2x+3
函数的图象
方程的实数解
函数的图象与x轴的交点
无实数解
没有交点
新课讲授——
P50 一般地,对于二次函数y=ax2+bx+c,我们把使ax2+bx+c=0的实数x叫做二次函数y=ax2+bx+c的零点.
与二次函数的零点一样,对于一般函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数y=f(x)的零点
函数y=f(x)与x轴交点的横坐标
方程f(x)=0的实数解
形
数
特殊
一般
牛刀小试
练一练 请画出下列函数的简易图象,判断其是否有零点,并求出其零点.
注意:零点是一个实数,是指函数与x轴交点的横坐标
问题4 求方程lnx+2x-6=0的实数解.
方程lnx+2x-6=0是否存在实数解?如果有,有几个?
超越方程
大部分的超越方程只能求出近似解
求超越方程的近似解:二分法,迭代法,牛顿法,割线法,二次插值法,切比雪夫迭代法……
问题5 观察二次函数f(x)=x2-2x-3的图象,想一想,两个零点附近函数值变化有什么特点?
(1)在[-2,1]上,我们发现函数f(x)在区间(-2,1)内有零点x=_______,有f(-2)_____0,f(1)_____0,得到 f(-2)·f(1)_____0(填>或<)
(2)在[2,4]上,我们发现函数f(x)在区间(2,4)内有零点x=_______,有f(2)_____0,f(4)_____0,得到 f(2)·f(4)_____0(填>或<)
问题6 通过(1)(2)的探索,你是否可以归纳出f(x)在[a,b]上满足怎么样的条件时,f(x)在[a,b]上存在零点.
3
问题6 通过(1)(2)的探索,你是否可以归纳出f(x)在[a,b]满足怎么样的条件时,f(x)在[a,b]上存在零点.
练一练 f(x)= ex+4x的零点所在区域为( )
如果函数y=f(x)在区间[a,b]上满足f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点. 即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
问题4 方程lnx+2x-6=0是否存在实数根?如果有,有几个?
定理辨析:判断正误
(1)若f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内有零点.
(2)若函数y=f(x)在区间(a,b)内有零点,则有f(a)·f(b)<0.
(3)若f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内只有一个零点.
函数零点存在定理的三个注意点:
1、函数在区间上是连续的;
(1)
(2)
(3)
2、定理不可逆——函数零点存在定理为一充分不必要条件;
3、至少只存在一个零点。
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内至少有一个零点. 即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
新课讲授
问题7 观察如下三个函数图象,想一想,函数要满足什么条件在区间[a,b]上只有一个零点?
如果函数y=f(x)在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异,即f(a)·f(b)<0,且是单调函数. 那么,这个函数在(a,b)内必有唯一的一个零点.
例题巩固
例题1 判断下列函数在给定区间内是否有零点.
(1) f(x)=x2-2x-2在[1,2]上有零点吗?
(2) f(x)=-x2+4x-3在[2,4]上有零点吗?
通过本节课的学习,你学到了哪些知识?你能解决哪些问题?
通过本节课的学习,你体会到哪些数学思想方法?
需要进一步研究的问题是什么?
课堂小结
复习回顾
函数y=f(x)的零点
函数y=f(x)与x轴交点的横坐标
方程f(x)=0的实数解
形
数
注意:零点是一个实数,是指函数与x轴交点的横坐标
1、函数的零点的定义:
使 的实数 叫做函数 的零点
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内至少有一个零点. 即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
复习回顾
2、函数零点存在定理:
例题巩固
函数零点存在性判断
A
例题1
作业本P79 T7
问题7 观察如下三个函数图象,想一想,函数要满足什么条件在区间[a,b]上只有一个零点?
如果函数y=f(x)在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异,即f(a)·f(b)<0,且是单调函数. 那么,这个函数在(a,b)内必有唯一的一个零点.
例题巩固
函数零点个数判断
1、利用函数零点存在定理
作业本P79 T3、T9、T11
例题2
例题巩固
例题3 函数 f(x)=2x|log0.5x|-1的零点个数为( )
A.1 B.2 C.3 D.4
2、代数法:求方程f(x)=0的实数解
作业本P79 T1、T10
3、数形结合法:借助函数图象
1、利用函数零点存在定理
例题巩固
已知函数 ,函数 ,则函数 的零点个数为_________.
练习1
例题巩固
函数零点的综合应用
二次函数根的分布
例题4
作业本P79 T5
例题巩固
关于x的方程ax2-2(a+1)x+a-1=0,求a为何值时:
(1)方程有一根;
(2)方程有一正一负根;
(3) 一根大于1,一根小于1;
(4) 两根都大于1.
二次函数根的分布
练习2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
