3.1.2 函数的表示法课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(24张PPT)
文档属性
| 名称 | 3.1.2 函数的表示法课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 11:35:21 | ||
图片预览





文档简介
——第一课时
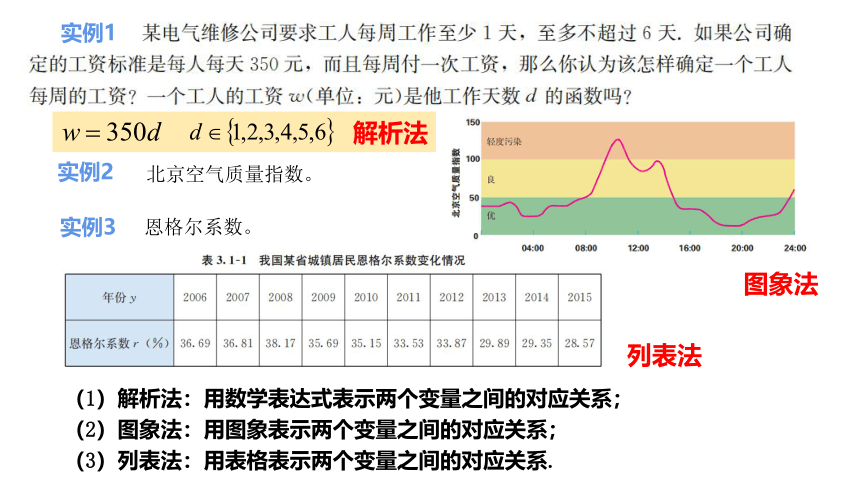
实例1
实例2
北京空气质量指数。
实例3
恩格尔系数。
解析法
图象法
列表法
(1)解析法:用数学表达式表示两个变量之间的对应关系;
(2)图象法:用图象表示两个变量之间的对应关系;
(3)列表法:用表格表示两个变量之间的对应关系.
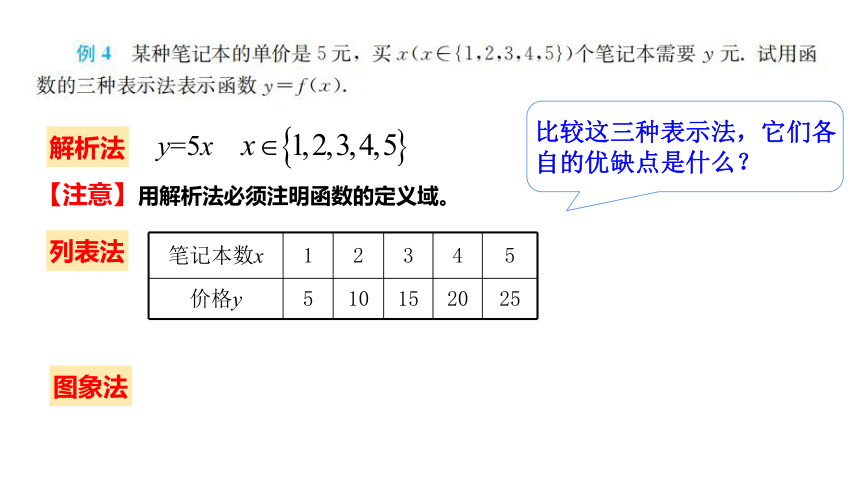
解析法
y=5x
【注意】用解析法必须注明函数的定义域。
列表法
笔记本数x
1
2
3
4
5
价格y
5
10
15
20
25
图象法
比较这三种表示法,它们各自的优缺点是什么?
比较这三种表示法,它们各自的优缺点是什么?
1、解析法:
2、图象法:
3、列表法:
①关系清楚;②容易求解;③便于研究函数的性质。
能直观形象地表示当自变量发生变化时相应函数值的变化趋势。
不必计算就可以直接看出与自变量的值相对应的函数值。
缺点:函数值随自变量变化的规律不直观。
而且不是所有的函数都有解析式。
缺点:它只能表示自变量较少的有限值的对应关系。
缺点:它只能近似地求出自变量所对应的函数值。
1
2
6
3
4
5
60
70
80
90
100
y
x
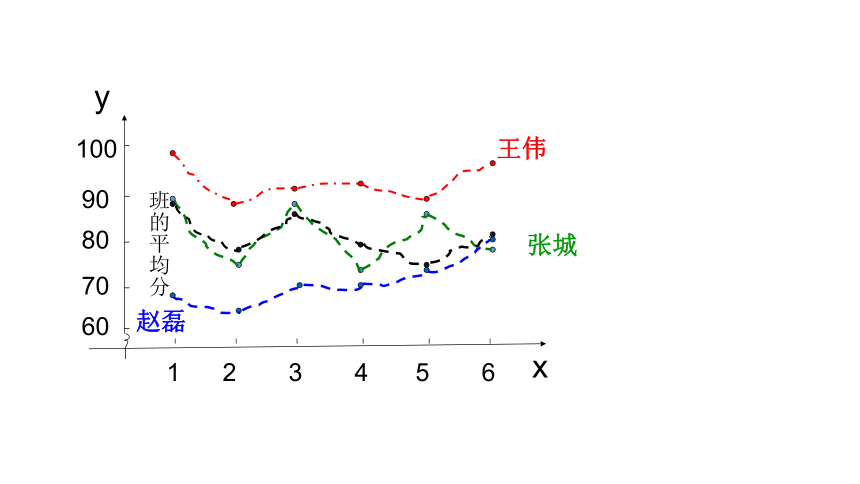
王伟
张城
班的平均分
赵磊
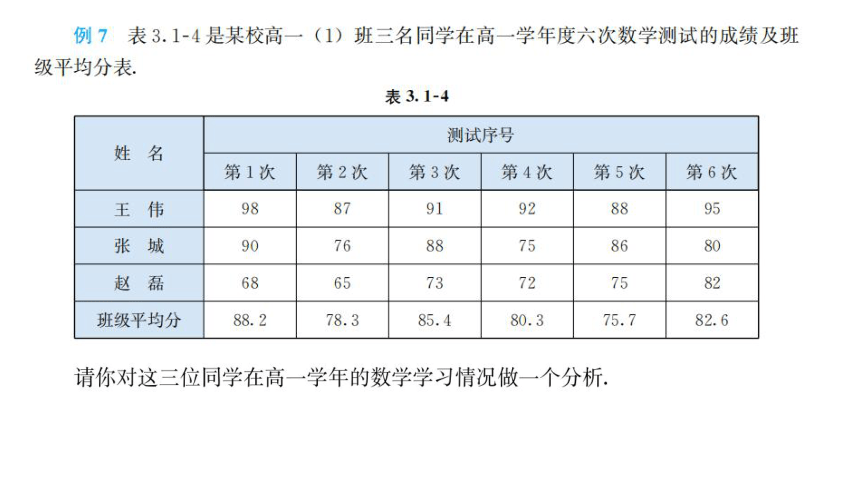
1.有些函数既可用列表法表示,也可用图像法或解析法表示.
2.函数的图象通常是一段或几段光滑的曲线,但有时也可以由一些孤立点或几段线段组成。必须根据定义域画图,利用描点法或图象变换法。
【注意】
要点一 待定系数法求函数解析式
例1 (1)已知反比例函数f(x)满足 f(3)=-6,求f(x)的解析式;
(2)一次函数y=f(x),f(1)=1,f(-1)=-3,求f(x).
解 设一次函数f(x)=ax+b(a≠0),
∵f(1)=1,f(-1)=-3,
规律方法 待定系数法求函数解析式的步骤如下:
(1)设出所求函数含有待定系数的解析式.
如一次函数解析式设为f(x)=ax+b(a≠0),反比例函数解析式设为f(x)= (k≠0),二次函数解析式设为f(x)=ax2+bx+c(a≠0).
(2)把已知条件代入解析式,列出含待定系数的方程或方程组.
(3)解方程或方程组,得到待定系数的值.
(4)将所求待定系数的值代回原式.
例2
要点二:代入法求函数解析式
规律方法 代入法求函数解析式:
告诉你f (x)的解析式,让你求f(狗),将狗整体代入到f (x)的解析式中。
要点三:配凑法、换元法求函数解析式。
例2(1)
(2) 已知函数f(x+1)=x2-2x,则f(x)=__________.
【解析】方法一 (换元法)
令x+1=t,则x=t-1,可得
f(t)=(t-1)2-2(t-1)=t2-4t+3,即f(x)=x2-4x+3.
方法二 (配凑法)
∵x2-2x=(x2+2x+1)-(4x+4)+3=(x+1)2-4(x+1)+3
∴f(x+1)=(x+1)2-4(x+1)+3,即f(x)=x2-4x+3.
x2-4x+3
规律方法 (1)已知f[g(x)]求f(x)型,用换元法或配凑法。
(2)注意定义域的变化(换元后注意新元的取值范围).
换元法解题步骤
例3 (1)若f (x)+2f (-x)=5x+1,求f (x)的表达式.
要点四 方程组法求函数解析式
(2)若 ,求f (x)的表达式.
课堂小结
1.函数三种表示法及其优缺点
2.描点法画函数图象的步骤:
(1)求函数定义域;(2)化简解析式;(3)列表;(4)描点;(5)连线 .
3.求函数解析式常用的方法有:
(1)待定系数法;(2)代入法;(3)换元法;(4)配凑法;(5)方程组法等.
——第二课时
分段函数
法一:描点法;
法二:利用绝对值的意义去绝对值;
分段函数 对于自变量x的不同取值范围,有着不同的函数解析式。
问题1 画出函数y=|x|的图象。
【注意】(1)分段函数是一个函数,而不是几个函数。
(2)分段函数在书写时用大括号把各段函数合并写成一个函数的形式,并且必须指明各段函数自变量的取值范围.
绝对值函数
分段函数
去绝对值
【注意】(1)分段函数的定义域是各段“定义域”的并集;
(2)分段函数值域是各段“值域”的并集;
(3)写定义域时,区间的端点需不重不漏.
例题1 已知 .
要点一:分段函数的图象及应用
(1)画出函数的图象;
(2)求函数的定义域和值域。
要点二:分段函数的求值问题
例题2
注意自变量的值所在的范围,带入相应的解析式求解.
分段利用函数解析式进行求解,但要注意检验其适用范围——分类讨论.
例题4 已知函数 .
例题3 已知函数 ,若f(a)<-3,则a的取值范围是_______ .
例题5 某客运公司确定车票价格的方法是:如果行程不超过100千米,票价是每千米0.5元;如果超过100千米,超过部分按每千米0.4元定价,则客运票价y(元)与行程x(千米)之间的函数关系式是_________.
解析 由题意得,当0≤x≤100时,y=0.5x;
当x>100时y=100×0.5+(x-100)×0.4=10+0.4x.
要点三:分段函数的应用问题
作业本题目解析
(3)根据下列函数的图象写出函数解析式
1
1
1
-1
1
-1
2
-1
实例1
实例2
北京空气质量指数。
实例3
恩格尔系数。
解析法
图象法
列表法
(1)解析法:用数学表达式表示两个变量之间的对应关系;
(2)图象法:用图象表示两个变量之间的对应关系;
(3)列表法:用表格表示两个变量之间的对应关系.
解析法
y=5x
【注意】用解析法必须注明函数的定义域。
列表法
笔记本数x
1
2
3
4
5
价格y
5
10
15
20
25
图象法
比较这三种表示法,它们各自的优缺点是什么?
比较这三种表示法,它们各自的优缺点是什么?
1、解析法:
2、图象法:
3、列表法:
①关系清楚;②容易求解;③便于研究函数的性质。
能直观形象地表示当自变量发生变化时相应函数值的变化趋势。
不必计算就可以直接看出与自变量的值相对应的函数值。
缺点:函数值随自变量变化的规律不直观。
而且不是所有的函数都有解析式。
缺点:它只能表示自变量较少的有限值的对应关系。
缺点:它只能近似地求出自变量所对应的函数值。
1
2
6
3
4
5
60
70
80
90
100
y
x
王伟
张城
班的平均分
赵磊
1.有些函数既可用列表法表示,也可用图像法或解析法表示.
2.函数的图象通常是一段或几段光滑的曲线,但有时也可以由一些孤立点或几段线段组成。必须根据定义域画图,利用描点法或图象变换法。
【注意】
要点一 待定系数法求函数解析式
例1 (1)已知反比例函数f(x)满足 f(3)=-6,求f(x)的解析式;
(2)一次函数y=f(x),f(1)=1,f(-1)=-3,求f(x).
解 设一次函数f(x)=ax+b(a≠0),
∵f(1)=1,f(-1)=-3,
规律方法 待定系数法求函数解析式的步骤如下:
(1)设出所求函数含有待定系数的解析式.
如一次函数解析式设为f(x)=ax+b(a≠0),反比例函数解析式设为f(x)= (k≠0),二次函数解析式设为f(x)=ax2+bx+c(a≠0).
(2)把已知条件代入解析式,列出含待定系数的方程或方程组.
(3)解方程或方程组,得到待定系数的值.
(4)将所求待定系数的值代回原式.
例2
要点二:代入法求函数解析式
规律方法 代入法求函数解析式:
告诉你f (x)的解析式,让你求f(狗),将狗整体代入到f (x)的解析式中。
要点三:配凑法、换元法求函数解析式。
例2(1)
(2) 已知函数f(x+1)=x2-2x,则f(x)=__________.
【解析】方法一 (换元法)
令x+1=t,则x=t-1,可得
f(t)=(t-1)2-2(t-1)=t2-4t+3,即f(x)=x2-4x+3.
方法二 (配凑法)
∵x2-2x=(x2+2x+1)-(4x+4)+3=(x+1)2-4(x+1)+3
∴f(x+1)=(x+1)2-4(x+1)+3,即f(x)=x2-4x+3.
x2-4x+3
规律方法 (1)已知f[g(x)]求f(x)型,用换元法或配凑法。
(2)注意定义域的变化(换元后注意新元的取值范围).
换元法解题步骤
例3 (1)若f (x)+2f (-x)=5x+1,求f (x)的表达式.
要点四 方程组法求函数解析式
(2)若 ,求f (x)的表达式.
课堂小结
1.函数三种表示法及其优缺点
2.描点法画函数图象的步骤:
(1)求函数定义域;(2)化简解析式;(3)列表;(4)描点;(5)连线 .
3.求函数解析式常用的方法有:
(1)待定系数法;(2)代入法;(3)换元法;(4)配凑法;(5)方程组法等.
——第二课时
分段函数
法一:描点法;
法二:利用绝对值的意义去绝对值;
分段函数 对于自变量x的不同取值范围,有着不同的函数解析式。
问题1 画出函数y=|x|的图象。
【注意】(1)分段函数是一个函数,而不是几个函数。
(2)分段函数在书写时用大括号把各段函数合并写成一个函数的形式,并且必须指明各段函数自变量的取值范围.
绝对值函数
分段函数
去绝对值
【注意】(1)分段函数的定义域是各段“定义域”的并集;
(2)分段函数值域是各段“值域”的并集;
(3)写定义域时,区间的端点需不重不漏.
例题1 已知 .
要点一:分段函数的图象及应用
(1)画出函数的图象;
(2)求函数的定义域和值域。
要点二:分段函数的求值问题
例题2
注意自变量的值所在的范围,带入相应的解析式求解.
分段利用函数解析式进行求解,但要注意检验其适用范围——分类讨论.
例题4 已知函数 .
例题3 已知函数 ,若f(a)<-3,则a的取值范围是_______ .
例题5 某客运公司确定车票价格的方法是:如果行程不超过100千米,票价是每千米0.5元;如果超过100千米,超过部分按每千米0.4元定价,则客运票价y(元)与行程x(千米)之间的函数关系式是_________.
解析 由题意得,当0≤x≤100时,y=0.5x;
当x>100时y=100×0.5+(x-100)×0.4=10+0.4x.
要点三:分段函数的应用问题
作业本题目解析
(3)根据下列函数的图象写出函数解析式
1
1
1
-1
1
-1
2
-1
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
