3.2.2 奇偶性课件- 2020-2021学年高一上学期数学人教A版(2019)必修第一册(28张PPT)
文档属性
| 名称 | 3.2.2 奇偶性课件- 2020-2021学年高一上学期数学人教A版(2019)必修第一册(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 14:29:32 | ||
图片预览





文档简介
3.2.2 奇偶性
——第一课时
2020.10.22
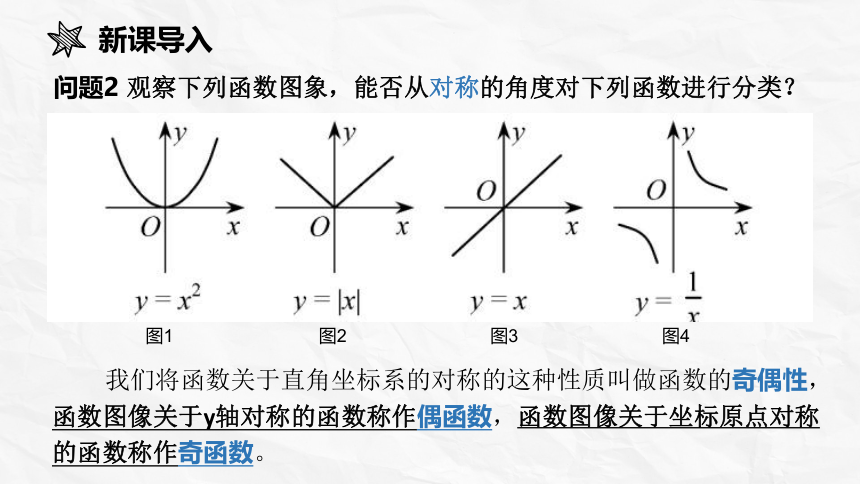
图1
图2
图3
图4
新课导入
问题1 轴对称图形与中心对称图形的实质是什么?
轴对称图形 平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
中心对称图形 在平面内,把一个图形绕着某个点旋转180°,旋转后的图形能与原来的图形重合。
图1
图2
图3
图4
新课导入
问题2 观察下列函数图象,能否从对称的角度对下列函数进行分类?
我们将函数关于直角坐标系的对称的这种性质叫做函数的奇偶性,函数图像关于y轴对称的函数称作偶函数,函数图像关于坐标原点对称的函数称作奇函数。
问题3 函数 是否具有奇偶性?如果有奇偶性,是奇函数还是偶函数?
问题4 如何用数量关系刻画函数的奇偶性?
新课导入
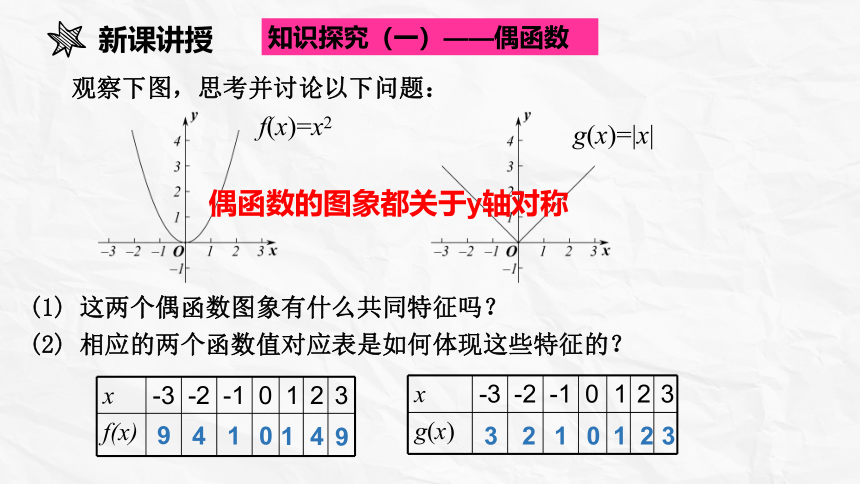
观察下图,思考并讨论以下问题:
(1) 这两个偶函数图象有什么共同特征吗?
(2) 相应的两个函数值对应表是如何体现这些特征的?
x
-3
-2
-1
0
1
2
3
f(x)
x
-3
-2
-1
0
1
2
3
g(x)
9
4
1
0
1
4
9
1
3
2
0
1
2
3
新课讲授
知识探究(一)——偶函数
f(x)=x2
g(x)=|x|
偶函数的图象都关于y轴对称
(3) 什么是偶函数?
f(x)=x2
g(x)=|x|
定义
思考?函数f(x)=x2 , x∈[-1,2]是偶函数吗?偶函数的定义域有什么特征?
定义域关于原点对称
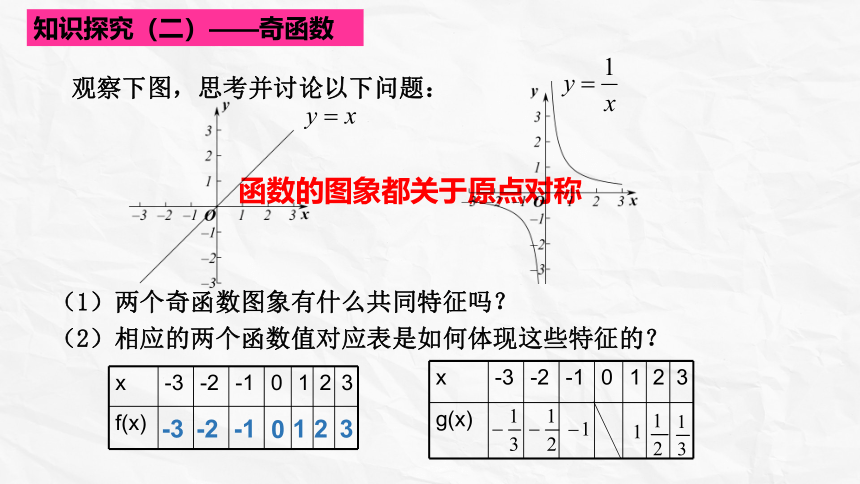
(1)两个奇函数图象有什么共同特征吗?
函数的图象都关于原点对称
(2)相应的两个函数值对应表是如何体现这些特征的?
x
-3
-2
-1
0
1
2
3
f(x)
x
-3
-2
-1
0
1
2
3
g(x)
-3
-2
-1
0
1
2
3
知识探究(二)——奇函数
观察下图,思考并讨论以下问题:
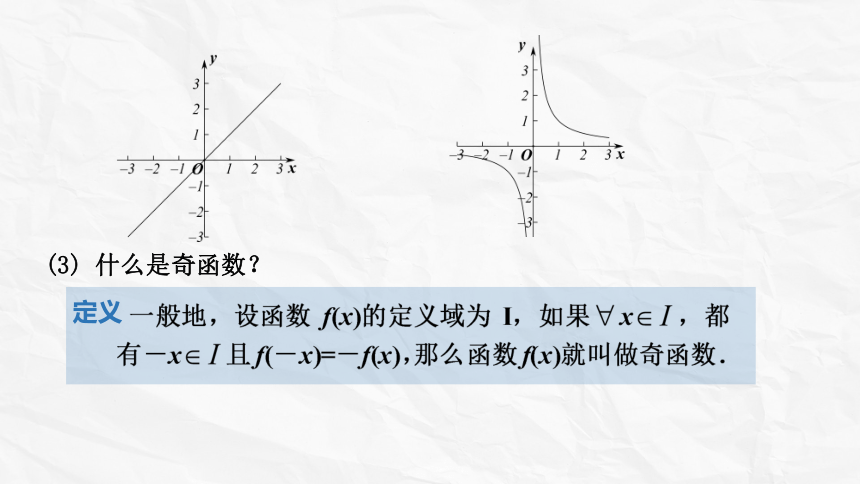
(3) 什么是奇函数?
定义
思考?设函数 是奇函数,且在 处有定义,则
思考?函数f(x)=x , x∈[-1,2]是奇函数吗?奇函数的定义域有什么特征?
定义域关于原点对称
函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则有f(-x)=-f(x)成立.
若f(x)为偶函数,则有f(-x)=f(x)成立.
对奇函数、偶函数定义的说明:
例题1 判断下列函数的奇偶性:
奇函数
偶函数
偶函数
非奇非偶函数
既奇又偶函数
判断函数奇偶性——定义法
典题讲解
(1) 先求定义域,看是否关于原点对称;
(2) 再判断 f(-x)=-f(x)或f(-x)=f(x)是否恒成立.
判断方法:①求f(-x)与f(x)比较
②求f(-x)+f(x)=0?或f(-x)-f(x)=0?
③求 或
用定义判断函数奇偶性的步骤:
方法总结
不关于原点对称即为非奇非偶函数。
奇函数
偶函数
奇函数
既奇又偶函数
非奇非偶函数
非奇非偶函数
练习1 判断下列函数的奇偶性:
例题2 判断下列函数的奇偶性.
解
函数奇偶性的判定的三种常用方法:
方法总结
定义法
图象法
性质法
(1)奇+奇=奇,奇-奇=奇,奇×奇=偶,奇÷奇=偶
(2)偶+偶=偶,偶-偶=偶,偶×偶=偶,偶÷偶=偶
(3)奇×偶=奇,奇÷偶=奇
利用奇偶性求函数的函数值
例题3 已知g(x)为奇函数,f(x)=g(x)+9,f(-2)=3,则f(2)=_______.
变式 已知f(x)=ax5-3bx3+2x+9,f(-2)=3,则f(2)=_______.
利用奇偶性求参数的值
2
利用奇偶性求函数的解析式
(2)已知函数 的图象关于原点对称,且当 时,
试求 在R上的解析式.
例题5(1)已知函数 的图象关于y轴对称,且当 时,
,试求 在R上的解析式.
(1)在哪个区间求解析式,x就设在哪个区间内;
(2)将-x代入已知区间的解析式;
(3)利用f(x)的奇偶性把 f(-x)变形成 -f(x)或f(x),从而解出f(x).
方法
总结
例题6 设函数 是奇函数, 是偶函数,且
试求 的解析式。
奇偶函数图象的性质
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
判断函数的奇偶性,简化函数图象的画法
例题6
奇偶函数图象的性质
书本P85 练习1
(1)若 为奇函数,在 上单调递增,则 在 上__________
函数的奇偶性与单调性的关系
奇函数在关于原点对称的区间上的单调性_____,
偶函数在关于原点对称的区间上的单调性_____
(填“相同”、“相反”).
相同
相反
(2)若 为偶函数,在 上单调递增,则 在 上__________
例题7
奇同偶异
练习1 定义在R上的偶函数f(x)在(0,+∞)上是增函数,则f(-π),f(3),f(-4)按从小到大的顺序排列是_________.
练习2 已知f(x)是定义在 上的奇函数,当x>0时,f(x)的图象如图所示,那么f(x)的值域是_____.
练习3 若 是定义在R上的奇函数,在 上为减函数,
且
(1)则 的解集为__________
(2)求 的解集为___________
练习4 若 是定义在R上的偶函数,在 上为减函数,
若 求x的取值范围
练习5 若奇函数 是定义在(-3,3)上的增函数,若
求实数m的取值范围.
1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
课堂小结
——第一课时
2020.10.22
图1
图2
图3
图4
新课导入
问题1 轴对称图形与中心对称图形的实质是什么?
轴对称图形 平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
中心对称图形 在平面内,把一个图形绕着某个点旋转180°,旋转后的图形能与原来的图形重合。
图1
图2
图3
图4
新课导入
问题2 观察下列函数图象,能否从对称的角度对下列函数进行分类?
我们将函数关于直角坐标系的对称的这种性质叫做函数的奇偶性,函数图像关于y轴对称的函数称作偶函数,函数图像关于坐标原点对称的函数称作奇函数。
问题3 函数 是否具有奇偶性?如果有奇偶性,是奇函数还是偶函数?
问题4 如何用数量关系刻画函数的奇偶性?
新课导入
观察下图,思考并讨论以下问题:
(1) 这两个偶函数图象有什么共同特征吗?
(2) 相应的两个函数值对应表是如何体现这些特征的?
x
-3
-2
-1
0
1
2
3
f(x)
x
-3
-2
-1
0
1
2
3
g(x)
9
4
1
0
1
4
9
1
3
2
0
1
2
3
新课讲授
知识探究(一)——偶函数
f(x)=x2
g(x)=|x|
偶函数的图象都关于y轴对称
(3) 什么是偶函数?
f(x)=x2
g(x)=|x|
定义
思考?函数f(x)=x2 , x∈[-1,2]是偶函数吗?偶函数的定义域有什么特征?
定义域关于原点对称
(1)两个奇函数图象有什么共同特征吗?
函数的图象都关于原点对称
(2)相应的两个函数值对应表是如何体现这些特征的?
x
-3
-2
-1
0
1
2
3
f(x)
x
-3
-2
-1
0
1
2
3
g(x)
-3
-2
-1
0
1
2
3
知识探究(二)——奇函数
观察下图,思考并讨论以下问题:
(3) 什么是奇函数?
定义
思考?设函数 是奇函数,且在 处有定义,则
思考?函数f(x)=x , x∈[-1,2]是奇函数吗?奇函数的定义域有什么特征?
定义域关于原点对称
函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则有f(-x)=-f(x)成立.
若f(x)为偶函数,则有f(-x)=f(x)成立.
对奇函数、偶函数定义的说明:
例题1 判断下列函数的奇偶性:
奇函数
偶函数
偶函数
非奇非偶函数
既奇又偶函数
判断函数奇偶性——定义法
典题讲解
(1) 先求定义域,看是否关于原点对称;
(2) 再判断 f(-x)=-f(x)或f(-x)=f(x)是否恒成立.
判断方法:①求f(-x)与f(x)比较
②求f(-x)+f(x)=0?或f(-x)-f(x)=0?
③求 或
用定义判断函数奇偶性的步骤:
方法总结
不关于原点对称即为非奇非偶函数。
奇函数
偶函数
奇函数
既奇又偶函数
非奇非偶函数
非奇非偶函数
练习1 判断下列函数的奇偶性:
例题2 判断下列函数的奇偶性.
解
函数奇偶性的判定的三种常用方法:
方法总结
定义法
图象法
性质法
(1)奇+奇=奇,奇-奇=奇,奇×奇=偶,奇÷奇=偶
(2)偶+偶=偶,偶-偶=偶,偶×偶=偶,偶÷偶=偶
(3)奇×偶=奇,奇÷偶=奇
利用奇偶性求函数的函数值
例题3 已知g(x)为奇函数,f(x)=g(x)+9,f(-2)=3,则f(2)=_______.
变式 已知f(x)=ax5-3bx3+2x+9,f(-2)=3,则f(2)=_______.
利用奇偶性求参数的值
2
利用奇偶性求函数的解析式
(2)已知函数 的图象关于原点对称,且当 时,
试求 在R上的解析式.
例题5(1)已知函数 的图象关于y轴对称,且当 时,
,试求 在R上的解析式.
(1)在哪个区间求解析式,x就设在哪个区间内;
(2)将-x代入已知区间的解析式;
(3)利用f(x)的奇偶性把 f(-x)变形成 -f(x)或f(x),从而解出f(x).
方法
总结
例题6 设函数 是奇函数, 是偶函数,且
试求 的解析式。
奇偶函数图象的性质
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
判断函数的奇偶性,简化函数图象的画法
例题6
奇偶函数图象的性质
书本P85 练习1
(1)若 为奇函数,在 上单调递增,则 在 上__________
函数的奇偶性与单调性的关系
奇函数在关于原点对称的区间上的单调性_____,
偶函数在关于原点对称的区间上的单调性_____
(填“相同”、“相反”).
相同
相反
(2)若 为偶函数,在 上单调递增,则 在 上__________
例题7
奇同偶异
练习1 定义在R上的偶函数f(x)在(0,+∞)上是增函数,则f(-π),f(3),f(-4)按从小到大的顺序排列是_________.
练习2 已知f(x)是定义在 上的奇函数,当x>0时,f(x)的图象如图所示,那么f(x)的值域是_____.
练习3 若 是定义在R上的奇函数,在 上为减函数,
且
(1)则 的解集为__________
(2)求 的解集为___________
练习4 若 是定义在R上的偶函数,在 上为减函数,
若 求x的取值范围
练习5 若奇函数 是定义在(-3,3)上的增函数,若
求实数m的取值范围.
1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数
2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
