1.4.1二次函数(第二课时)课件-2021-2022学年高一上学期数学北师大版(2019)必修第一册第一章(29张PPT)
文档属性
| 名称 | 1.4.1二次函数(第二课时)课件-2021-2022学年高一上学期数学北师大版(2019)必修第一册第一章(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 11:34:04 | ||
图片预览








文档简介
4.1一元二次函数
第二课时
制作老师:胡琪
§4 一元二次函数与一元二次不等式
教学目标
01
02
理解并掌握用二次函数的图像研究值域
利用图像直观判断与分析二次函数值的变化趋势
二次函数值域问题
重点
难点
含参区间上的二次函数值域问题
环节一
二次函数值的变化趋势
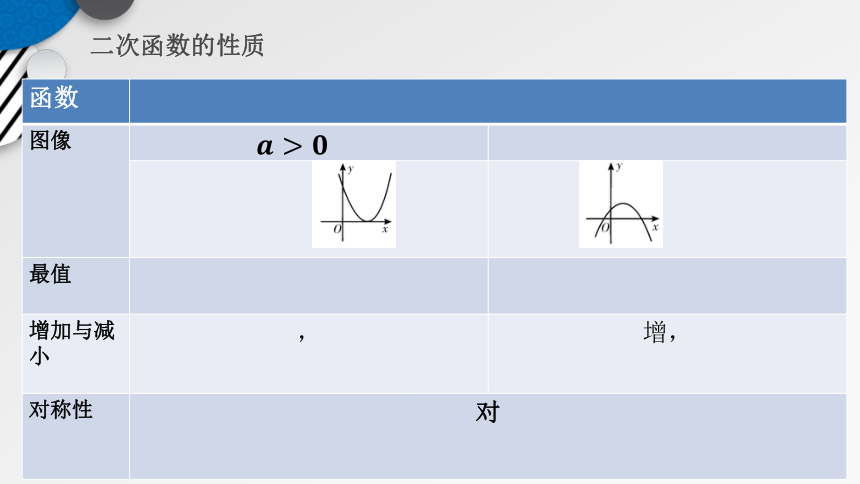
二次函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
????=????????????+????????+????????≠????
图像
????<0
最值
????????????????=?????????????????????????????
????????????????=?????????????????????????????
增加与减小
?∞,?????2????减,?????2????,+∞增
?∞,?????2????增,?????2????,+∞减
对称性
对称轴????=?????????????
????>????
?
解题指导
一元二次函数y=ax2+bx+c(a≠0) 函数值的变化趋势
(1)当a>0时,在区间 ?∞,????????????? 上,y随x的增大而减小;在区间 ?????????????,+∞上,y随x的增大而增大;简记:左减右增;
(2)当a<0时,在区间?∞,?????????????上,y随x的增大而增大;在区间 ?????????????,+∞上,y随x的增大而减小;简记:左增右减.
?
角度一
定义域是R
试述一元二次函数y=3x2-6x-1函数值的变化趋势
思路
配方成????=?????????????????+????,结合图像观察
?
解:????=??????????????????????,抛物线开口向上,对称轴????=????,在区间上????,+∞,y随x增大而增大;在区间?∞,????上,y随x增大而减小
?
微练
一元二次函数y=-x2+(m-1)x+m的图象与y轴交于(0,7)点.
试述函数值的变化趋势.
思路
求出????,配方成????=?????????????????+????,结合图像观察
?
因为y=-x2+(m-1)x+m的图象与y轴交于(0,7)点,得7=-0+(m-1)×0+m,所以m=7;则y=-x2+6x+7, 因为y=-x2+6x+7=-(x-3)2+16,所以对称轴为直线x=3,所以在区间
?∞,????上,y随x的增大而增大;在区间 ????,+∞ 上,y随x的增大而减小.
?
角度二
定义域是区间
试述一元二次函数y=3x2-6x-1,????∈?????,????上?函数值的变化趋势
?
思路
配方成????=?????????????????+????,结合图像和区间观察
?
解:????=??????????????????????,抛物线开口向上,对称轴????=????,且定义域是?????,????,所以,在区间上????,????,y随x增大而增大;在区间?????,????上,y随x增大而减小
?
-2
X=1
3
x
o
微练
试述一元二次函数y=3x2-6x-1,????∈?????,?????上?函数值的变化趋势
?
思路
配方成????=?????????????????+????,结合图像和区间观察
?
解:????=??????????????????????,抛物线开口向上,对称轴????=????,且定义域是?????,?????,所以,在区间?????,?????上,y随x增大而减小。
?
-2
X=1
3
x
o
-1
角度三
在区间(2,+∞)上,函数y=x2-mx+5的函数值y随x的增大而增大,则m的取值范围为 ( )
A.[4,+∞) B.[2,+∞)C.(-∞,4] D.(-∞,2]
思路
配方成????=?????????????????+????,结合图像(可以画简图,体现开口方向和对称轴)和区间观察
?
????=????????
?
逆向求参
y随x的增大而增大全部区间是????????,+∞
?
依题意(2,+∞)? ????????,+∞
?
????????≤????,????≤????
?
微练
若函数y=x2-2ax在区间(-∞,5]上y随x增大而减小,则实数a取值范围。
思路
配方成????=?????????????????+????,结合图像(可以画简图,体现开口方向和对称轴)和区间观察
?
????=????
?
y随x的增大而减小的全部区间?∞,????
?
依题意?∞,??????∞,????
?
所以,????≥????,????∈????,+∞
?
微练
若函数y=x2-2ax在区间(-∞,6]上y随x增大而减小,在[6,+∞)上y随x增大而增大,则实数a=
思路
配方成????=?????????????????+????,结合图像(可以画简图,体现开口方向和对称轴)和区间观察
?
????=????
?
由题知二次函数图象的对称轴为直线x=6.所以a=6.
环节二
二次函数的最值
求一元二次函数y=ax2+bx+c(a≠0)的最大(小)值的一般步骤
(1)“化”:采用配方法,化为y=a(x-h)2+k的形式;
(2)“求”:当a>0时,函数在x=h处y有最小值,ymin=k;当a<0时函数在x=h处y有最大值,ymax=k.
解题策略
提示
如果给定区间,要考虑区间与对称轴的位置关系,如果不确定,需分类讨论。
角度一
用配方法求出下列函数图象的对称轴及函数的最大值或最小值.
(1)y=2x2-4x-3;(2)y=-5x2-20x-26.
【解析】(1)配方得y=2x2-4x-3=2 ?????12?5,所以该函数图象开口向上,对称轴为直线x=1;当x=1取得最小值,最小值为ymin=-5;
?
定义域R
角度一
用配方法求出下列函数图象的对称轴及函数的最大值或最小值.
(1)y=2x2-4x-3;(2)y=-5x2-20x-26.
【解析】(2)配方得y=-5x2-20x-26=-5????+22-6,所以该函数图象开口向下,对称轴为直线x=-2;
当x=-2取得最大值,最大值为ymax=-6.
?
定义域R
角度二
若一元二次函数y=8x2-(m-1)x+m-7的最小值为0,则m=
【解析】由题意得即(m-1)2-4×8(m-7)=0.解得m=9或m=25.
答案:9或25
逆向求参
角度三
区间上最值问题
01
轴定区间定
03
轴动区间定
02
轴定区间动
04
轴动区间动
当 a >0时,它的图象是开口向上的抛物线,数形结合可得在 [m ,n]上 f (x) 的最值:
( 1 ) 当?????????????∈????,????时 , f ( x) 的 最 小 值 是????????????????????????????? ,最大值是f (m)、f (n) 中的较大者。
(2 )当?????????????≤????, 时,若,由 f ( x) 在 ????,????上是增加,则 f ( x) 的最小值是 f (m) ,最大值是 f (n)
(3)若?????????????≥????,由 f ( x) 在 ????,????上是减少,则 f ( x) 的最大值是 f (m) ,最小值是 f (n)
当a< 0 时,可类比得结论。
?
考向一
函数y =?????????+?????????????在区间[0 , 3] 上的最大值是_________,最小值是______
?
【解析】抛物线开口向下,对称轴是????=2,在区间内,如图
?
轴定区间定
最大值????????=????,最小值????????=?????
?
考向二
函数y =?????????????+????在区间[???? , ????+????] 上的最小值
?
【解析】抛物线开口向上,对称轴是????=1.
?
轴定区间动
????>????
?
????????????????????=????????=?????????????+????
?
????≤????≤????+????
?
????????????????????=????????=????
?
????+?????
????????????????????=????????+????=????????+????
?
f????????????????=?????????????+????,????>????????,????≤????≤????????????+????,?????
综合
分类讨论后,要记着总结成分段形式
考向三
函数y =????????+????????+????,????≥????,在区间[????? ????] 上的最值
?
【解析】抛物线开口向上,对称轴是????=?????2.因为????≥2,则?????2≤?1,如图。
?
轴动区间定
最小值?????????=?????????,最大值????????=????+????
?
由于限定了a,所以,没有出现分类讨论,控制了难度。实际考题中,可能包含分类讨论
考向四
函数y =??????????????????????+?????????????????????????,????>????,在区间????,+∞上的最小值
?
【解析】当3?2????≥????,0?
轴动区间动
当3?2????1,f????????????????=????????=?????32
?
????????????????????=?????????????????????????,????????
?
考向五
逆向求参
????????=??????????????????????+????????,知????????≤????????,????≤????????,????,??????∞,????,????????????????????=????????=????????,????????????????????=????????=????????,∴????=?????,????=????
?
已知函数????????=?????????????+????在区间????,????上最大值????????,最小值,????????求????,????值
?
单刀直入,避免了分类讨论。
环节三
小结
课堂小结
1.核心要点
应用 二次函数图像研究函数值变化趋势;
2.数学素养
1.通过图像研究培养想象力,数形结合能力;
2. 借助图像与性质应用,培养逻辑推理能力与素养
应用 二次函数图像研究函数最值;
谢谢观看
课件制作老师:胡琪
第二课时
制作老师:胡琪
§4 一元二次函数与一元二次不等式
教学目标
01
02
理解并掌握用二次函数的图像研究值域
利用图像直观判断与分析二次函数值的变化趋势
二次函数值域问题
重点
难点
含参区间上的二次函数值域问题
环节一
二次函数值的变化趋势
二次函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
????=????????????+????????+????????≠????
图像
????<0
最值
????????????????=?????????????????????????????
????????????????=?????????????????????????????
增加与减小
?∞,?????2????减,?????2????,+∞增
?∞,?????2????增,?????2????,+∞减
对称性
对称轴????=?????????????
????>????
?
解题指导
一元二次函数y=ax2+bx+c(a≠0) 函数值的变化趋势
(1)当a>0时,在区间 ?∞,????????????? 上,y随x的增大而减小;在区间 ?????????????,+∞上,y随x的增大而增大;简记:左减右增;
(2)当a<0时,在区间?∞,?????????????上,y随x的增大而增大;在区间 ?????????????,+∞上,y随x的增大而减小;简记:左增右减.
?
角度一
定义域是R
试述一元二次函数y=3x2-6x-1函数值的变化趋势
思路
配方成????=?????????????????+????,结合图像观察
?
解:????=??????????????????????,抛物线开口向上,对称轴????=????,在区间上????,+∞,y随x增大而增大;在区间?∞,????上,y随x增大而减小
?
微练
一元二次函数y=-x2+(m-1)x+m的图象与y轴交于(0,7)点.
试述函数值的变化趋势.
思路
求出????,配方成????=?????????????????+????,结合图像观察
?
因为y=-x2+(m-1)x+m的图象与y轴交于(0,7)点,得7=-0+(m-1)×0+m,所以m=7;则y=-x2+6x+7, 因为y=-x2+6x+7=-(x-3)2+16,所以对称轴为直线x=3,所以在区间
?∞,????上,y随x的增大而增大;在区间 ????,+∞ 上,y随x的增大而减小.
?
角度二
定义域是区间
试述一元二次函数y=3x2-6x-1,????∈?????,????上?函数值的变化趋势
?
思路
配方成????=?????????????????+????,结合图像和区间观察
?
解:????=??????????????????????,抛物线开口向上,对称轴????=????,且定义域是?????,????,所以,在区间上????,????,y随x增大而增大;在区间?????,????上,y随x增大而减小
?
-2
X=1
3
x
o
微练
试述一元二次函数y=3x2-6x-1,????∈?????,?????上?函数值的变化趋势
?
思路
配方成????=?????????????????+????,结合图像和区间观察
?
解:????=??????????????????????,抛物线开口向上,对称轴????=????,且定义域是?????,?????,所以,在区间?????,?????上,y随x增大而减小。
?
-2
X=1
3
x
o
-1
角度三
在区间(2,+∞)上,函数y=x2-mx+5的函数值y随x的增大而增大,则m的取值范围为 ( )
A.[4,+∞) B.[2,+∞)C.(-∞,4] D.(-∞,2]
思路
配方成????=?????????????????+????,结合图像(可以画简图,体现开口方向和对称轴)和区间观察
?
????=????????
?
逆向求参
y随x的增大而增大全部区间是????????,+∞
?
依题意(2,+∞)? ????????,+∞
?
????????≤????,????≤????
?
微练
若函数y=x2-2ax在区间(-∞,5]上y随x增大而减小,则实数a取值范围。
思路
配方成????=?????????????????+????,结合图像(可以画简图,体现开口方向和对称轴)和区间观察
?
????=????
?
y随x的增大而减小的全部区间?∞,????
?
依题意?∞,??????∞,????
?
所以,????≥????,????∈????,+∞
?
微练
若函数y=x2-2ax在区间(-∞,6]上y随x增大而减小,在[6,+∞)上y随x增大而增大,则实数a=
思路
配方成????=?????????????????+????,结合图像(可以画简图,体现开口方向和对称轴)和区间观察
?
????=????
?
由题知二次函数图象的对称轴为直线x=6.所以a=6.
环节二
二次函数的最值
求一元二次函数y=ax2+bx+c(a≠0)的最大(小)值的一般步骤
(1)“化”:采用配方法,化为y=a(x-h)2+k的形式;
(2)“求”:当a>0时,函数在x=h处y有最小值,ymin=k;当a<0时函数在x=h处y有最大值,ymax=k.
解题策略
提示
如果给定区间,要考虑区间与对称轴的位置关系,如果不确定,需分类讨论。
角度一
用配方法求出下列函数图象的对称轴及函数的最大值或最小值.
(1)y=2x2-4x-3;(2)y=-5x2-20x-26.
【解析】(1)配方得y=2x2-4x-3=2 ?????12?5,所以该函数图象开口向上,对称轴为直线x=1;当x=1取得最小值,最小值为ymin=-5;
?
定义域R
角度一
用配方法求出下列函数图象的对称轴及函数的最大值或最小值.
(1)y=2x2-4x-3;(2)y=-5x2-20x-26.
【解析】(2)配方得y=-5x2-20x-26=-5????+22-6,所以该函数图象开口向下,对称轴为直线x=-2;
当x=-2取得最大值,最大值为ymax=-6.
?
定义域R
角度二
若一元二次函数y=8x2-(m-1)x+m-7的最小值为0,则m=
【解析】由题意得即(m-1)2-4×8(m-7)=0.解得m=9或m=25.
答案:9或25
逆向求参
角度三
区间上最值问题
01
轴定区间定
03
轴动区间定
02
轴定区间动
04
轴动区间动
当 a >0时,它的图象是开口向上的抛物线,数形结合可得在 [m ,n]上 f (x) 的最值:
( 1 ) 当?????????????∈????,????时 , f ( x) 的 最 小 值 是????????????????????????????? ,最大值是f (m)、f (n) 中的较大者。
(2 )当?????????????≤????, 时,若,由 f ( x) 在 ????,????上是增加,则 f ( x) 的最小值是 f (m) ,最大值是 f (n)
(3)若?????????????≥????,由 f ( x) 在 ????,????上是减少,则 f ( x) 的最大值是 f (m) ,最小值是 f (n)
当a< 0 时,可类比得结论。
?
考向一
函数y =?????????+?????????????在区间[0 , 3] 上的最大值是_________,最小值是______
?
【解析】抛物线开口向下,对称轴是????=2,在区间内,如图
?
轴定区间定
最大值????????=????,最小值????????=?????
?
考向二
函数y =?????????????+????在区间[???? , ????+????] 上的最小值
?
【解析】抛物线开口向上,对称轴是????=1.
?
轴定区间动
????>????
?
????????????????????=????????=?????????????+????
?
????≤????≤????+????
?
????????????????????=????????=????
?
????+?????
????????????????????=????????+????=????????+????
?
f????????????????=?????????????+????,????>????????,????≤????≤????????????+????,?????
综合
分类讨论后,要记着总结成分段形式
考向三
函数y =????????+????????+????,????≥????,在区间[????? ????] 上的最值
?
【解析】抛物线开口向上,对称轴是????=?????2.因为????≥2,则?????2≤?1,如图。
?
轴动区间定
最小值?????????=?????????,最大值????????=????+????
?
由于限定了a,所以,没有出现分类讨论,控制了难度。实际考题中,可能包含分类讨论
考向四
函数y =??????????????????????+?????????????????????????,????>????,在区间????,+∞上的最小值
?
【解析】当3?2????≥????,0?
轴动区间动
当3?2????1,f????????????????=????????=?????32
?
????????????????????=?????????????????????????,????????
?
考向五
逆向求参
????????=??????????????????????+????????,知????????≤????????,????≤????????,????,??????∞,????,????????????????????=????????=????????,????????????????????=????????=????????,∴????=?????,????=????
?
已知函数????????=?????????????+????在区间????,????上最大值????????,最小值,????????求????,????值
?
单刀直入,避免了分类讨论。
环节三
小结
课堂小结
1.核心要点
应用 二次函数图像研究函数值变化趋势;
2.数学素养
1.通过图像研究培养想象力,数形结合能力;
2. 借助图像与性质应用,培养逻辑推理能力与素养
应用 二次函数图像研究函数最值;
谢谢观看
课件制作老师:胡琪
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
