3.3.2 抛物线的简单几何性质(第一课时)课件(共16张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.3.2 抛物线的简单几何性质(第一课时)课件(共16张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | ppt | ||
| 文件大小 | 407.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 14:33:59 | ||
图片预览



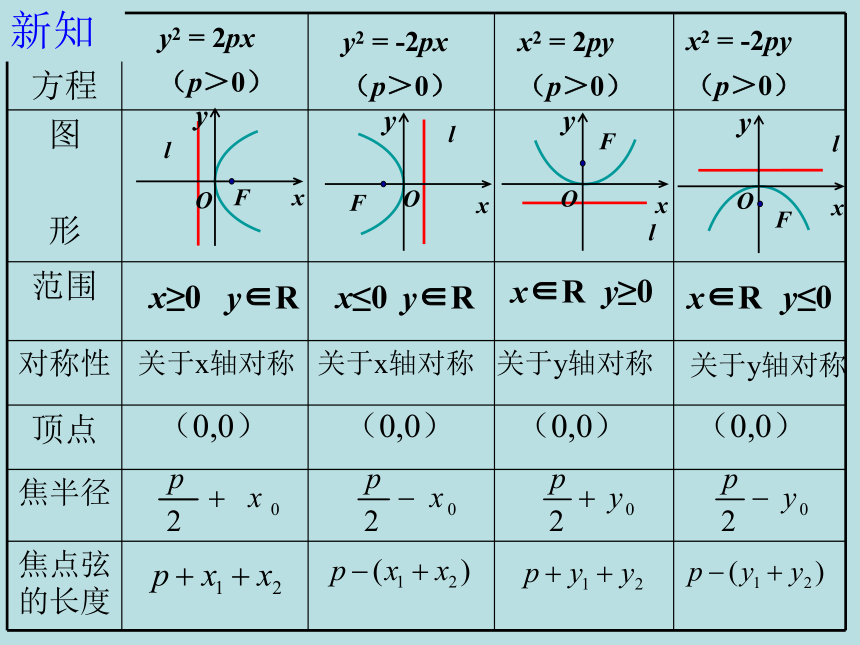


文档简介
(共16张PPT)
3.3.2抛物线的简单几何性质
第一课时
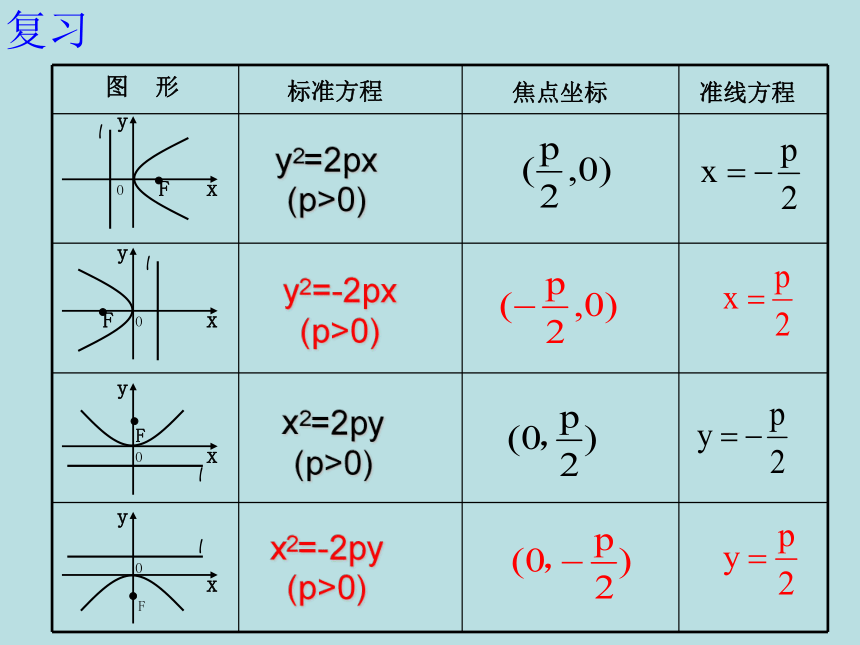
复习
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图
形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
引入
思考:类比椭圆、双曲线的几何性质,你认为应该研究抛物线y2
=
2px(p>0)的哪些几何性质?如何研究这些性质。
结合抛物线y2=2px(p>0)的标准方程和图形,探索其的几何性质:
(1)范围
(2)对称性
(3)顶点
(4)离心率
(5)焦半径
(6)通径
(7)焦点弦|PQ|:|PQ|=x1+x2+p
x≥0,y∈R
关于x轴对称,对称轴又叫抛物线的轴.
抛物线和它的轴的交点.
新知
x
O
y
F
P(x1,y1)
通过焦点且垂直对称轴的直线,与抛物线相交于两点,连接这两点的线段叫做抛物线的通径。
通径的长度:2P
|PF|=x1+
Q
(x2,y2)
e=1
方程
图
形
范围
对称性
顶点
焦半径
焦点弦的长度
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
(0,0)
(0,0)
(0,0)
(0,0)
新知
解:因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),
所以焦点F在x轴的正半轴
所以设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
例题
例3:已知抛物线关于x轴对称,它的顶点在坐标原
点,并且经过点M(2, ),求它的标准方程.
因为点M在抛物线上
所以
解:当焦点在x轴的正半轴时可设方程为:y2
=
2px(p>0)
所以p=2
因此所求抛物线标准方程为:y2
=
4x
当焦点在y轴的负半轴时可设方程为:x2
=
-2py(p>0)
因为点M在抛物线上
所以
因此所求抛物线标准方程为:
练习
思考:已知抛物线关于坐标轴对称,顶点在坐标原点,并且过点M(2,
),求它的标准方程.
(1)已知抛物线y2=8x,求出该抛物线的顶点、焦点、准线、对称轴、变量x的范围;
(2)抛物线的顶点在原点,对称轴重合于椭圆9x2+4y2=36短轴所在的直线,抛物线的焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.
练习
[解] (1)抛物线y2=8x,p=4,
所以顶点、焦点、准线、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.
(1)已知抛物线y2=8x,求出该抛物线的顶点、焦点、准线、对称轴、变量x的范围;
(2)抛物线的顶点在原点,对称轴重合于椭圆9x2+4y2=36短轴所在的直线,抛物线的焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.
练习
例4
斜率为1的直线
l经过抛物线y2
=
4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长。
例题
法二:设而不求,运用韦达定理,计算弦长
法一:直接求两点坐标,计算弦长
法三:设而不求,运用焦点弦公式,计算弦长
联立方程组
例题
x
y
O
F
A
B
B’
A’
解决过焦点的直线与抛物线相交的有关问题时,
注意将直线方程和抛物线方程联立得方程组,再结合根与系数的关系解题;注意焦点弦长、焦半径公式的应用,简化运算.
归纳
过点M(2,0)斜率为1的直线l,交抛物线y2=4x交于A、B两点,求|AB|
解:∵抛物线y2=4x
∴p=2,焦点为(1,0)
∵直线l的斜率为1且过点M(2,0)
∴直线l的方程为y=x-2
①
将①代入y2=4x得x2-8x+4=0
设A(x1,y1),B(x2,y2),则x1+x2=8,x1x2=4
所以
练习
已知A,B为抛物线E上不同的两点,若抛物线E的焦点为(1,0),线段AB恰被M(2,1)所平分.
(1)求抛物线E的方程;
(2)求直线AB的方程.
练习
方程
图
形
范围
对称性
顶点
焦半径
焦点弦的长度
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
(0,0)
(0,0)
(0,0)
(0,0)
小结
作业
课本
P138
练习
1、2
3.3.2抛物线的简单几何性质
第一课时
复习
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图
形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
引入
思考:类比椭圆、双曲线的几何性质,你认为应该研究抛物线y2
=
2px(p>0)的哪些几何性质?如何研究这些性质。
结合抛物线y2=2px(p>0)的标准方程和图形,探索其的几何性质:
(1)范围
(2)对称性
(3)顶点
(4)离心率
(5)焦半径
(6)通径
(7)焦点弦|PQ|:|PQ|=x1+x2+p
x≥0,y∈R
关于x轴对称,对称轴又叫抛物线的轴.
抛物线和它的轴的交点.
新知
x
O
y
F
P(x1,y1)
通过焦点且垂直对称轴的直线,与抛物线相交于两点,连接这两点的线段叫做抛物线的通径。
通径的长度:2P
|PF|=x1+
Q
(x2,y2)
e=1
方程
图
形
范围
对称性
顶点
焦半径
焦点弦的长度
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
(0,0)
(0,0)
(0,0)
(0,0)
新知
解:因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),
所以焦点F在x轴的正半轴
所以设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
例题
例3:已知抛物线关于x轴对称,它的顶点在坐标原
点,并且经过点M(2, ),求它的标准方程.
因为点M在抛物线上
所以
解:当焦点在x轴的正半轴时可设方程为:y2
=
2px(p>0)
所以p=2
因此所求抛物线标准方程为:y2
=
4x
当焦点在y轴的负半轴时可设方程为:x2
=
-2py(p>0)
因为点M在抛物线上
所以
因此所求抛物线标准方程为:
练习
思考:已知抛物线关于坐标轴对称,顶点在坐标原点,并且过点M(2,
),求它的标准方程.
(1)已知抛物线y2=8x,求出该抛物线的顶点、焦点、准线、对称轴、变量x的范围;
(2)抛物线的顶点在原点,对称轴重合于椭圆9x2+4y2=36短轴所在的直线,抛物线的焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.
练习
[解] (1)抛物线y2=8x,p=4,
所以顶点、焦点、准线、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.
(1)已知抛物线y2=8x,求出该抛物线的顶点、焦点、准线、对称轴、变量x的范围;
(2)抛物线的顶点在原点,对称轴重合于椭圆9x2+4y2=36短轴所在的直线,抛物线的焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.
练习
例4
斜率为1的直线
l经过抛物线y2
=
4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长。
例题
法二:设而不求,运用韦达定理,计算弦长
法一:直接求两点坐标,计算弦长
法三:设而不求,运用焦点弦公式,计算弦长
联立方程组
例题
x
y
O
F
A
B
B’
A’
解决过焦点的直线与抛物线相交的有关问题时,
注意将直线方程和抛物线方程联立得方程组,再结合根与系数的关系解题;注意焦点弦长、焦半径公式的应用,简化运算.
归纳
过点M(2,0)斜率为1的直线l,交抛物线y2=4x交于A、B两点,求|AB|
解:∵抛物线y2=4x
∴p=2,焦点为(1,0)
∵直线l的斜率为1且过点M(2,0)
∴直线l的方程为y=x-2
①
将①代入y2=4x得x2-8x+4=0
设A(x1,y1),B(x2,y2),则x1+x2=8,x1x2=4
所以
练习
已知A,B为抛物线E上不同的两点,若抛物线E的焦点为(1,0),线段AB恰被M(2,1)所平分.
(1)求抛物线E的方程;
(2)求直线AB的方程.
练习
方程
图
形
范围
对称性
顶点
焦半径
焦点弦的长度
y2
=
2px
(p>0)
y2
=
-2px
(p>0)
x2
=
2py
(p>0)
x2
=
-2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
(0,0)
(0,0)
(0,0)
(0,0)
小结
作业
课本
P138
练习
1、2
