3.3.1抛物线及其标准方程 课件(共18张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.3.1抛物线及其标准方程 课件(共18张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 537.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 14:33:19 | ||
图片预览


文档简介
3.3.1抛物线及其标准方程
关于x轴、y轴、原点对称
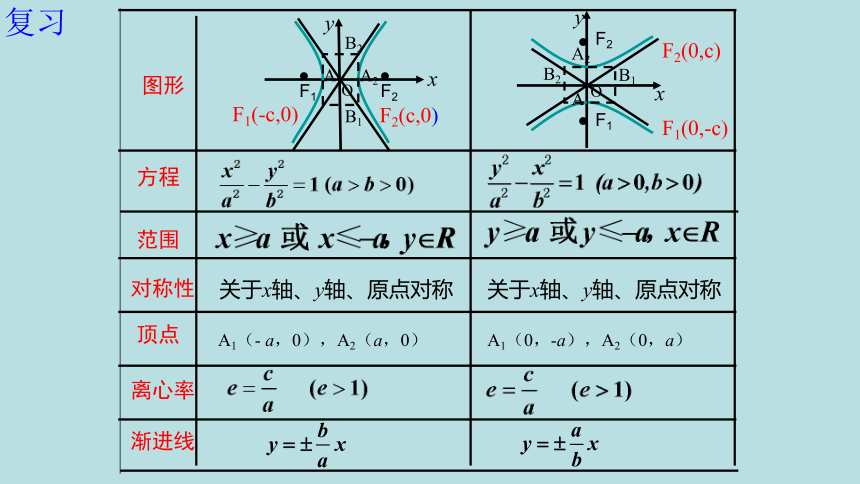
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
复习
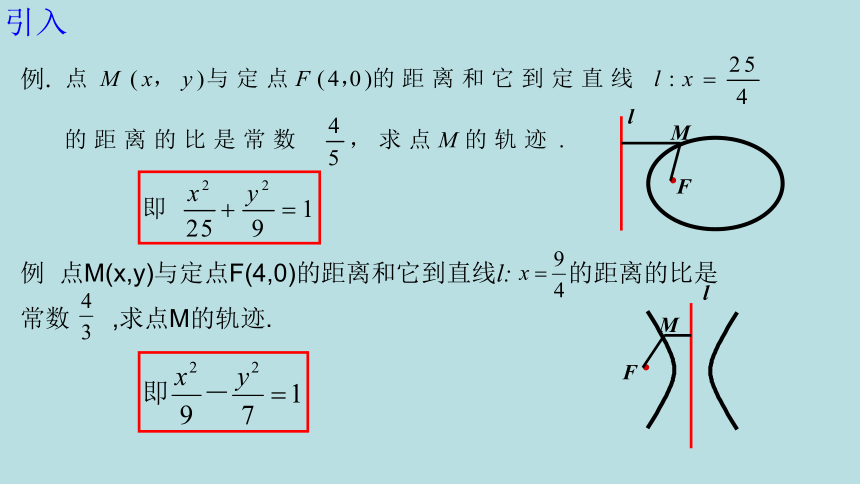
引入
例.
例 点M(x,y)与定点F(4,0)的距离和它到直线l: 的距离的比是常数 ,求点M的轨迹.
·
M
F
l
l
F
·
M
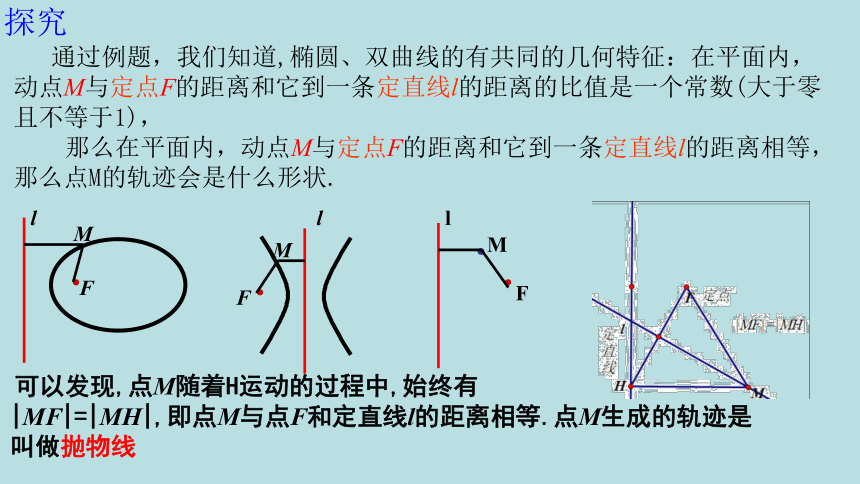
探究
通过例题,我们知道,椭圆、双曲线的有共同的几何特征:在平面内,动点M与定点F的距离和它到一条定直线l的距离的比值是一个常数(大于零且不等于1),
那么在平面内,动点M与定点F的距离和它到一条定直线l的距离相等,那么点M的轨迹会是什么形状.
·
M
F
l
l
F
·
M
·
F
M
l
·
可以发现,点M随着H运动的过程中,始终有
|MF|=|MH|,即点M与点F和定直线l的距离相等.点M生成的轨迹是叫做抛物线
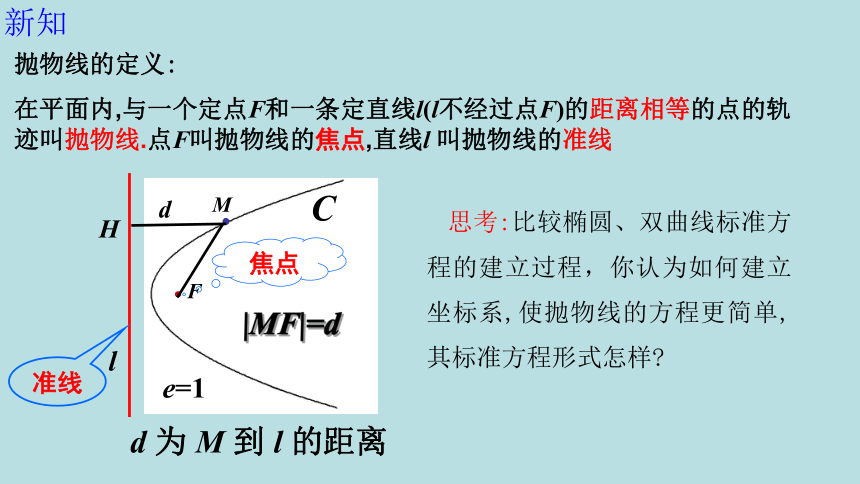
新知
抛物线的定义:
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,直线l 叫抛物线的准线
M
·
F
l
·
e=1
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
思考:比较椭圆、双曲线标准方程的建立过程,你认为如何建立坐标系,使抛物线的方程更简单,其标准方程形式怎样?
探究
标准方程的推导
l
x
K
y
o
M(x,y)
F
解:以过F且垂直于l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
设M(x,y),|FK|=p,则焦点F ,准线l为
依题意得
两边平方,整理得
表示焦点在x轴正半轴上,焦点坐标是 ,准线方程为
的抛物线的标准方程
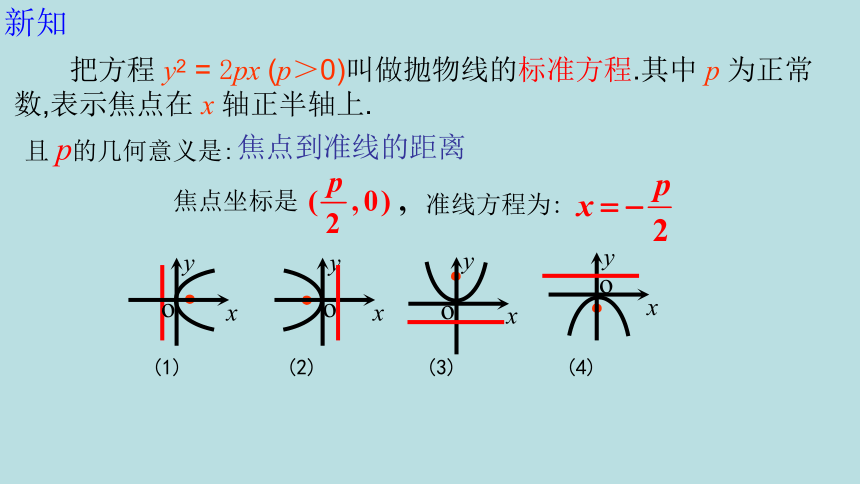
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数,表示焦点在 x 轴正半轴上.
且 p的几何意义是:
焦点坐标是
准线方程为:
﹒
y
x
o
(1)
﹒
y
x
o
﹒
y
x
o
(2)
(3)
﹒
y
x
o
(4)
焦点到准线的距离
新知
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离,
方程的特点:
(1)左边是二次式,
(2)右边是一次式;
四种抛物线的对比
相同点:
(1)顶点为原点;
(2)对称轴为坐标轴;
不同点:
(1)一次项变量为x(y),
则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
新知
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离,
方程的特点:
(1)左边是二次式,
(2)右边是一次式;
四种抛物线的对比
开口方向看正负
一次变量定焦点
焦准看p的一半
新知
焦点坐标
准线方程
(1)
(2)
(3)
(4)
(5,0)
x=-5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
练习
求下列抛物线的焦点坐标和准线方程
(1)y2 = 20x
(2)x2= y
(3)2y2 +5x =0
(4)x2 +8y =0
例1(1)已知抛物线的标准方程是y2 =6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
例题
解:(1)因为p=3,所以焦点坐标
准线方程是
(2)因为焦点在y轴的负半轴上,且
所以p=4,所以所求抛物线的标准方程是x2 =-8y
练习
根据下列条件,写出抛物线的标准方程
(1)焦点是F(3,0);
(2)准线方程 是x = ;
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =4x,y2 = -4x,x2 =4y 或 x2 = -4y
例2:一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的径口(直径)为4.8m,深度为0.5m。建立适当的坐标系,求抛物线的标准方程和焦点坐标。
x
y
O
A
B
例题
设抛物线的标准方程是y2=2px(p>0),由已知条件可得,点A的坐标是(0.5,2.4),代入方程,得
解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,
使接收天线的顶点(即抛物线的顶点)与原点重合。
即
所以,所求抛物线的标准方程是 ,焦点的坐标是
例题
求过点A(3,2)的抛物线的标准方程
x
y
o
(3,2)
解:当焦点在x轴的正半轴
设抛物线的标准方程是 y2 = 2px(p>0),因为A(3,2)在抛物线上
所以4=6p 解得p=
抛物线的标准方程为
当焦点在y轴的正半轴
设抛物线的标准方程是 x2 = 2py(p>0),因为A(3,2)在抛物线上
所以9=4p 解得p=
可得抛物线的标准方程为
y2 = x
4
3
x2 = y
9
2
2
3
9
4
练习
当焦点位置不确定时,结合图像,分类讨论进而写出抛物线的标准方程.
(1)抛物线y2 = 2px(p>0)上一点M到焦点的距离是a(a>0),则点M到准线的距离是 ,
点M的横坐标是 。
(2)抛物线y2 = 12x,上与焦点的距离
等于9的点的坐标是 。
F
l
H
·
·
y
x
K
O
M
a
a
练习
归纳:抛物线的定义及应用
抛物线的定义中指明了抛物线上的点到焦点的距离与到准线的距离相等,故二者可相互转化,这也是利用抛物线的定义解决最值问题及其他问题的实质.
小结
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
1.
开口方向看正负
一次变量定焦点
关键看p的一半
2.
作业
课本 P138 习题3.3 1、2
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
复习
引入
例.
例 点M(x,y)与定点F(4,0)的距离和它到直线l: 的距离的比是常数 ,求点M的轨迹.
·
M
F
l
l
F
·
M
探究
通过例题,我们知道,椭圆、双曲线的有共同的几何特征:在平面内,动点M与定点F的距离和它到一条定直线l的距离的比值是一个常数(大于零且不等于1),
那么在平面内,动点M与定点F的距离和它到一条定直线l的距离相等,那么点M的轨迹会是什么形状.
·
M
F
l
l
F
·
M
·
F
M
l
·
可以发现,点M随着H运动的过程中,始终有
|MF|=|MH|,即点M与点F和定直线l的距离相等.点M生成的轨迹是叫做抛物线
新知
抛物线的定义:
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,直线l 叫抛物线的准线
M
·
F
l
·
e=1
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
思考:比较椭圆、双曲线标准方程的建立过程,你认为如何建立坐标系,使抛物线的方程更简单,其标准方程形式怎样?
探究
标准方程的推导
l
x
K
y
o
M(x,y)
F
解:以过F且垂直于l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
设M(x,y),|FK|=p,则焦点F ,准线l为
依题意得
两边平方,整理得
表示焦点在x轴正半轴上,焦点坐标是 ,准线方程为
的抛物线的标准方程
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数,表示焦点在 x 轴正半轴上.
且 p的几何意义是:
焦点坐标是
准线方程为:
﹒
y
x
o
(1)
﹒
y
x
o
﹒
y
x
o
(2)
(3)
﹒
y
x
o
(4)
焦点到准线的距离
新知
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离,
方程的特点:
(1)左边是二次式,
(2)右边是一次式;
四种抛物线的对比
相同点:
(1)顶点为原点;
(2)对称轴为坐标轴;
不同点:
(1)一次项变量为x(y),
则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
新知
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离,
方程的特点:
(1)左边是二次式,
(2)右边是一次式;
四种抛物线的对比
开口方向看正负
一次变量定焦点
焦准看p的一半
新知
焦点坐标
准线方程
(1)
(2)
(3)
(4)
(5,0)
x=-5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
练习
求下列抛物线的焦点坐标和准线方程
(1)y2 = 20x
(2)x2= y
(3)2y2 +5x =0
(4)x2 +8y =0
例1(1)已知抛物线的标准方程是y2 =6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
例题
解:(1)因为p=3,所以焦点坐标
准线方程是
(2)因为焦点在y轴的负半轴上,且
所以p=4,所以所求抛物线的标准方程是x2 =-8y
练习
根据下列条件,写出抛物线的标准方程
(1)焦点是F(3,0);
(2)准线方程 是x = ;
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =4x,y2 = -4x,x2 =4y 或 x2 = -4y
例2:一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的径口(直径)为4.8m,深度为0.5m。建立适当的坐标系,求抛物线的标准方程和焦点坐标。
x
y
O
A
B
例题
设抛物线的标准方程是y2=2px(p>0),由已知条件可得,点A的坐标是(0.5,2.4),代入方程,得
解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,
使接收天线的顶点(即抛物线的顶点)与原点重合。
即
所以,所求抛物线的标准方程是 ,焦点的坐标是
例题
求过点A(3,2)的抛物线的标准方程
x
y
o
(3,2)
解:当焦点在x轴的正半轴
设抛物线的标准方程是 y2 = 2px(p>0),因为A(3,2)在抛物线上
所以4=6p 解得p=
抛物线的标准方程为
当焦点在y轴的正半轴
设抛物线的标准方程是 x2 = 2py(p>0),因为A(3,2)在抛物线上
所以9=4p 解得p=
可得抛物线的标准方程为
y2 = x
4
3
x2 = y
9
2
2
3
9
4
练习
当焦点位置不确定时,结合图像,分类讨论进而写出抛物线的标准方程.
(1)抛物线y2 = 2px(p>0)上一点M到焦点的距离是a(a>0),则点M到准线的距离是 ,
点M的横坐标是 。
(2)抛物线y2 = 12x,上与焦点的距离
等于9的点的坐标是 。
F
l
H
·
·
y
x
K
O
M
a
a
练习
归纳:抛物线的定义及应用
抛物线的定义中指明了抛物线上的点到焦点的距离与到准线的距离相等,故二者可相互转化,这也是利用抛物线的定义解决最值问题及其他问题的实质.
小结
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
1.
开口方向看正负
一次变量定焦点
关键看p的一半
2.
作业
课本 P138 习题3.3 1、2
