专题4 三角恒等变换同步专题集训- 2021-2022学年高一上学期数学(人教A版2019必修第一册)Word含解析
文档属性
| 名称 | 专题4 三角恒等变换同步专题集训- 2021-2022学年高一上学期数学(人教A版2019必修第一册)Word含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 507.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 14:51:31 | ||
图片预览




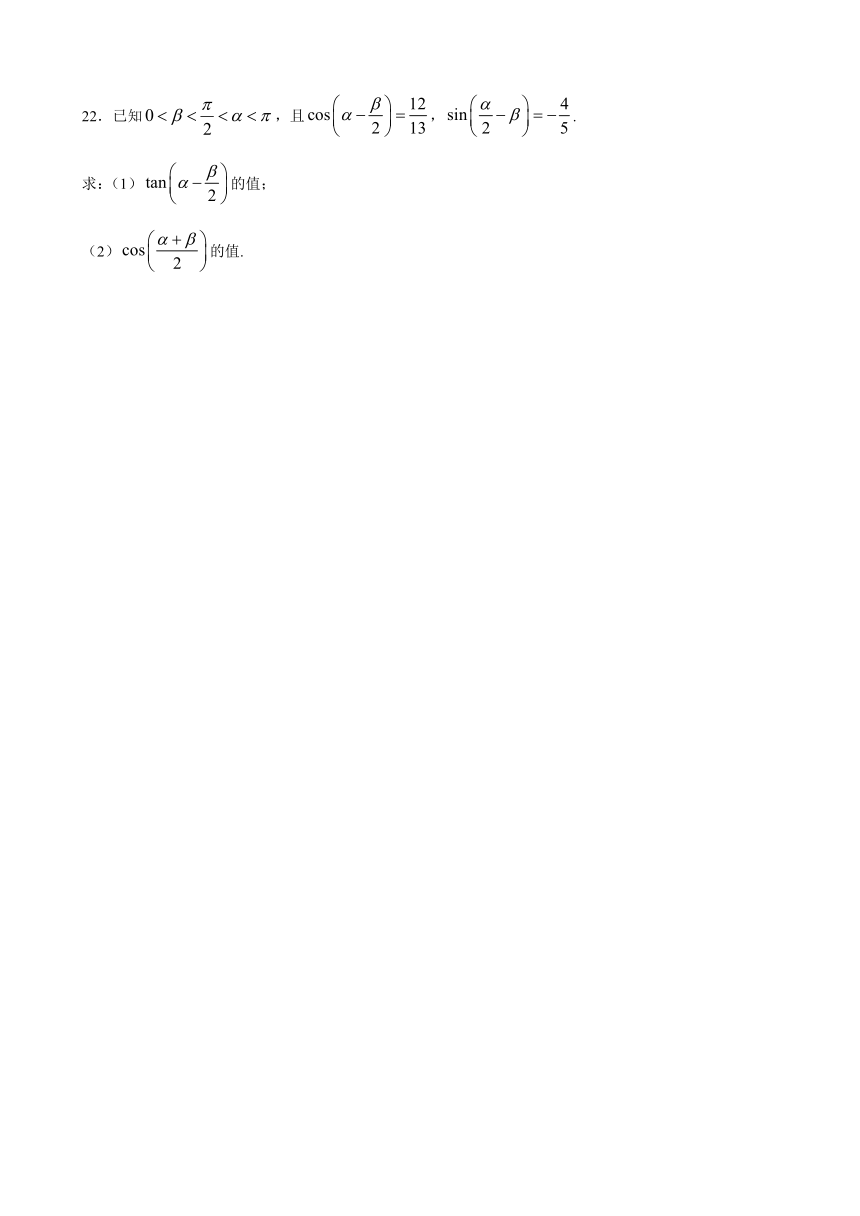
文档简介
2021-2022学年高一数学三角函数同步专题集训(人教A版2019必修第一册)专题4
三角恒等变换
一、单选题(本大题共8小题,每小题只有一个选项符合题意)
1.在中,,,则的值为(
)
A.
B.
C.
D.
2.函数是(
)
A.周期为的奇函数
B.周期为的偶函数
C.周期为的奇函数
D.周期为的偶函数
3.黄金分割比是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,该比值为,这是公认的最能引起美感的比例.我国著名数学家华罗庚以此引入并优化了现如今广泛应用于国内各个领域的“0.618优选法”.黄金分割比,它还可以近似表示为,则的值近似等于(
)
A.
B.1
C.2
D.
4.已知角α的终边经过点(-3,4),则sin的值为(
)
A.
B.-
C.
D.-
5.已知cos=,x∈(0,π),则sin
x的值为(
)
A.
B.
C.
D.
6.化简的结果为(
)
A.tan
B.
C.tan
α
D.
7.(
)
A.
B.
C.
D.4
8.若角,均为锐角,,,则(
)
A.
B.
C.或
D.
二、多选题(本大题共4小题,每小题有两项或以上符合题意)
9.若∈[0,2π],sinsincoscos0,则的值是(
)
A.
B.
C.
D.
10.下列四个等式,其中正确的是( )
A.tan25°+tan35°tan
25°tan35°
B.
C.cos2sin2
D.4
11.下列各式与tanα相等的是( )
A.
B.
C.
D.
12.已知,则等于( )
A.
B.
C.
D.
三、填空题(本大题共4小题)
13.若cos
αcos
β+sin
αsin
β=0,则α-β的值为________.
14.《周髀算经》中给出了弦图,所谓弦图(如图)是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形的两锐角分别为,,且小正方形与大正方形的面积之比为,则的值为___________.
15.已知锐角α,β满足sin
α=,cos
β=,则α+β=_____.
16.计算:____________.
四、解答题(本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程)
17.已知,
(1)判断的奇偶性;
(2)当时,画出的简图.
18.已知?为锐角,,.
(1)求的值;
(2)求的值.
19.已知矩形内接于半径为1的圆.
(1)求矩形面积的最大值;
(2)当矩形的面积最大时,矩形的周长也最大吗?说明理由.
20.已知函数
(1)作出在上的图像;
(2)若,判断是否为周期函数?如果是,求出最小正周期.
21.已知cosα,sin(α﹣β),且α、β∈(0,).求:
(Ⅰ)cos(2α﹣β)的值;
(Ⅱ)β的值.
22.已知,且,.
求:(1)的值;
(2)的值.
参考答案
1.B
【解析】由题得
所以,
所以.
故选:B
2.A
【解析】由题意得,
所以,故为奇函数,
周期,
故选:A
3.B
【解析】本题考查两角差的正弦公式、诱导公式.
由题意得,
故选:B.
4.C
【解析】解:设角的终边经过点,,
由三角函数的定义知:,,
.
故选:C.
5.B
【解析】由,所以,又,得,
所以
故选:B.
6.B
【解析】原式
=.
故选:B
7.C
【解析】;
故选:C
8.A
【解析】,均为锐角,,,
,,
.
故选:A.
9.CD
【解析】解:因为∈[0,2π],sinsincoscoscos=0,
则或,
故选:CD.
10.ABD
【解析】解:对A:,故,故正确;
对B:,故,故正确;
对C:,故错误;
对D:,故正确.
故选:.
11.BD
【解析】对于A,,
对于B,tanα,
对于C,,
对于D,tanα.
故选:BD.
12.CD
【解析】解:由得.
所以当时,原式;当时,原式.
故选:CD.
13.
【解析】解:由cos
αcos
β+sin
αsin
β=0,得,
所以,
故答案为:
14.
【解析】设大正方形的边长为,由小正方形与大正方形的面积之比为,
得小正方形的边长为,
则①,②.
由图可得,,
①②可得
,
解得.
故答案为:
15.
【解析】因为锐角α,β满足sin
α=,cos
β=,
,,
,
为锐角,,.
故答案为:.
16.
【解析】原式.
故答案为:.
17.(1)奇函数;(2)图像见解析.
【解析】(1)由解析式可得,即,即,
,即,
所以的定义域关于原点对称,
又,
为奇函数;
(2),
当时,画出的简图如下:
18.(1);(2).
【解析】(1),
;
(2),为锐角,,
,,
,.
.
19.(1)2;(2)是最大,最大为,理由见解析.
【解析】(1)如图所示,
设,
在中,,
,,
矩形的面积是
,
当时,矩形的面积取得最大值.
(2)矩形的周长是
,
当时,矩形的周长取得最大值;
综上,时,矩形面积与周长同时取得最大值,
即当矩形的面积最大时,矩形的周长也最大
20.(1)图象答案见解析;(2)是,最小正周期.
【解析】(1),即时,,
,即时,,
所以,
时,,时,,在上的图像如图:
(2),是周期函数,
因正弦函数和余弦都是周期函数,最小正周期为,
则时,,
,,
时,,
,,
即,,
所以是周期函数,最小正周期为.
21.(Ⅰ);(Ⅱ).
【解析】(Ⅰ)∵,∴α﹣β∈(,),
∵,,
∴sinα,cos(α﹣β),
∴cos(2α﹣β)=cos[(α﹣β)+α]=cos(α﹣β)cosα﹣sin(α﹣β)sinα
,
(Ⅱ)由(Ⅰ)得,
cosβ=cos[α﹣(α﹣β)]=cosα
cos(α﹣β)+
sinα
sin(α﹣β)
,
又∵,∴β.
22.(1);(2)
【解析】解:(1)由得,,
∴
,
(2)
由得,
,
.
三角恒等变换
一、单选题(本大题共8小题,每小题只有一个选项符合题意)
1.在中,,,则的值为(
)
A.
B.
C.
D.
2.函数是(
)
A.周期为的奇函数
B.周期为的偶函数
C.周期为的奇函数
D.周期为的偶函数
3.黄金分割比是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,该比值为,这是公认的最能引起美感的比例.我国著名数学家华罗庚以此引入并优化了现如今广泛应用于国内各个领域的“0.618优选法”.黄金分割比,它还可以近似表示为,则的值近似等于(
)
A.
B.1
C.2
D.
4.已知角α的终边经过点(-3,4),则sin的值为(
)
A.
B.-
C.
D.-
5.已知cos=,x∈(0,π),则sin
x的值为(
)
A.
B.
C.
D.
6.化简的结果为(
)
A.tan
B.
C.tan
α
D.
7.(
)
A.
B.
C.
D.4
8.若角,均为锐角,,,则(
)
A.
B.
C.或
D.
二、多选题(本大题共4小题,每小题有两项或以上符合题意)
9.若∈[0,2π],sinsincoscos0,则的值是(
)
A.
B.
C.
D.
10.下列四个等式,其中正确的是( )
A.tan25°+tan35°tan
25°tan35°
B.
C.cos2sin2
D.4
11.下列各式与tanα相等的是( )
A.
B.
C.
D.
12.已知,则等于( )
A.
B.
C.
D.
三、填空题(本大题共4小题)
13.若cos
αcos
β+sin
αsin
β=0,则α-β的值为________.
14.《周髀算经》中给出了弦图,所谓弦图(如图)是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形的两锐角分别为,,且小正方形与大正方形的面积之比为,则的值为___________.
15.已知锐角α,β满足sin
α=,cos
β=,则α+β=_____.
16.计算:____________.
四、解答题(本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程)
17.已知,
(1)判断的奇偶性;
(2)当时,画出的简图.
18.已知?为锐角,,.
(1)求的值;
(2)求的值.
19.已知矩形内接于半径为1的圆.
(1)求矩形面积的最大值;
(2)当矩形的面积最大时,矩形的周长也最大吗?说明理由.
20.已知函数
(1)作出在上的图像;
(2)若,判断是否为周期函数?如果是,求出最小正周期.
21.已知cosα,sin(α﹣β),且α、β∈(0,).求:
(Ⅰ)cos(2α﹣β)的值;
(Ⅱ)β的值.
22.已知,且,.
求:(1)的值;
(2)的值.
参考答案
1.B
【解析】由题得
所以,
所以.
故选:B
2.A
【解析】由题意得,
所以,故为奇函数,
周期,
故选:A
3.B
【解析】本题考查两角差的正弦公式、诱导公式.
由题意得,
故选:B.
4.C
【解析】解:设角的终边经过点,,
由三角函数的定义知:,,
.
故选:C.
5.B
【解析】由,所以,又,得,
所以
故选:B.
6.B
【解析】原式
=.
故选:B
7.C
【解析】;
故选:C
8.A
【解析】,均为锐角,,,
,,
.
故选:A.
9.CD
【解析】解:因为∈[0,2π],sinsincoscoscos=0,
则或,
故选:CD.
10.ABD
【解析】解:对A:,故,故正确;
对B:,故,故正确;
对C:,故错误;
对D:,故正确.
故选:.
11.BD
【解析】对于A,,
对于B,tanα,
对于C,,
对于D,tanα.
故选:BD.
12.CD
【解析】解:由得.
所以当时,原式;当时,原式.
故选:CD.
13.
【解析】解:由cos
αcos
β+sin
αsin
β=0,得,
所以,
故答案为:
14.
【解析】设大正方形的边长为,由小正方形与大正方形的面积之比为,
得小正方形的边长为,
则①,②.
由图可得,,
①②可得
,
解得.
故答案为:
15.
【解析】因为锐角α,β满足sin
α=,cos
β=,
,,
,
为锐角,,.
故答案为:.
16.
【解析】原式.
故答案为:.
17.(1)奇函数;(2)图像见解析.
【解析】(1)由解析式可得,即,即,
,即,
所以的定义域关于原点对称,
又,
为奇函数;
(2),
当时,画出的简图如下:
18.(1);(2).
【解析】(1),
;
(2),为锐角,,
,,
,.
.
19.(1)2;(2)是最大,最大为,理由见解析.
【解析】(1)如图所示,
设,
在中,,
,,
矩形的面积是
,
当时,矩形的面积取得最大值.
(2)矩形的周长是
,
当时,矩形的周长取得最大值;
综上,时,矩形面积与周长同时取得最大值,
即当矩形的面积最大时,矩形的周长也最大
20.(1)图象答案见解析;(2)是,最小正周期.
【解析】(1),即时,,
,即时,,
所以,
时,,时,,在上的图像如图:
(2),是周期函数,
因正弦函数和余弦都是周期函数,最小正周期为,
则时,,
,,
时,,
,,
即,,
所以是周期函数,最小正周期为.
21.(Ⅰ);(Ⅱ).
【解析】(Ⅰ)∵,∴α﹣β∈(,),
∵,,
∴sinα,cos(α﹣β),
∴cos(2α﹣β)=cos[(α﹣β)+α]=cos(α﹣β)cosα﹣sin(α﹣β)sinα
,
(Ⅱ)由(Ⅰ)得,
cosβ=cos[α﹣(α﹣β)]=cosα
cos(α﹣β)+
sinα
sin(α﹣β)
,
又∵,∴β.
22.(1);(2)
【解析】解:(1)由得,,
∴
,
(2)
由得,
,
.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
