2021-2022学年 青岛版九年级数学上册1.1相似多边形 教案
文档属性
| 名称 | 2021-2022学年 青岛版九年级数学上册1.1相似多边形 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 15:48:57 | ||
图片预览

文档简介
教学设计
课题
§1.1相似多边形
课标分析
《课标》要求,通过具体实例认识图形的相似,了解相似多边形和相似比。
学情分析
学生在八年级(上)中已涉及全等图形,对全等图形的概念及性质已有所了解,为学习认识相似图形做好了铺垫。
教材分析
根据《课程标准》,本节课主要讲解相似多边形的概念、性质,以及相似图形的判断方法。本节课内容为后面学习认识相似三角形做了铺垫,也是相似三角形的性质学习的基础。
教学目标
1、借助生活中的实例理解相似形的概念。
2、能正确应用相似多边形的概念判定多边形相似。
3、会按照要求求出相似多边形的相似比。
教学重难点
教学重点:深刻理解和掌握相似多边形的对应点、对应角、对应边以及表示方法。
教学难点:找对应边及对应角;根据定义求线段长和角度。
教学准备
教师准备:多媒体课件、直角三角尺
学生准备:导学案
直尺
量角器。
课时安排
一课时
教学评价
针对目标一和二:
1、90%的学生能理解相似形的概念,并能通过例题的讲解掌握相似形的性质。
2、80%的学生能正确应用相似多边形的概念判定多边形相似。
针对目标三:
1、70%的学生能通过小组讨论得出全等形和相似形的关系,并能理解相似比的概念。
2、60%的学生能通过当堂达标测试理清知识点之间的关系,构建知识结构网。
教学活动设计
[来:(一)复习旧知
导入新课
图片展示
1.什么叫全等形?全等形的性质?
2.什么叫成比例?什么叫比例线段?
二、探究新知
知识点一:相似形的概念
相似形:形状相同的平面图形叫相似形。
全等形与相似形的关系___________________________
(2)下列图形中,能确定相似的有(
)
A.两个半径不相等的圆;
B.所有的等边三角形;
C.所有的等腰三角形;
D.所有的正方形;
E.所有的等腰梯形;
F.所有的正六边形。
总结:
________________________________________________
知识点二;相似多边形的概念
同桌合作探究:
1.
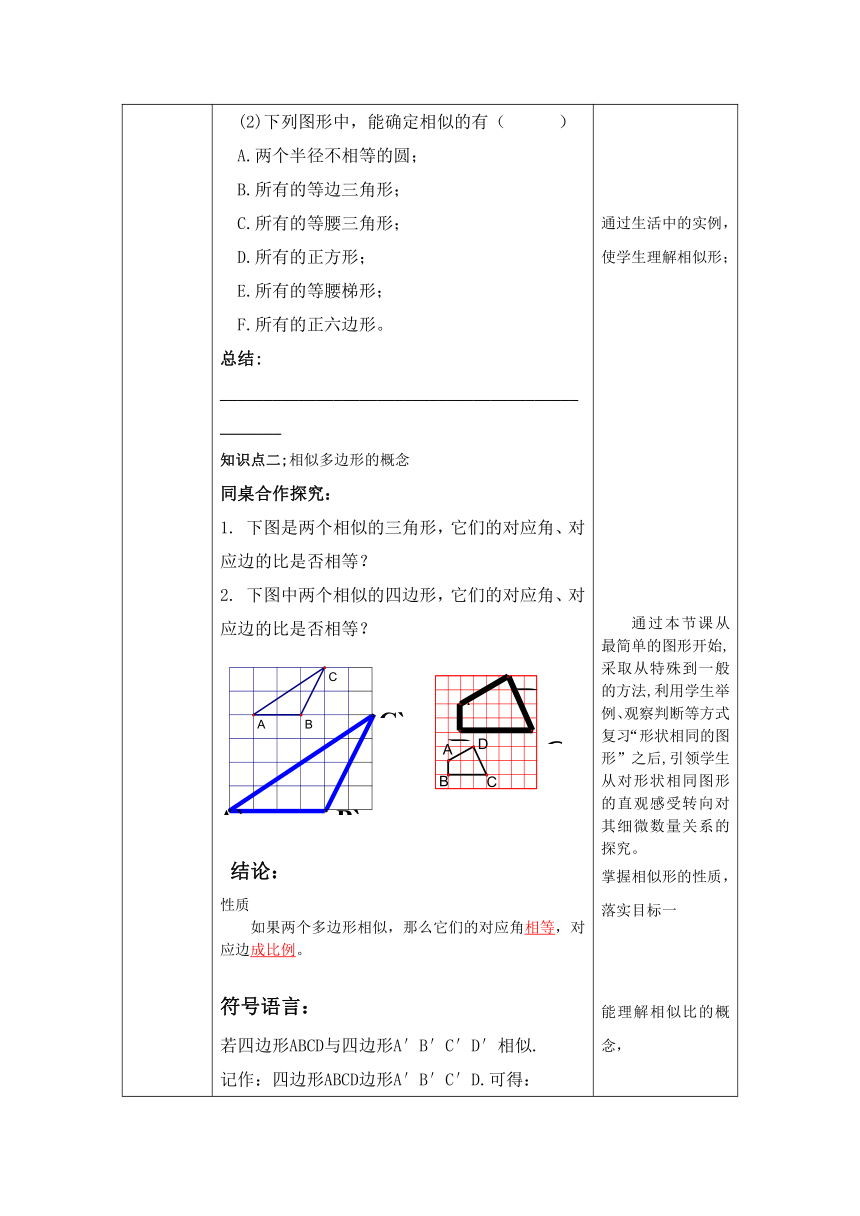
下图是两个相似的三角形,它们的对应角、对应边的比是否相等?
2.
下图中两个相似的四边形,它们的对应角、对应边的比是否相等?
结论:
性质
如果两个多边形相似,那么它们的对应角相等,对应边成比例。
符号语言:
若四边形ABCD与四边形A′B′C′D′相似.
记作:四边形ABCD边形A′B′C′D.可得:
;;;;
定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角相等,各边对应成比例,那么这两个多边形叫做相似多边形.
记法:——————————∽———————————.。
应注意什么?
2、议一议:
①观察下面两组图形,图中的两个图形相似吗?为什么?[]
?
②图中的两个图形相似吗?为什么?
相似比的概念:
相似多边形对应边的比叫做相似比.
4、精讲点拨:
【例1】
如图,四边形AEFD∽四边形EBCF.
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC
的长.
解:(1)∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,
∠DFE=∠C,∠D=∠EFC,
(2)∵AD=3,EF=4,代入得[]
,解得.
三、课堂小结
1、相似形的概念。
2、相似多边形的概念、表示方法,相似比的定义。
3、相似与全等的关系。
设计意图:
图片展示,通过创设情境,激发学生的学习兴趣。
通过小组讨论得出全等形和相似形的关系,
[]
通过生活中的实例,使学生理解相似形;
[]
[]
通过本节课从最简单的图形开始,
采取从特殊到一般的方法,利用学生举例、观察判断等方式复习“形状相同的图形”之后,引领学生从对形状相同图形的直观感受转向对其细微数量关系的探究。
掌握相似形的性质,落实目标一
能理解相似比的概念,
自主探究、合作学习是现代教学的主要形式,让学生在独立思考和合作交流中学习知识能加深对知识的理解.学生在交流中思维碰撞,能产生新的思维火花。
板书设计
§1.1相似多边形
相似形
例1、
性质
3、相似多边形
4、相似比
作业设计
(五)达标检测
1.下列说法中,错误的是(
)
A.等边三角形都相似
B.等腰直角三角形都相似
C.矩形都相似
D.正方形都相似
2.
手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边框,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是(
)
3.
判断:
(1)任意两个矩形都是相似图形(
)
(2)任意两个圆形是相似图形(
)
(3)对应角相等的两个四边形是相似多边形(
)
(4)两个正五边形是相似多边形(
)
(5)两个全等三角形是相似多边形(
)
(6)两菱形是相似多边形(
)
(7)两个相似多边形,对应边成比例(
)
4.如图所示的两个四边形相似则α的度数是(
)
A.87°??????????????B.60°???C.75°??????????????D.120°
一个三角形的三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为(
)
A.15???????????????B.10???????????????C.9?????????????D.3
课题
§1.1相似多边形
课标分析
《课标》要求,通过具体实例认识图形的相似,了解相似多边形和相似比。
学情分析
学生在八年级(上)中已涉及全等图形,对全等图形的概念及性质已有所了解,为学习认识相似图形做好了铺垫。
教材分析
根据《课程标准》,本节课主要讲解相似多边形的概念、性质,以及相似图形的判断方法。本节课内容为后面学习认识相似三角形做了铺垫,也是相似三角形的性质学习的基础。
教学目标
1、借助生活中的实例理解相似形的概念。
2、能正确应用相似多边形的概念判定多边形相似。
3、会按照要求求出相似多边形的相似比。
教学重难点
教学重点:深刻理解和掌握相似多边形的对应点、对应角、对应边以及表示方法。
教学难点:找对应边及对应角;根据定义求线段长和角度。
教学准备
教师准备:多媒体课件、直角三角尺
学生准备:导学案
直尺
量角器。
课时安排
一课时
教学评价
针对目标一和二:
1、90%的学生能理解相似形的概念,并能通过例题的讲解掌握相似形的性质。
2、80%的学生能正确应用相似多边形的概念判定多边形相似。
针对目标三:
1、70%的学生能通过小组讨论得出全等形和相似形的关系,并能理解相似比的概念。
2、60%的学生能通过当堂达标测试理清知识点之间的关系,构建知识结构网。
教学活动设计
[来:(一)复习旧知
导入新课
图片展示
1.什么叫全等形?全等形的性质?
2.什么叫成比例?什么叫比例线段?
二、探究新知
知识点一:相似形的概念
相似形:形状相同的平面图形叫相似形。
全等形与相似形的关系___________________________
(2)下列图形中,能确定相似的有(
)
A.两个半径不相等的圆;
B.所有的等边三角形;
C.所有的等腰三角形;
D.所有的正方形;
E.所有的等腰梯形;
F.所有的正六边形。
总结:
________________________________________________
知识点二;相似多边形的概念
同桌合作探究:
1.
下图是两个相似的三角形,它们的对应角、对应边的比是否相等?
2.
下图中两个相似的四边形,它们的对应角、对应边的比是否相等?
结论:
性质
如果两个多边形相似,那么它们的对应角相等,对应边成比例。
符号语言:
若四边形ABCD与四边形A′B′C′D′相似.
记作:四边形ABCD边形A′B′C′D.可得:
;;;;
定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角相等,各边对应成比例,那么这两个多边形叫做相似多边形.
记法:——————————∽———————————.。
应注意什么?
2、议一议:
①观察下面两组图形,图中的两个图形相似吗?为什么?[]
?
②图中的两个图形相似吗?为什么?
相似比的概念:
相似多边形对应边的比叫做相似比.
4、精讲点拨:
【例1】
如图,四边形AEFD∽四边形EBCF.
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC
的长.
解:(1)∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,
∠DFE=∠C,∠D=∠EFC,
(2)∵AD=3,EF=4,代入得[]
,解得.
三、课堂小结
1、相似形的概念。
2、相似多边形的概念、表示方法,相似比的定义。
3、相似与全等的关系。
设计意图:
图片展示,通过创设情境,激发学生的学习兴趣。
通过小组讨论得出全等形和相似形的关系,
[]
通过生活中的实例,使学生理解相似形;
[]
[]
通过本节课从最简单的图形开始,
采取从特殊到一般的方法,利用学生举例、观察判断等方式复习“形状相同的图形”之后,引领学生从对形状相同图形的直观感受转向对其细微数量关系的探究。
掌握相似形的性质,落实目标一
能理解相似比的概念,
自主探究、合作学习是现代教学的主要形式,让学生在独立思考和合作交流中学习知识能加深对知识的理解.学生在交流中思维碰撞,能产生新的思维火花。
板书设计
§1.1相似多边形
相似形
例1、
性质
3、相似多边形
4、相似比
作业设计
(五)达标检测
1.下列说法中,错误的是(
)
A.等边三角形都相似
B.等腰直角三角形都相似
C.矩形都相似
D.正方形都相似
2.
手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边框,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是(
)
3.
判断:
(1)任意两个矩形都是相似图形(
)
(2)任意两个圆形是相似图形(
)
(3)对应角相等的两个四边形是相似多边形(
)
(4)两个正五边形是相似多边形(
)
(5)两个全等三角形是相似多边形(
)
(6)两菱形是相似多边形(
)
(7)两个相似多边形,对应边成比例(
)
4.如图所示的两个四边形相似则α的度数是(
)
A.87°??????????????B.60°???C.75°??????????????D.120°
一个三角形的三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为(
)
A.15???????????????B.10???????????????C.9?????????????D.3
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
