2021—2022学年人教版七年级数学上册1.3.1有理数的加法-课件(17张PPT)
文档属性
| 名称 | 2021—2022学年人教版七年级数学上册1.3.1有理数的加法-课件(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 352.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 20:31:30 | ||
图片预览





文档简介
(共17张PPT)
1.3.1
有理数的加法
复习
?
任何一个有理数是由
这两部分组成的;
?
用“绝对值”与“符号”两个概念来定义“相反数”:
相等、
相反的两个有理数,叫做一对相反数;
符号(正、负号)、
绝对值
绝对值
符号
两个有理数进行加法运算时,这两个加数的符号可能有哪些情况呢?
利用数轴探索如何进行有理数的加法
一个物体作左右方向的运动,我们规定向右为正,向左为负。如向右运动5m记作5m,向左5m记作-5m.
探究一:
(1)
如果物体先向右运动5m,再向右运动3m,那么两次运动后总的结果是什么?
0
5
3
8
5+3=8
(2)
如果物体先向左运动5m,再向左运动3m,那么两次运动后总的结果是什么?
-5
-3
0
-
8
(-5)+(-3)=-
8
结论:同号两数相加,取相同的符号,
并把绝对值相加。
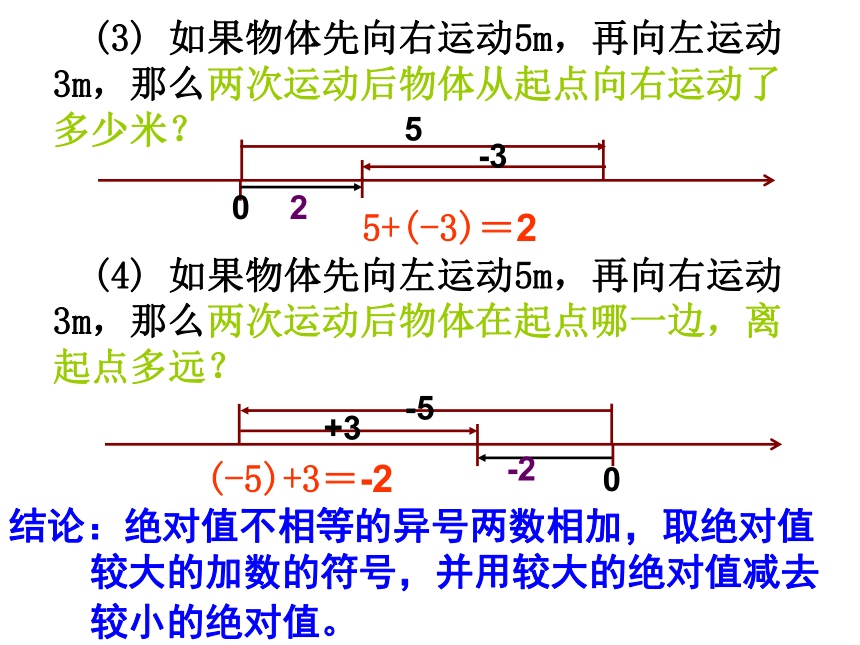
(3)
如果物体先向右运动5m,再向左运动3m,那么两次运动后物体从起点向右运动了多少米?
5+(-3)=2
5
-3
2
0
(4)
如果物体先向左运动5m,再向右运动3m,那么两次运动后物体在起点哪一边,离起点多远?
0
(-5)+3=-2
-5
+3
-2
结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
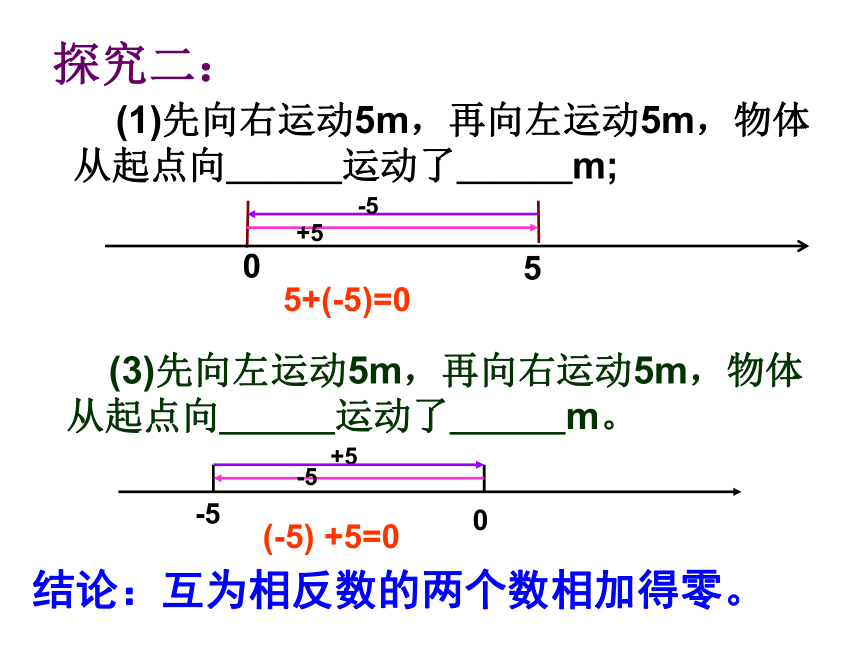
探究二:
(1)先向右运动5m,再向左运动5m,物体从起点向___运动了___m;
(3)先向左运动5m,再向右运动5m,物体从起点向___运动了___m。
0
5
+5
-5
5+(-5)=0
-5
0
-5
+5
(-5)
+5=0
结论:互为相反数的两个数相加得零。
探究三
(1)如果物体第1秒向右运动了5m,第2秒原地不动,两秒后物体从起点向右运动了多少米?
(2)如果物体第1秒向左运动了5m,第2秒原地不动,两秒后物体从起点向左运动了多少米?
5+0=5
(-5)+0=-5
结论:一个数同零相加,仍得这个数。
通过以上探索,你来观察一下,在两个有理数相加的过程中“和的符号”怎样确定?“和的绝对值”怎样确定?一个有理数同0相加,和是多少?
赶快动脑筋,说说自己的想法
有理数的加法法则
(1):同号两数相加,取相同的符号,并把绝对值相加。
(2):异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
(3):一个数同0相加,仍得这个数。
阅读下列解题过程,是否有错?若有错,请说出错的原因。
计算
(+3)+(-5)
解:(+3)+(-5)=2
正确解法:(+3)+(-5)
=-(5-3)
=-2
错解分析:本题计算忽略了“先定符号,后计算绝对值”的顺序,因此平时解题时,一定要遵循法则等
(异号两数相加)
(取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值)
计算下列各题:
(1)(-10)+(-1);
(2)180+(-10);
(3)5+(-5);
(4)0+(-2).
随堂练习
计算
(1)(-25)+(-7);
(2)(-13)+5;
(3)(-23)+0;
(4)
45+(-45).
1.两个数相加,和一定大于其中一个加数吗?
通过这节课的学习,你有什么收获或体会?给同伴说说。
思考
2.当三个或三个以上的有理数相加时,你会做吗?
作业:
书上19页第3题
要求:用数学式子表示出来,并算出结果
练习:计算:
(1)15+(-22);
(2)(-0.9)+1.5;
(3)2.7+(-3.5)
(4)
练习:
计算
(1)
(+3)+(+7)
(2)(-25)+(-7)
(3)(-6)+(-2)
1.3.1
有理数的加法
复习
?
任何一个有理数是由
这两部分组成的;
?
用“绝对值”与“符号”两个概念来定义“相反数”:
相等、
相反的两个有理数,叫做一对相反数;
符号(正、负号)、
绝对值
绝对值
符号
两个有理数进行加法运算时,这两个加数的符号可能有哪些情况呢?
利用数轴探索如何进行有理数的加法
一个物体作左右方向的运动,我们规定向右为正,向左为负。如向右运动5m记作5m,向左5m记作-5m.
探究一:
(1)
如果物体先向右运动5m,再向右运动3m,那么两次运动后总的结果是什么?
0
5
3
8
5+3=8
(2)
如果物体先向左运动5m,再向左运动3m,那么两次运动后总的结果是什么?
-5
-3
0
-
8
(-5)+(-3)=-
8
结论:同号两数相加,取相同的符号,
并把绝对值相加。
(3)
如果物体先向右运动5m,再向左运动3m,那么两次运动后物体从起点向右运动了多少米?
5+(-3)=2
5
-3
2
0
(4)
如果物体先向左运动5m,再向右运动3m,那么两次运动后物体在起点哪一边,离起点多远?
0
(-5)+3=-2
-5
+3
-2
结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
探究二:
(1)先向右运动5m,再向左运动5m,物体从起点向___运动了___m;
(3)先向左运动5m,再向右运动5m,物体从起点向___运动了___m。
0
5
+5
-5
5+(-5)=0
-5
0
-5
+5
(-5)
+5=0
结论:互为相反数的两个数相加得零。
探究三
(1)如果物体第1秒向右运动了5m,第2秒原地不动,两秒后物体从起点向右运动了多少米?
(2)如果物体第1秒向左运动了5m,第2秒原地不动,两秒后物体从起点向左运动了多少米?
5+0=5
(-5)+0=-5
结论:一个数同零相加,仍得这个数。
通过以上探索,你来观察一下,在两个有理数相加的过程中“和的符号”怎样确定?“和的绝对值”怎样确定?一个有理数同0相加,和是多少?
赶快动脑筋,说说自己的想法
有理数的加法法则
(1):同号两数相加,取相同的符号,并把绝对值相加。
(2):异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
(3):一个数同0相加,仍得这个数。
阅读下列解题过程,是否有错?若有错,请说出错的原因。
计算
(+3)+(-5)
解:(+3)+(-5)=2
正确解法:(+3)+(-5)
=-(5-3)
=-2
错解分析:本题计算忽略了“先定符号,后计算绝对值”的顺序,因此平时解题时,一定要遵循法则等
(异号两数相加)
(取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值)
计算下列各题:
(1)(-10)+(-1);
(2)180+(-10);
(3)5+(-5);
(4)0+(-2).
随堂练习
计算
(1)(-25)+(-7);
(2)(-13)+5;
(3)(-23)+0;
(4)
45+(-45).
1.两个数相加,和一定大于其中一个加数吗?
通过这节课的学习,你有什么收获或体会?给同伴说说。
思考
2.当三个或三个以上的有理数相加时,你会做吗?
作业:
书上19页第3题
要求:用数学式子表示出来,并算出结果
练习:计算:
(1)15+(-22);
(2)(-0.9)+1.5;
(3)2.7+(-3.5)
(4)
练习:
计算
(1)
(+3)+(+7)
(2)(-25)+(-7)
(3)(-6)+(-2)
