湘教版七年级上册数学 第2章 代数式2.1用字母表示数 课件(共30张PPT)
文档属性
| 名称 | 湘教版七年级上册数学 第2章 代数式2.1用字母表示数 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 19:31:22 | ||
图片预览










文档简介
(共30张PPT)
第1节
用字母表示数
第二章
代数式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
含字母式子的书写方法
用字母表示数量关系
用字母表示图形关系
课时导入
复习提问
引出问题
科学家爱因斯坦上小学时,在一次数学课中,发现了下列的等式:
1+2-2+1,
3.5+5.6=5.6+3.5,
他认为,这是数的运算的一个重要规律,于是就把这个规律告诉了他的老师和同学,得到了大家的赞赏.
知识点
含字母式子的书写方法
知1-导
感悟新知
1
据中国新闻网2011年9月19日报道:中国工程院院士袁隆平指导的“Y两优2号”百亩超级杂交稻试验田平均亩产926.6
kg,创中国大面积水稻亩产的最高纪录.
知1-导
感悟新知
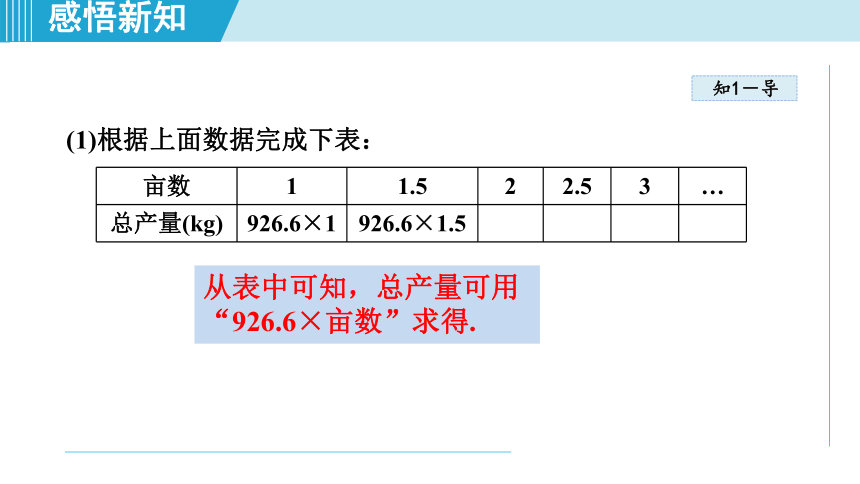
(1)根据上面数据完成下表:
亩数
1
1.5
2
2.5
3
…
总产量(kg)
926.6×1
926.6×1.5
从表中可知,总产量可用“926.6×亩数”求得.
知1-导
感悟新知
(2)如果用字母a表示亩数,那么a亩水稻的总产量是多少?
(3)如果平均亩产为b
kg,那么a亩水稻的总产量是多少?
a亩水稻的总产量是926.6×a(kg).
平均亩产为bkg时,a亩水稻的总产量是a×b(kg).
知1-导
感悟新知
2011年9月29日
21
时169,我国成功发射了“天官一号”飞行器,它是目前中国最大、最重的在轨飞行航天器.已知“天宫一号”大约每小时绕地球飞行2.844万千米,则它飞行2
h,25
h分别飞行了多少
万千米?如果时间为th,那么它飞
行了多少万千米?
知1-导
感悟新知
“天宫一号”飞行2h,2.5
h分别飞行了(2.844×2)万千米,(2.844×2.5)万千米.
th飞行了2.8441万千米
知1-讲
感悟新知
1.
意义:用表示数的字母表示问题中的数或数量关系;用字母表示数可以统一、简明地表示实际问题中的数量关系.
知1-讲
感悟新知
2.用字母表示数的书写规则:
(1)字母与字母相乘时,“×”通常省略不写或写成“.”;
(2)字母与数字相乘时,数字通常写在字母的前面;
(3)带分数与字母相乘时,通常化带分数为假分数;
(4)字母与字母相除时,要写成分数的形式。
(5)数字与数字相乘,一般仍用“×”号,也可用“.”号,但要注意与小数点分开.
知1-讲
感悟新知
3.易错警示:
(1)同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示;
(2)用字母表示实际问题中的某个量时,字母取值必须使式子有意义且符合实际情况.
知1-讲
感悟新知
例
1
填空:
(1)比a的0.6倍大c的数________;
(2)a与b的2倍的积为________.
0.6a+c
2ab
方法点拨
用字母表示日常生活中的数或数量关系,仅仅是把具体数用字母代替了,其实际意义与具体数是一致的,它将个别数量关系转变为一般数量关系.
知1-讲
总
结
感悟新知
列字母表达式的步骤:
(1)认真审题,将问题中表示数量关系的词语正确地转化为对应的运算;
(2)注意语言所表达的运算顺序,一般“先读先写";
(3)浓缩原题,分段处理,即在比较复杂的语句中,一般会有多个“的”字出现,列式时,可找出各个“的”字将句子分成几段,逐步列出.
知1-练
感悟新知
D
C
知2-导
感悟新知
知识点
用字母表示数量关系
2
①注意字母具有一般性:用字母可以表示我们已经学过的任意一个有理数,同时随着我们所学知识的深入与需要,数的范围将进一步扩大,字母可以表示今后我们所学到的任何一个数.
②注意字母的确定性,它表现在两个方面:一方面是指在同一个问题中,同一个字母只能表示同一个量,不同数量要用不同的字母来表示.另一方面,在用字母表示数时,一旦式子中的字母的取值确定了,式子的值也就随之确定了.
知2-导
感悟新知
③注意字母的不确定性:同一个式子可以表示多种实际问题中的数量关系.
④注意字母的限制性:用字母表示实际问题中的某一个数量时,字母的取值必须使这个问题有意义且符合实际.
⑤注意字母的抽象性:要逐步理解和接受有些问题的结果可能就是一个用字母表示的式子.
知2-导
感悟新知
⑥字母的选择:同一个数量可以用不同的字母表示,同一字母在不同的环境中可以表示不同的数,在同一题中不同的数要用不同的字母表示.
知2-导
感悟新知
例2
2小莉以5km/h的速度,走了20
km的路程,那么她走了多长时间?如用字母v表示速度,用字母s表示路程,那么她走的时间又如何表示呢
知2-导
感悟新知
解:小莉走20km所花的时间为20÷5=4(h).
若用字母v表示速度,用字母s表示路程,则时间t=s÷v=
.
从上述例子看到,用字母表示数,可以统一、简明地表示实际问题中的数量关系
知2-讲
感悟新知
总
结
用字母表示日常生活中的数或数量关系,仅仅是把具体数用字母代替了,其实际意义与具体数是一致的,它将个别数量关系转变为一般数量关系.
知2-练
感悟新知
D
A
知3-导
感悟新知
知识点
用字母表示图形关系
3
在100米短跑测试中,小帆、大林和小明所用的时间如下表:
姓名
小帆
大林
小明
成绩/s
16
14.5
15.2
速度/(m/s)
知3-导
感悟新知
(1)请你算出他们每人100米短跑的速度,并将计算结果填入表中.
(2)写出计算速度时所用的公式.
(3)这个公式能用来计算汽车、轮船、飞机在某段匀速行驶过程中的速度吗?
知3-导
感悟新知
如果用s表示路程,t表示所用时间,表示速度,那么这个公式就是
用字母表示数、数量关系以及数学事实,不仅形式简单,而且具有一般性,还便于交流。
知3-练
感悟新知
例
3
如图,有一块长为18m,宽为10m的长方形土地,现将三面留出宽都是x(0(1)菜地的长为___________,
宽为____________;
(2)菜地面积为___________________.
(18-2x)m
(10-x)m
(18-2x)(10-x)m2
知3-练
感悟新知
导引:(1)菜地的长等于长方形土地的长减去小路宽的2倍,菜地的宽等于长方形土地的宽成去小路的宽.(2)菜地的面积等于菜地的长乘菜地的宽.
知3-讲
感悟新知
总
结
用含字母的式子表示图形的面积要注意两点:一是图形的构成;二是选择正确的面积公式我们常用到的几何图形面积公式:长方形面积=长×宽;正方形面积=边长的平方;圆的面积=πr2.
知3-练
感悟新知
1.如图,将边长为3a的正方形沿虚线剪成两个正方形和两个长方形.若拿掉边长为2b的小正方形后,再将剩下的图形拼成一个长方形,则这个长方形较长的边长为( )
A.3a+2b
B.3a+4b
C.6a+2b
D.6a+4b
A
课堂小结
用字母表示数
用字母表示数的特点:
(1)一般性:用字母表示的教与以前学过的数不同,但它又是从具体的教中提炼出来的,可以用字母表示任何数;
(2)普遍性:用字母表示数,关系更简明,更具有普遍性;
(3)在同一个问题中,不同的数量需用不同的字母表示;在不同的问题中,同一个式子或字母可以表示不同的含义.
必做:
请完成教材课后习题
课后作业
作业
第1节
用字母表示数
第二章
代数式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
含字母式子的书写方法
用字母表示数量关系
用字母表示图形关系
课时导入
复习提问
引出问题
科学家爱因斯坦上小学时,在一次数学课中,发现了下列的等式:
1+2-2+1,
3.5+5.6=5.6+3.5,
他认为,这是数的运算的一个重要规律,于是就把这个规律告诉了他的老师和同学,得到了大家的赞赏.
知识点
含字母式子的书写方法
知1-导
感悟新知
1
据中国新闻网2011年9月19日报道:中国工程院院士袁隆平指导的“Y两优2号”百亩超级杂交稻试验田平均亩产926.6
kg,创中国大面积水稻亩产的最高纪录.
知1-导
感悟新知
(1)根据上面数据完成下表:
亩数
1
1.5
2
2.5
3
…
总产量(kg)
926.6×1
926.6×1.5
从表中可知,总产量可用“926.6×亩数”求得.
知1-导
感悟新知
(2)如果用字母a表示亩数,那么a亩水稻的总产量是多少?
(3)如果平均亩产为b
kg,那么a亩水稻的总产量是多少?
a亩水稻的总产量是926.6×a(kg).
平均亩产为bkg时,a亩水稻的总产量是a×b(kg).
知1-导
感悟新知
2011年9月29日
21
时169,我国成功发射了“天官一号”飞行器,它是目前中国最大、最重的在轨飞行航天器.已知“天宫一号”大约每小时绕地球飞行2.844万千米,则它飞行2
h,25
h分别飞行了多少
万千米?如果时间为th,那么它飞
行了多少万千米?
知1-导
感悟新知
“天宫一号”飞行2h,2.5
h分别飞行了(2.844×2)万千米,(2.844×2.5)万千米.
th飞行了2.8441万千米
知1-讲
感悟新知
1.
意义:用表示数的字母表示问题中的数或数量关系;用字母表示数可以统一、简明地表示实际问题中的数量关系.
知1-讲
感悟新知
2.用字母表示数的书写规则:
(1)字母与字母相乘时,“×”通常省略不写或写成“.”;
(2)字母与数字相乘时,数字通常写在字母的前面;
(3)带分数与字母相乘时,通常化带分数为假分数;
(4)字母与字母相除时,要写成分数的形式。
(5)数字与数字相乘,一般仍用“×”号,也可用“.”号,但要注意与小数点分开.
知1-讲
感悟新知
3.易错警示:
(1)同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示;
(2)用字母表示实际问题中的某个量时,字母取值必须使式子有意义且符合实际情况.
知1-讲
感悟新知
例
1
填空:
(1)比a的0.6倍大c的数________;
(2)a与b的2倍的积为________.
0.6a+c
2ab
方法点拨
用字母表示日常生活中的数或数量关系,仅仅是把具体数用字母代替了,其实际意义与具体数是一致的,它将个别数量关系转变为一般数量关系.
知1-讲
总
结
感悟新知
列字母表达式的步骤:
(1)认真审题,将问题中表示数量关系的词语正确地转化为对应的运算;
(2)注意语言所表达的运算顺序,一般“先读先写";
(3)浓缩原题,分段处理,即在比较复杂的语句中,一般会有多个“的”字出现,列式时,可找出各个“的”字将句子分成几段,逐步列出.
知1-练
感悟新知
D
C
知2-导
感悟新知
知识点
用字母表示数量关系
2
①注意字母具有一般性:用字母可以表示我们已经学过的任意一个有理数,同时随着我们所学知识的深入与需要,数的范围将进一步扩大,字母可以表示今后我们所学到的任何一个数.
②注意字母的确定性,它表现在两个方面:一方面是指在同一个问题中,同一个字母只能表示同一个量,不同数量要用不同的字母来表示.另一方面,在用字母表示数时,一旦式子中的字母的取值确定了,式子的值也就随之确定了.
知2-导
感悟新知
③注意字母的不确定性:同一个式子可以表示多种实际问题中的数量关系.
④注意字母的限制性:用字母表示实际问题中的某一个数量时,字母的取值必须使这个问题有意义且符合实际.
⑤注意字母的抽象性:要逐步理解和接受有些问题的结果可能就是一个用字母表示的式子.
知2-导
感悟新知
⑥字母的选择:同一个数量可以用不同的字母表示,同一字母在不同的环境中可以表示不同的数,在同一题中不同的数要用不同的字母表示.
知2-导
感悟新知
例2
2小莉以5km/h的速度,走了20
km的路程,那么她走了多长时间?如用字母v表示速度,用字母s表示路程,那么她走的时间又如何表示呢
知2-导
感悟新知
解:小莉走20km所花的时间为20÷5=4(h).
若用字母v表示速度,用字母s表示路程,则时间t=s÷v=
.
从上述例子看到,用字母表示数,可以统一、简明地表示实际问题中的数量关系
知2-讲
感悟新知
总
结
用字母表示日常生活中的数或数量关系,仅仅是把具体数用字母代替了,其实际意义与具体数是一致的,它将个别数量关系转变为一般数量关系.
知2-练
感悟新知
D
A
知3-导
感悟新知
知识点
用字母表示图形关系
3
在100米短跑测试中,小帆、大林和小明所用的时间如下表:
姓名
小帆
大林
小明
成绩/s
16
14.5
15.2
速度/(m/s)
知3-导
感悟新知
(1)请你算出他们每人100米短跑的速度,并将计算结果填入表中.
(2)写出计算速度时所用的公式.
(3)这个公式能用来计算汽车、轮船、飞机在某段匀速行驶过程中的速度吗?
知3-导
感悟新知
如果用s表示路程,t表示所用时间,表示速度,那么这个公式就是
用字母表示数、数量关系以及数学事实,不仅形式简单,而且具有一般性,还便于交流。
知3-练
感悟新知
例
3
如图,有一块长为18m,宽为10m的长方形土地,现将三面留出宽都是x(0
宽为____________;
(2)菜地面积为___________________.
(18-2x)m
(10-x)m
(18-2x)(10-x)m2
知3-练
感悟新知
导引:(1)菜地的长等于长方形土地的长减去小路宽的2倍,菜地的宽等于长方形土地的宽成去小路的宽.(2)菜地的面积等于菜地的长乘菜地的宽.
知3-讲
感悟新知
总
结
用含字母的式子表示图形的面积要注意两点:一是图形的构成;二是选择正确的面积公式我们常用到的几何图形面积公式:长方形面积=长×宽;正方形面积=边长的平方;圆的面积=πr2.
知3-练
感悟新知
1.如图,将边长为3a的正方形沿虚线剪成两个正方形和两个长方形.若拿掉边长为2b的小正方形后,再将剩下的图形拼成一个长方形,则这个长方形较长的边长为( )
A.3a+2b
B.3a+4b
C.6a+2b
D.6a+4b
A
课堂小结
用字母表示数
用字母表示数的特点:
(1)一般性:用字母表示的教与以前学过的数不同,但它又是从具体的教中提炼出来的,可以用字母表示任何数;
(2)普遍性:用字母表示数,关系更简明,更具有普遍性;
(3)在同一个问题中,不同的数量需用不同的字母表示;在不同的问题中,同一个式子或字母可以表示不同的含义.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
