七年级数学三角形内角和定理课件
文档属性
| 名称 | 七年级数学三角形内角和定理课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 322.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-21 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
数学王子高斯说:“给我最大快乐的,
不是已懂得知识,而是不断的学习;
不是已有的东西,而是不断的获取;
不是已达到的高度,而是继续不断的攀登。”
里辛一中“分层互助”教学学案
知识与技能: 1、掌握三角形的内角和定理的两个推论
及其证明。
2、体会几何关系中不等关系的简单证明。
过程与方法: 3、从内和外、相等和不等的不同角度对
三角形作全面的思考。
情感、态度、 4、通过一题多解,初步体会思维的
价值观 : 多向性,引导学生的个性化发展。
不相邻内角
B
外角
相邻内角
1
A
C
D
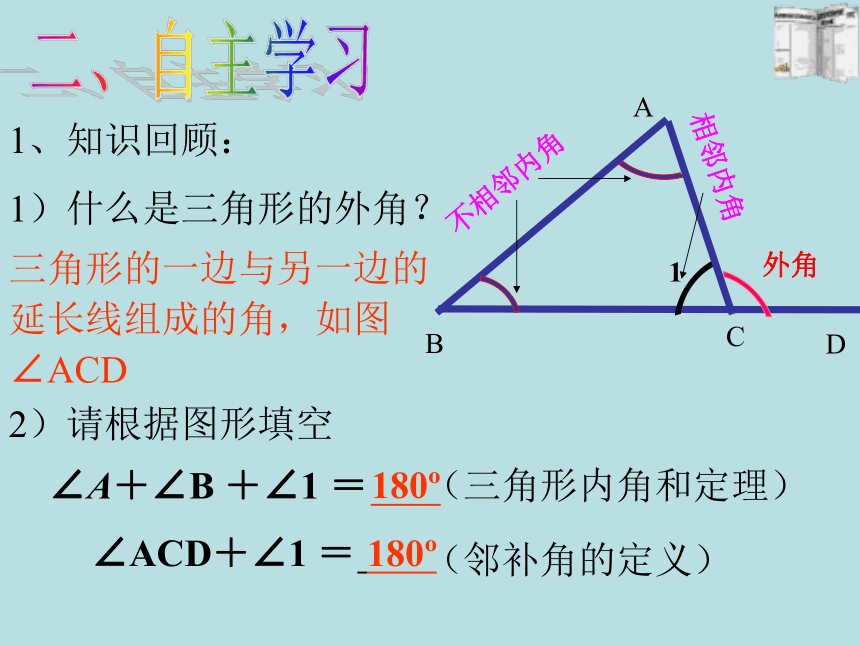
∠A+∠B +∠1 =
∠ACD+∠1 =
180
180
1、知识回顾:
1)什么是三角形的外角?
三角形的一边与另一边的延长线组成的角,如图∠ACD
2)请根据图形填空
(三角形内角和定理)
(邻补角的定义)
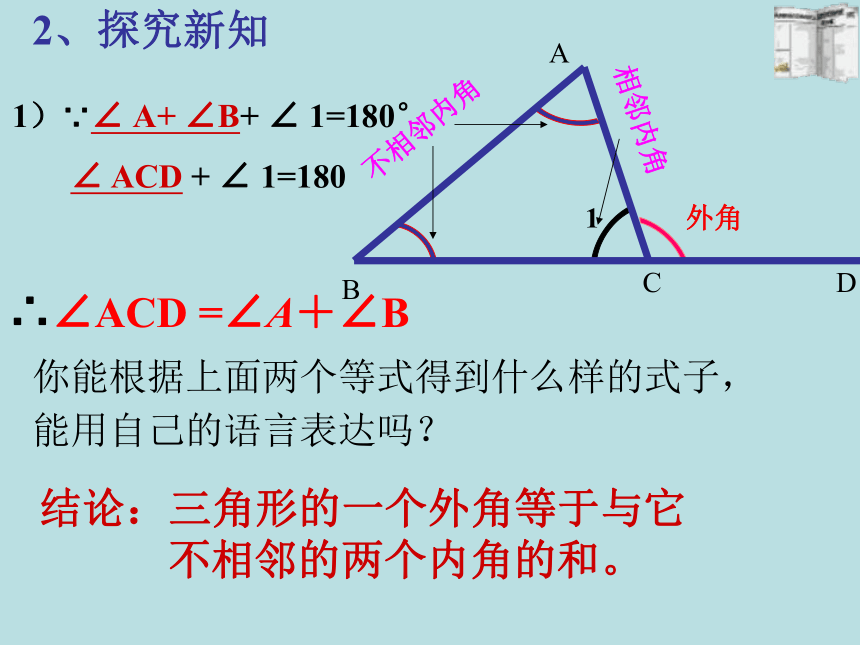
2、探究新知
外角
相邻内角
不相邻内角
1
A
B
C
D
1)∵∠ A+ ∠B+ ∠ 1=180°
∠ ACD + ∠ 1=180
∴∠ACD =∠A+∠B
你能根据上面两个等式得到什么样的式子,
能用自己的语言表达吗?
结论:三角形的一个外角等于与它
不相邻的两个内角的和。
1
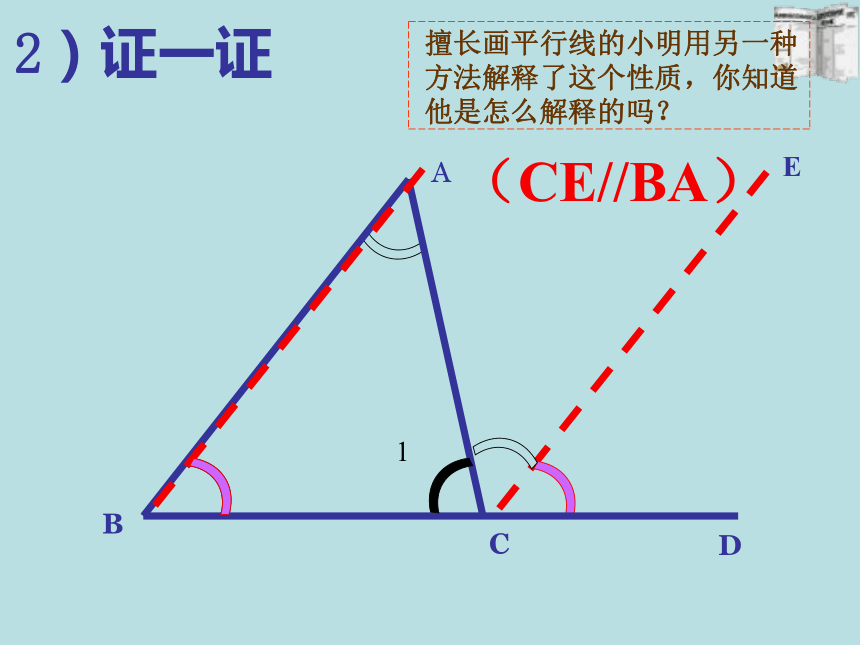
(CE//BA)
A
E
2)证一证
擅长画平行线的小明用另一种方法解释了这个性质,你知道他是怎么解释的吗?
C
B
D
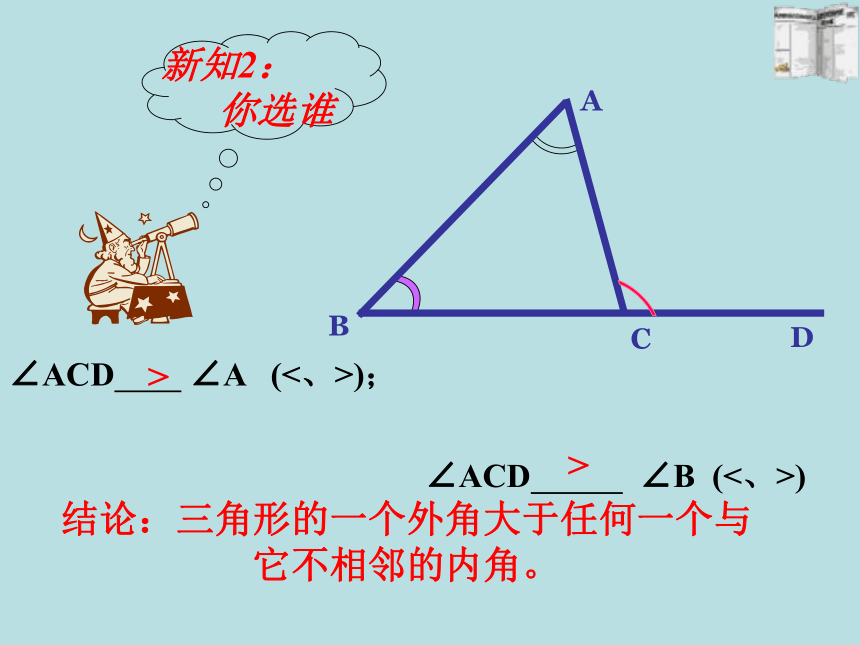
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
新知2:
你选谁
内涵与外延
.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论(corollary).
推论可以当作定理使用.
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
关注▲外角
A
B
C
D
1
2
3
4
这两个结论跟公理和定理一样可以直接运用
35°
120°
1
45°
50°
1
∠1=85°
∠1=95°
3、小试牛刀
B
3
2
1
A
C
D
E
2)把图中∠1、 ∠2、 ∠3
按由大到小的顺序排列
1)
∠1>∠2>∠3
已知:如图6-13,在△ABC中,AD平分外角
∠EAC, ∠B=∠C
求证:AD∥BC.
A
C
D
B
E
运用了定理“内错角相等,两直线平行”得到了证实.
3)现学现用
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∠B=∠C (已知)
∴∠C= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴ AD∥BC(内错角相等,两直线平行).
C B 在一个三角形花坛的外围走一圈,在每一个拐弯
的地方都转了一个角度( ∠ 1, ∠ 2, ∠ 3),
那么回到原来位置时,一共转了几度?
A
B
C
1
2
3
∠1+∠2 +∠3 =
从哪些途径探究这个结果
三角形的外角和360°
(你认识外角吗 )
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
解:过A作AD平行于BC
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAD
所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAD=360°
两直线平行,同位角相等
D
∠2+ ∠ 3= ∠ 4+∠BAD
A
B
C
D
E
F
1
H
2
A 已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
分析:设法利用外角把这五个角“凑”到一个
三角形中,运用三角形内角和定理来求解.
解:∵∠1是△BDF的一个外角(外角的意义),
∴ ∠1=∠B+∠D(三角形的一个外角
等于和它不相邻的两个内角的和).
又∵ ∠2是△EHC的一个外角(外角的意义),
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的
两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和定理).
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
C:1、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
1
2
3
360°
N
P
M
B 2、活学活用
A 4、如图,在△ABC中,AD⊥BC,AE平分 ∠BAC,∠B=80° ∠C=30 °求∠DAE的度数
A
B
C
D
E
1、三角形内角和定理的推论
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360
严格性之于数学家,犹如道德之于人.
由“因”导“果”,执“果”索“因”是探索证明思路最基本的方法.
言必有据,因果对应.是初学证明者谨记和遵循的原则.
下课了!
数学王子高斯说:“给我最大快乐的,
不是已懂得知识,而是不断的学习;
不是已有的东西,而是不断的获取;
不是已达到的高度,而是继续不断的攀登。”
里辛一中“分层互助”教学学案
知识与技能: 1、掌握三角形的内角和定理的两个推论
及其证明。
2、体会几何关系中不等关系的简单证明。
过程与方法: 3、从内和外、相等和不等的不同角度对
三角形作全面的思考。
情感、态度、 4、通过一题多解,初步体会思维的
价值观 : 多向性,引导学生的个性化发展。
不相邻内角
B
外角
相邻内角
1
A
C
D
∠A+∠B +∠1 =
∠ACD+∠1 =
180
180
1、知识回顾:
1)什么是三角形的外角?
三角形的一边与另一边的延长线组成的角,如图∠ACD
2)请根据图形填空
(三角形内角和定理)
(邻补角的定义)
2、探究新知
外角
相邻内角
不相邻内角
1
A
B
C
D
1)∵∠ A+ ∠B+ ∠ 1=180°
∠ ACD + ∠ 1=180
∴∠ACD =∠A+∠B
你能根据上面两个等式得到什么样的式子,
能用自己的语言表达吗?
结论:三角形的一个外角等于与它
不相邻的两个内角的和。
1
(CE//BA)
A
E
2)证一证
擅长画平行线的小明用另一种方法解释了这个性质,你知道他是怎么解释的吗?
C
B
D
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
新知2:
你选谁
内涵与外延
.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论(corollary).
推论可以当作定理使用.
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
关注▲外角
A
B
C
D
1
2
3
4
这两个结论跟公理和定理一样可以直接运用
35°
120°
1
45°
50°
1
∠1=85°
∠1=95°
3、小试牛刀
B
3
2
1
A
C
D
E
2)把图中∠1、 ∠2、 ∠3
按由大到小的顺序排列
1)
∠1>∠2>∠3
已知:如图6-13,在△ABC中,AD平分外角
∠EAC, ∠B=∠C
求证:AD∥BC.
A
C
D
B
E
运用了定理“内错角相等,两直线平行”得到了证实.
3)现学现用
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∠B=∠C (已知)
∴∠C= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴ AD∥BC(内错角相等,两直线平行).
C B 在一个三角形花坛的外围走一圈,在每一个拐弯
的地方都转了一个角度( ∠ 1, ∠ 2, ∠ 3),
那么回到原来位置时,一共转了几度?
A
B
C
1
2
3
∠1+∠2 +∠3 =
从哪些途径探究这个结果
三角形的外角和360°
(你认识外角吗 )
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
解:过A作AD平行于BC
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAD
所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAD=360°
两直线平行,同位角相等
D
∠2+ ∠ 3= ∠ 4+∠BAD
A
B
C
D
E
F
1
H
2
A 已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
分析:设法利用外角把这五个角“凑”到一个
三角形中,运用三角形内角和定理来求解.
解:∵∠1是△BDF的一个外角(外角的意义),
∴ ∠1=∠B+∠D(三角形的一个外角
等于和它不相邻的两个内角的和).
又∵ ∠2是△EHC的一个外角(外角的意义),
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的
两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和定理).
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
C:1、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
∠A+∠B+∠C+∠D+∠E+∠F= .
A
D
E
C
F
B
1
2
3
360°
N
P
M
B 2、活学活用
A 4、如图,在△ABC中,AD⊥BC,AE平分 ∠BAC,∠B=80° ∠C=30 °求∠DAE的度数
A
B
C
D
E
1、三角形内角和定理的推论
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360
严格性之于数学家,犹如道德之于人.
由“因”导“果”,执“果”索“因”是探索证明思路最基本的方法.
言必有据,因果对应.是初学证明者谨记和遵循的原则.
下课了!
